2.3. Проверка гипотез и интервальное оценивание

Проверка гипотез и основанные на них статистические выводы являются одной из важных задач математической статистики.

Существует два подхода проверки гипотез:

1. Классический

2. Подход, основанный на определении уровня вероятности.

Первый подход более ранний и в последнее время используется все реже, второй подход более популярным стал при развитии компьютерной техники.

Статистическая гипотеза рассматривает предположения о величине параметра генеральной совокупности. Процесс проверки гипотез базируется на формировании двух гипотез: нулевая и альтернативная, то есть формируются две конкурирующие гипотезы и проверяется, какая из них является верной.

Нулевая гипотеза (Н₀) – допущение, которое считается верным до тех пор, пока не будет доказана обратная альтернатива, исходя из результатов статистической проверки.

Альтернативная гипотеза (Н₁) – гипотеза, принимаемая, если в результате статистической проверки отвергается Н₀.

Точная формулировка гипотезы зависит от того, что конкретно мы хотим установить. Например, нам нужно проверить и принять решение относительно добросовестности работы продавца какого-либо магазина. Для конкретной проверки выбран фасованный товар (сахар в пакетах весом 1 кг). С точки зрения математической статистики надо проверить гипотезу, которая формулируется следующим образом:

Математическое ожидание веса пакетов генеральной совокупности равно 1 кг. Принять решение нужно на основе имеющегося материала – по взвешенным пакетам.

№ пакета	1	2	3	4	5	6	7	8	9	10
Вес пакета	1,05	0,98	0,96	1,15	1,05	0,89	0,95	1,1	1	1,02

Гипотеза формулируется:

Н₀ (нулевая): М=1; Н₁: М ≠ 1; М₀ = 1

Если мы захотим узнать, превышает ли средний вес пакета 1 кг, то гипотеза записывается следующим образом: Н₀: М = 1 Н₁: М > 1

Для того чтобы проверить гипотезу, необходимо выполнить статистическую проверку, которая состоит из использования стандартизируемого статистического критерия, вычисляемого по данным выборки и используемого для принятия решения или принятия его опровержения относительно выдвинутой гипотезы. Для расчета стандартизированного статистического критерия нужно рассчитать математическое ожидание и дисперсию для нашей выборки.

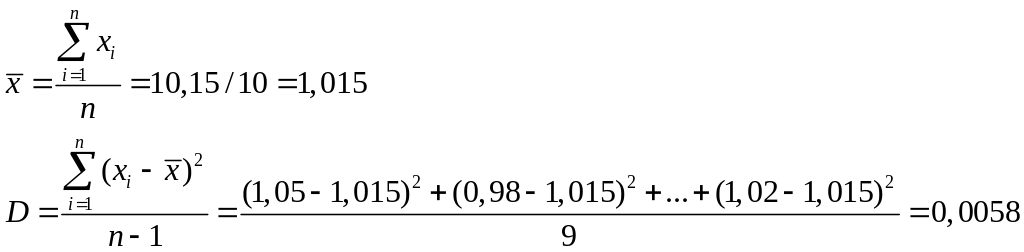Проверим нашу нулевую гипотезу, для этого рассчитаем некоторую статистическую величину по следующей формуле:

; .

М₀ – математическое ожидание для нулевой гипотезы

n – количество наблюдений

t – t–статистика или стандартизированный критерий проверки

t–статистика имеет t – распределение с n–1 степенями свободы. Для t – распределения (распределение Стьюдента) имеются соответствующие таблицы, в которых рассчитано его значение для различных вероятностей и объемов выкладки (n). Эти таблицы называются таблицами квантилей. В Exsel CТЬЮДРАСПОБР(n-1;0,1).Таким образом, величина t подчиняется t – распределению. Его расчетное значение должно лежать в области правдоподобных значений для t – распределения. Следовательно, если мы зададим достаточно большую вероятность и по этой вероятности найдем интервал для t (по таблице квантилей), то этот интервал и будет обладать правдоподобным значением t. Если t расчетное находится в этом интервале, то у нас есть все основания принять нашу Н₀.

t^расч = (1,015-1)/(0,076/10)=1,974

Находим t табличное (t^табл):

, t^расч > t^табл

Расчетное значение t^расч не попадает в область правдоподобных значений. Следовательно, нулевую гипотезу о равенстве математического ожидания 1 кг отвергаем с вероятностью 90 %, то есть в 90 случаях из 100 вес пакета ≠ 1 кг.

Формально классическая процедура проверки гипотезы может быть выражена следующей схемой:

1. Вычисляется оценка вероятностной характеристики показателей выборочной информации.

2. Выдвигается гипотеза о равенстве оценки, полученной по выборочной информации истинному значению вероятностной характеристики генеральной совокупности.

3. Вычисляется некоторая статистика по полученной выборке. Эта статистика должна подчиняться одному из известных законов распределения вероятностей.

4. Задав достаточно большую вероятность, находим по таблице распределения интервал для правдоподобных значений, вычисленных статистикой. Значение задаваемой вероятности называется статистической надежностью.

5. Если числовое значение расчетной статистики попадает в полученный интервал, то Н₀ гипотезу принимаем, в противном случае – отвергаем.