1.3.2. Примеры законов распределения

1 пример.

Равномерное распределение:

п лотность f(x)

а в

2 пример.

Нормальное распределение так же называют распределением Гаусса – Лапласа. Распределение вероятностей случайной непрерывной величины х называется нормальным, если ее закон распределения вероятностей определяется плотностью вероятности.

плотность причем М (х) =а (математическое ожидание)

среднее квадратичное отклонение

Д(х)= дисперсия.

3 пример.

Распределение χ² с п степенями свободы.

χ²=

Где ε₁,…… ε_n – независимые стандартные нормальные случайные величины, т.е. .

4 пример.

Распределение Стьюдента (t –распределение с n- степенями свободы). Пусть ε_0, ε_1,…… ε_n независимые случайные переменные.

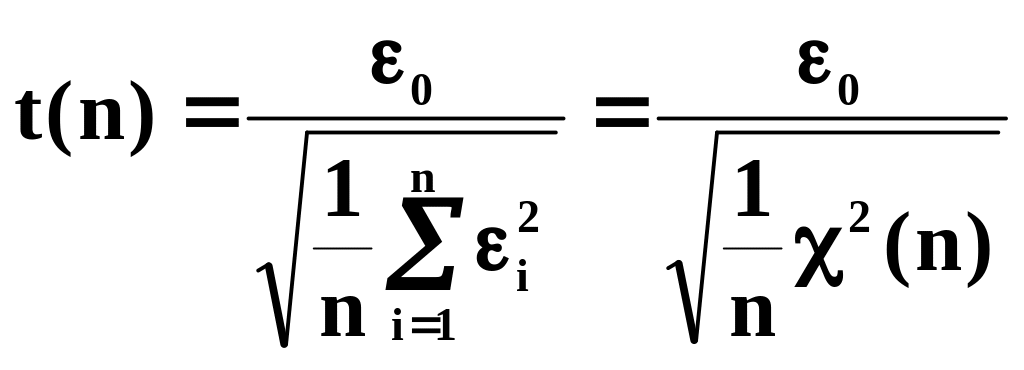- называют распределением Стьюдента или t –распределением с n степенями свободы.

5 пример.

Распределение Фишера (распределение F, Фишера – Спенсера).

Пусть ε₁,……, ε_m,, η₁,….,. η_n -совокупность независимых стандартных нормальных случайных величин.

Распределение случайной величины с (m, n) степенями свободы.

1.3.3. Математическое ожидание

Математическое ожидание.

для дискретных для непрерывных

где х_i- дискретная величина; х – непрерывная величина;

p_i- ее вероятность; f(x)- плотность вероятности.

Свойства математического ожидания:

Пусть х,у - произвольные случайные величины, а и в- const, тогда

1⁰. М (а)=а

2⁰. М (ах+в) = а М(х) +в

3⁰. М (х+у) = М(х) + М(у)

4⁰. М (х у) = М (х) * М(у)

5⁰. х у, то М(х) М(у)

1.3.4. Дисперсия случайной величины

Дисперсия случайной величины отражает степень разброса случайной величины относительно среднего значения. Для дискретной величины

D(x)= M (x-M(x))² = [ M(x) – x_i]² P_i

Дисперсия непрерывной случайной переменной

D (x)= [M (x)- x]² f(x) dx

Дисперсия имеет следующие свойства:

1⁰ D(a)=0, а – любое число

2⁰ D (ax+b)= a² D(x)

3⁰ D (x+y)= D(x)+D(y)

4⁰ D(x)= M(x²)- (M(x))²

1.3.5. Многомерное распределение вероятности

Понятие условного распределения вероятности возникает в задачах, в которых требуется выяснить распределение вероятности одной переменной при фиксированных значениях другой. Распределение, которое характеризует плотность вероятности разных значений х₁, при условии, что х₂ – известно и принимает фиксированные значения, называется условным распределением.

Функция условной плотности вероятностей определяется как отношение двух плотностей:

, f₂(х₂)0 – плотность вероятности х₁ при фиксированном значении х₂.

Плотность вероятности х₂, при фиксированном значении х₁: , f₁(х₁)0

Математическое ожидание х₁ при заданном значении х₂ определяется по формуле: