4.5. Нелинейные регрессионные модели (нрм).

Рассмотрим из всех видов нелинейных моделей класс линеализируемых, то есть моделей, приводящихся к линейному виду с помощью тех или иных преобразований:

1. Полином k-той степени имеет вид y= b₀+b₁x+b₂x²+b₃x³+…+b_kx^k. Данное уравнение приводят к линейному виду путем замены x = X₁, х² = X₂, x³ = X₃,…, x^k = X_k. В результате мы имеем многофакторное линейное регрессионное уравнение

y=b₀ + b₁ X₁ + b₂ X₂ + b₃ X₃ +…+ b_k X_k.

2. Гиперболическая функция имеет уравнение вида y=a+b/x. Произведем линеаризацию модели путем замены Х=1/x, в результате получим линейное уравнение: y=a+bХ.

3. Уравнение степенной модели имеет вид: у=aх^b. Произведем линеаризацию модели, для этого произведем логарифмирование обеих частей уравнения: lgy=lga+b*lgx. Обозначим Y= lgy, X= lgx, A= lga, Тогда уравнение примет вид линейного уравнения: Y=A+bХ.

4. Уравнение показательной функции имеет вид: у=ab^x. Произведем линеаризацию модели, для этого произведем логарифмирование обеих частей уравнения: lgy=lga+x*lgb. Обозначим Y= lgy, A= lga, , B= lgb, Х=х. Тогда уравнение примет вид линейного уравнения: Y=A+BХ.

5. Показательная функции вида: у=aе^bx. Произведем линеаризацию модели, для этого произведем логарифмирование обеих частей уравнения по натуральной основе: lny=lna+bx. Обозначим Y= lny, A= lna. Тогда уравнение примет вид линейного уравнения: Y=A+bx.

Приведенные примеры не исчерпывают класс линеализируемых функций. Аналогичным образом могут быть линеаризируемы другие функции, при этом после линеаризации функция должна иметь вид линейной модели относительно коэффициентов уравнения.

4.6. Использование регрессионных моделей для прогнозирования.

Регрессионные уравнения используются для решения многих задач экономических исследований. Наиболее важной из них является прогнозирование. После получения удовлетворительных регрессионных уравнений прогнозирование осуществляется довольно просто, а именно, путем подстановки в регрессионное уравнение прогнозного значения аргумента или аргументов, то есть прогнозные значения у определяются следующим образом:

y_прог=f (х_прог)

Таким образом, основная проблема прогнозирования сводится к получению моделей, адекватных исследуемым эконометрическим процессам. Подробного изучения требует вероятность надежности прогнозов, это в свою очередь сводится к проблеме построения доверительных интервалов прогноза.

Построение доверительных интервалов прогноза для однофакторного регрессионного уравнения опирается на оценку дисперсии ошибки прогноза , которая оценивается следующим образом:

где х_прог - значение аргумента, для которого определяется прогноз,

² – остаточная дисперсия уравнения регрессии.

Зная можно построить доверительный интервал для истинного значения прогноза y_прог с заданной вероятностью. Для этого воспользуемся обстоятельством, что t-статистика подчиняется t-распределению с n-2 степенями свободы.

при этом

у_прог – оценка прогноза на основе уравнения регрессии.

Таким образом, с заданной вероятностью р величина находится в интервале:

; .

Отсюда интервал для истинного значения прогноза будет иметь следующий вид:

.Ширина доверительного интервала зависит от:

1. С ростом остаточной дисперсии регрессионного уравнения ширина доверительного интервала прогноза увеличивается, то есть, чем точнее качество подгонки регрессионного уравнения, тем надежнее прогноз.

2. С расширением выборки (с ростом количества наблюдений – n) доверительный интервал прогноза сужается, то есть, чем больше информации используется в предпрогнозных исследованиях, тем точнее будет прогноз.

3. С удалением прогнозного значения аргумента от среднего значения выборки, ширина доверительного интервала увеличивается. Это происходит, потому что с отдалением прогнозного значения неопределенность прогнозного периода растет.

4. Ширина доверительного интервала прогноза зависит также от значения t^табл ( ), которое в свою очередь зависит от количества уровней ряда и уровня вероятности причем, при росте вероятности значение t^табл при прочих равных условиях растет, следовательно, с ростом вероятности доверительный интервал прогноза расширяется.

Для многофакторной линейной регрессионной модели Y=b₀+b₁X¹+b₂X²+…b_kX^k

Доверительный интервал прогноза будет иметь следующие границы:

Верхняя граница прогноза: Y_пр+U.

Нижняя граница прогноза: Y_пр-U.

,
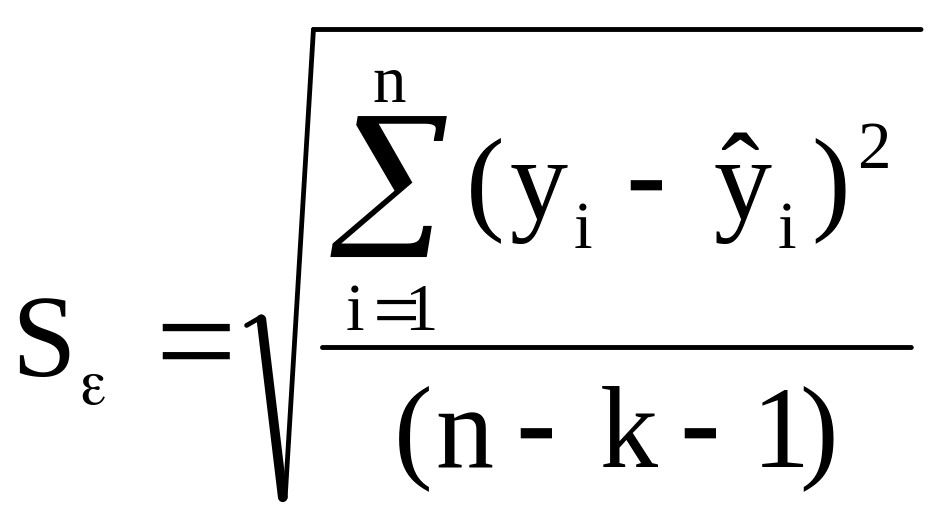