2.3.2 Проверочный расчет вала приводного колеса по эквивалентным нагрузкам

Определяем нагрузки, действующие на вал.

Из кинематической схемы привода видим, что вращательный момент на приводном валу примерно (без учета потерь в муфтах) равен вращательному моменту на выходном валу редуктора, то есть:

.

Трение качения не учитываем.

Определим окружную силу на колесе:

, (7)

где – крутящий момент в опасном сечении выходного конца вала,

– окружная сила на колесе, Н;

– диаметр беговой дорожки, м.

Из формулы (7) находим окружную силу:

(Н).

Примем рациональную нагрузку равной окружной силе , т.е. Н.

Составим расчетную схему вала.

Расчетная схема вала

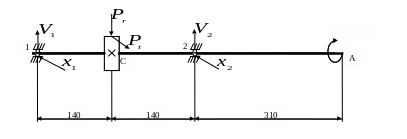
Рисунок 5

2.3.3 Определяем опорные реакции вала

а) вертикальная плоскость.

Анализируем характер нагрузки: вал загружен в вертикальной плоскости радиальной силой с колесом;

Вес муфты и вала не учитываем, т.к. они малы по сравнению с приложенной нагрузкой. Значит опорные реакции равны полу сумме приложенной нагрузки, т.к. приложена симметрично относительно опор.

Находим реакции в вертикальной плоскости:

, (8)

б) горизонтальная плоскость.

В горизонтальной плоскости на вал через колесо действует окружная сила , причем она приложена симметрично относительно опор.

Следовательно, опорные реакции и равны между собой, т.е.:

, (9)

(Н).

2.3.4 Построение эпюр изгибающих моментов

Расчет ведем по характерным сечениям:

а) в вертикальной плоскости находим моменты относительно оси «х»:

При и , .

б) в горизонтальной плоскости находим моменты относительно оси «y»:

При и , =

По найденным значениям, построим две эпюры изгибающих моментов в горизонтальной и вертикальной плоскостях.

2.3.5 Расчет и построение эпюры крутящих моментов

Крутящий момент в сечениях участка вала А-С равен:

.

На участке вала С-1 крутящий момент равен нулю.

По найденным значениям строим эпюру крутящих моментов для участка вала А-1 (смотри рисунок 6).

Эпюра крутящих моментов

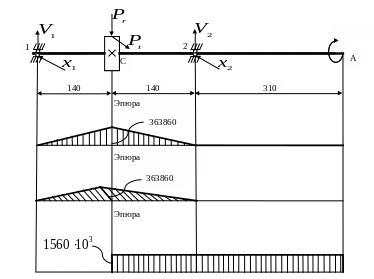
Рисунок 6

2.3.6 Проверка прочности вала по эквивалентным нагрузкам

Рассчитываем эквивалентные нагрузки вала:

, (10)

где – расчетное эквивалентное напряжение в опасном сечении вала, МПа;

– расчетный эквивалентный момент в опасном сечении вала, ;

– полярный момент сопротивления, ;

– допускаемое напряжение, МПа.

Допускаемое напряжение для данной марки стали составляет 40÷33,3 МПа.

Принимаем МПа.

, (11)

где d – диаметр вала в исследуемом сечении, мм.

Из уравнения (10), и учитывая формулу (11), получим:

. (12)

Определяем эквивалентный момент в опасном сечении вала (сечение «С») по третьей теории прочности:

, (13)

( ).

Тогда расчетный диаметр вала в опасном сечении должен быть:

(мм).

Сравнивая с чертежом, видим, что номинальный диаметр d = 130 мм, следовательно, условие прочности соблюдается.