11.Отклик измерительной системы.
Реакция ИС на приложенное ко входу воздействие называется откликом системы. Отклик ИС должен давать верное представление о воздействии. Когда значения измеряемых физических величин меняются со временем (то есть в случае, когда измеряют динамические величины), важно точно знать, как ИС будет отслеживать эти изменения: поведение системы в динамике должно обеспечивать верное воспроизведение измеряемой величины.
Динамические свойства линейной ИС целиком определяются ее откликом на единичный скачок на входе (ее переходной характеристикой). Зная переходную характеристику можно найти время установления или время считывания ИС. (Исследования во временной области) рис…..
Динамическое
поведение линейной ИС также целиком
определено, если известно, как она
реагирует на синусоидальное колебание
меняющейся частоты; т.е. в том случае,
когда мы знаем частотную характеристику.
Поведение линейной системы полностью
определяется АЧХ
и ФЧХ
.
Характеристикой частотных свойств
служит ширина полосы пропускания
(граничная частота
,
на которой мощность выходного сигнала
падает вдвое, по сравнению с максимальной
мощностью на входе). На частоте
амплитуда выходного сигнала уменьшается
в
раз (-3дб).
Соотношение между входной величиной x(t) и выходной величиной y(t) , а значит, и динамическое поведение линейной динамической системы можно представить в виде линейного дифференциального уравнения. Если y зависит от x , то дифф. уравнение, описывающее соотношение между y и x , содержит не только функции от y и x , но также и производные по времени от этих функций. В линейном дифференциальном уравнении имеются только такие члены, в которых функция y и ее производные входят в первой степени. Порядок дифференциального уравнения равен наивысшему из порядков входящих в него производных.
У многих ИС, различных по своей природе (электрических, тепловых, механических,…), динамическое поведение оказывается сходным. Если описывать эти системы в обобщенном виде в терминах U- и I-величин, то мы будем получать одни и те же дифференциальные уравнения. С точки зрения динамического поведения особенно важным является порядок дифференциального уравнения. С учетом этого говорят об ИС n-го порядка и об отклике n-го порядка, если поведение системы можно описать с помощью дифференциального уравнения n-го порядка.
На практике большинство ИС можно с достаточной точностью описать линейным дифференциальным уравнением второго или более низкого порядка (0,1,2).
Системы нулевого порядка.
Дифференциальное
уравнение, описывающее систему нулевого
порядка, является лишь простым
алгебраическим уравнением. Система
является статической
или, говоря другими словами,
частотно-независимой.
Пример:
потенциометрический преобразователь
смещения (рис….). В этом датчике смещение
х преобразуется в пропорциональное ему
выходное напряжений U. Пусть при х=0
сопротивление между нижним концом
потенциометра и движком равно
, а максимальное сопротивление при
равно
;
тогда связь между выходным напряжением
U и смещением х можно представить:
.
Это частный случай уравнения вида:
y=ax+b.
Здесь b либо имеет
нулевое значение, либо играет роль
начального смещения, а a—чувствительность.
Время установления
равно нулю, а ширина полосы--
.
Это конечно же идеализация (таких систем
нет), но в том диапазоне частот, который
существенен при измерении данной
величины, систему можно считать мгновенной
(система квази-нулевого порядка).
Пример2: Датчик Холла (рис….)
,
где
--выходное
напряжение датчика Холла;
--постоянная
Холла для данной пластины;
t—толщина пластины;
--ток
,протекающий по пластине;
B—индукция магнитного поля;
--начальное
смещение.
Датчик удобен при измерении больших токов (не нужно разрывать цепь).
Системы первого порядка.
Уравнение преобразования таких систем—линейное дифференциальное уравнение первого порядка.
А) Анализ во временной области.
Пример1. RC-цепь
(интегрирующая цепочка). Рис. ….
Пусть
и
--входное
и выходное напряжения.
;
,
тогда
.
Полагая RC=
,
уравнение можно представить в виде
(*). Здесь
,
а
.
Это уравнение решается просто. При скачкообразном входном сигнале
при
;
при
,
А выходной сигнал
(переходная характеристика
)находим из
,
или в операторной форме
,
откуда
.
Общее решение
имеет вид:
.
Частным решением
при
(при этом емкость С зарядится до величины
)
является функция
(установившееся значение):
Полагая, что
при
,
найдем переходную характеристику:
.
Здесь
установившееся
значение, а
-постоянная
времени.
Если относительная
погрешность ИС не может превосходить
,
то время установления равно:
;
;
.
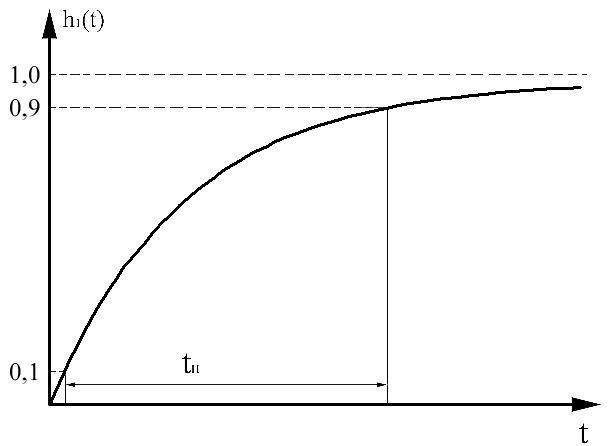
Рис. Переходная характеристика системы первого порядка.
Если необходимо
иметь малую ошибку
, то время установления может оказаться
очень большим. Это является недостатком
ИС, описываемых дифференциальными
уравнениями первого порядка.
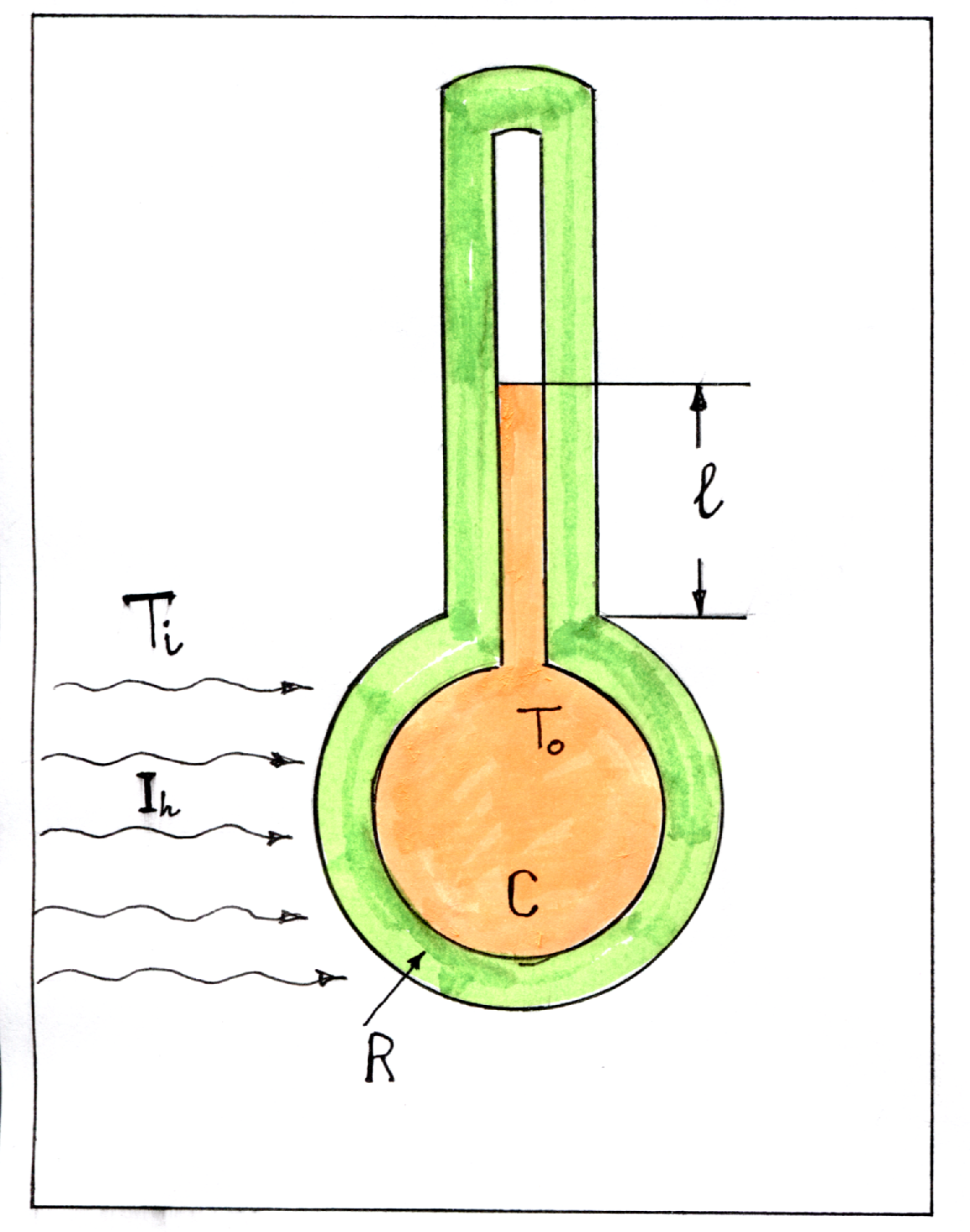
Пример2. Ртутный термометр.
Изменение длины
столбика ртути (определяемое по
откалиброванной шкале—выходной сигнал)
прямо пропорционально изменению
температуры ртути в резервуаре термометра
. Входной сигнал—измеряемая температура
окружающей среды
.
Для описания динамического поведения
термометра можно принять температуру
ртути в резервуаре за выходную величину.
Теплообмен между
ртутью в резервуаре и окружающей средой
должен происходить через стеклянную
стенку с тепловым сопротивлением R.
Тепловую емкость (теплоемкость) ртути
в резервуаре обозначим C. Поток тепла
(эквивалентен электрическому току в
RC-цепи)
.
Для малого приращения тепла
получим:
.
Кроме того,
,
поэтому
;
;
;
.
Вводя RC= , приходим к уравнению (*).
.
Б) Анализ в частотной области.
Частотная
характеристика—это, по существу, отклик
системы на синусоидальный входной
сигнал
в установившемся режиме, то есть отклик,
спустя длительное время после включения
сигнала и подачи его на вход, когда все
переходные явления затухнут. Частотную
характеристику находят как частное
решение дифференциального уравнения,
описывающего систему первого порядка,
при
.
Частотную характеристику легко получить, применяя комплексные переменные в электрическом аналоге системы первого порядка (рис….,RC-цепочка).
Получим:
, где
.
Модуль
равен
,
а аргумент имеет вид
.
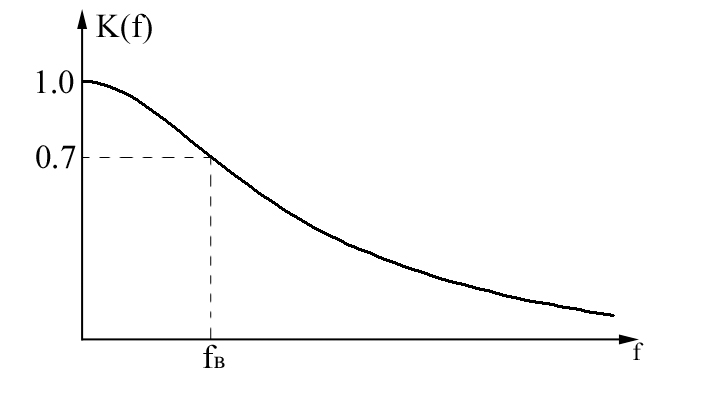
АЧХ и ФЧХ RC-цепи представлены на рис…..
|
|
|
Граничная частота
находится из условия
,
и равна
Измерительные системы второго порядка.
У измерительных систем второго порядка соотношение между входным сигналом и выходным сигналом выражается линейным дифференциальным уравнением второго порядка.
Рассмотрим динамические свойства магнитоэлектрического ЭМП. Его измерительный механизм представляет собой вращающуюся механическую систему. Каждая из следующих четырех механических пар сил оказывает воздействие на вращающуюся часть измерителя, создавая вращающий момент.
Отклоняющее воздействие. Это воздействие вызывает отклонение стрелки на угол θ. Момент этого воздействия пропорционален измеряемой величине (току)--
.Возвращающее воздействие. Это воздействие оказывает противодействие отклонению стрелки (противодействующий момент)-
.
В установившемся режиме
.
Противодействующий момент пропорционален
углу отклонения стрелки θ, т.е.
θ,
где
-коэффициент
упругости (жесткость пружины) или
удельный противодействующий моментДемпфирующее воздействие. Оно также противодействует отклоняющему воздействию. Демпфирующий момент пропорционален угловой скорости стрелки:
,
где
-постоянная
затухания вращающейся конструкции.
Затухание линейно зависит от угловой
скорости
.
Применяют воздушное демпфирование
(поршни, крыльчатки), а также индукцию
вихревых токов в подвижной металлической
пластине.Инерционность. Инерция вращающейся конструкции измерителя приводит к возникновению еще одного противодействующего момента, который пропорционален угловому ускорению стрелки:
,
где
-момент
инерции вращающейся конструкции
относительно оси вращения.
Таким образом, динамическое поведение измерителя определяется его уравнением движения ; в любой момент времени отклоняющий момент уравновешивается суммой всех других моментов:
,
или
.
Мы пришли к линейному дифференциальному уравнению второго порядка.
Введем новую
переменную
:
.
Это уравнение справедливо для различных систем. Здесь отклоняющий момент является I-величиной, а угловая скорость --U-величиной (таблица 1). Для механической системы с поступательным движением:
.
Обе механические ИС аналогичны электрической системе—параллельному контуру. Для электрической системы (параллельный колебательный контур) мы определяем U- величину, являющуюся решением уравнения:
.
Это уравнение
эквивалентно полученным ранее. Различие
может состоять в том, что I-
величины и U-
величины поменяются местами. Структура
системы остается одной и той же, когда
мы переходим от J
к m
или C
, одновременно заменяя
на
или
, а также
на
или
.
(обращаем внимание: во всех рассматриваемых ИС токовая величина (выходная) связана с величиной U (входной) через интегральное соотношение; т.е. в установившемся режиме все три линейные ИС являются интеграторами. Эту особенность линейных ИС первого порядка мы отмечали при анализе уравнения преобразования магнитоэлектрического прибора).
Полагая
,
получаем
,
Где I представляет собой ток, текущий по катушке L.
Дифференциальное уравнение, описывающее линейную систему второго порядка , в общем случае содержит две постоянные a и b:
.
Здесь х—это величина входного воздействия x(t), а y—выходная величина y(t), нормализованная по отношению к чувствительности по постоянному току S(0), так, что y=y(t)/S(0).
Для большей
наглядности, введем две другие постоянные:
относительное затухание z
и угловую частоту
свободных незатухающих колебаний в
системе:
.
Для системы с вращением:
.
Для системы с поступательным движением:
.
Для электрической цепи:
.
Соответствующее уравнение в операторной форме имеет вид:
.
Его корни равны:
.
Различают три характерных случая:
1.
--недостаточное
демпфирование.
При подаче на вход
единичного скачка, на выходе возникают
затухающие колебания с частотой
,
наложенные на конечное значение (рис.
..). С ростом z
затухание колебаний происходит все
быстрее, поэтому z
называют относительной
скоростью затухания.
При z=0
колебания непрерывны с частотой
.
2. z=1—критическое демпфирование.
Конечное значение
,
как и ранее, равно
,
но при этом на выходе затухающие колебания
отсутствуют.
Измерительные
механизмы с подвижной катушкой
конструируют так, чтобы
,
при этом в таких приборах происходит
небольшое проскакивание стрелки (4%), но
удобнее наблюдать установление стрелки.
В электрических системах в этом случае
АЧХ оказывается горизонтальной в
наиболее широком диапазоне частот.
3.
--избыточное
демпфирование,
при этом выходная величина будет
постепенно приближаться к конечному
значению
.
Лекция: Источники ошибок.
Введение.
Судьбоносные ошибки и просчеты великих ученых:
Одна из серьезных причин, почему немцы не создали свою атомную бомбу – ошибочные эксперименты известного немецкого физика – В. Боте.
В январе 1941 года на основе своих исследований Боте приходит к заключению, что паразитное поглощение нейтронов графитом недопустимо велико, а потому графит нельзя использовать в реакторе в качестве замедлителя нейтронов. Авторитет Боте был столь велик, что результаты никто не оспаривал. Ставку немцы сделали на тяжелую воду, но…Единственный в мире завод по производству тяжелой воды был в Норвегии. Стабильные поставки срывали патриоты Норвегии. А в результате действий антифашистов в 1944 году был потоплен паром с 10-ю тоннами тяжелой воды. Это сорвало все сроки исследовательских работ немецких физиков.
2. Ошибочный эксперимент, вернее отрицательный результат в эксперименте американского физика Майкельсона: при попытках прямым способом измерить скорость движения Земли относительно «эфира» с помощью изобретенного им интерферометра Майкельсон получил нулевой результат. В результате он стал первым физиком, получившим Нобелевскую премию, а Эйнштейн получил экспериментальное подтверждение своей теории относительности
Под помехой понимается сигнал, однородный с измерительным и действующий одновременно с ним: u(t) = uc(t) + un(t). Его присутствие приводит к появлению погрешности измерения.
Имея представление об источниках помех, экспериментатор получает возможность их уменьшения. Вообще искусство экспериментатора во много определяется его умением определять источники помех и находить пути повышения точности эксперимента. В конечном счете источники помех – это источники ошибок при эксперименте.
Источники возможных ошибок могут быть проиллюстрированы по следующей обобщенной схеме :
Рис. 1
Первый источник ошибок измерения – обратное влияние измерительной системы на объект измерения, приводящее к изменению измеряемой величины:
Примеры:
Влияние входного сопротивления СИ (анэнергетическое согласование);
Влияние отражения сигнала (энергетическое согласование).
Второй источник ошибок обусловлен взаимодействием между выходом измерительной системы и наблюдателем.
«Наблюдателем» может быть человек или регистрирующее устройство (самописец, цифровой регистратор и т.п.).
Обратное влияние наблюдателя на И.С. также приводит к ошибкам измерения.
Примеры:
Считывание показаний стрелочного прибора под углом, а не по направлению, перпендикулярному к шкале прибора (ошибка параллакса);
Нагружающее действие входного импеданса регистратора на выходные каскады И.С.
Третий источник ошибок.
Измерительная система находится в двухсторонней связи с окружающей средой. Окружающая среда может существенно влиять на результат измерения: «возмущающее» воздействие.
Примеры:
Аддитивные и мультипликативные помехи (термоэлектричество, токи утечки, индуктивные и емкостные наводки помехи и др.).
Четвертым источником ошибок измерения являются несовершенные характеристики СИ.
Рассмотрим природу перечисленных источников ошибок измерения и способы снижения величины этих ошибок.