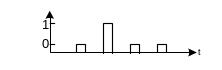3.Отклик ис на форму сигнала (чувствительность к форме сигнала).

Измерительный сигнал—сигнал, содержащий количественную информацию об измеряемой физической величине. Отклик ИС на входной сигнал в общем случае зависит от формы (вида или структуры) этого входного сигнала.

3.1 Классификация сигналов.

Измерительный сигнал – сигнал, содержащий количественную информацию об измеряемой физической величины.

Измерительные сигналы чрезвычайно разнообразны. Их можно классифицировать по различным признакам.

• По характеру информативного и временного параметров сигналы делятся на:

- Аналоговые

- Дискретные

- Цифровые

• По характеру изменения во времени:

- Постоянные; - Переменные

• По степени наличия априорной информации:

- Детерминированные; - Квазидетерминированные;

- Случайные

Аналоговый сигнал - сигнал, описываемый непрерывной или кусочно непрерывной функцией Y(t) (рис.3.1а).

Дискретный сигнал – сигнал, изменяющийся дискретно по времени или по уровню (рис.3.1в,с). В первом случае он принимает любые значения (отсчеты) в дискретные моменты времени nt (рис.3.1в). Во втором – принимает ограниченный ряд значений S_i = nq

(q-квант) в любой момент времени tÎ(t_мин; t_макс) (рис.3.1с).

Цифровые сигналы – квантованные по уровню и дискретные по времени сигналы (рис.3.1d). Уровням квантования S₁,S₂,S₃ …присваивается цифровой код (см. раздел 3.4).

а) b)

c) d)

Рис.3.1

а) - аналоговый, с) – дискретный по уровню (квантованный),

b) – дискретный по времени, d) – квантовано-дискретизованный сигнал.

Постоянные сигналы – их значение с течение времени не меняется; переменные сигналы – значения которых меняются во времени.

Переменные сигналы могут быть непрерывными (их параметры изменяются непрерывно) и импульсными - сигналами конечной, сосредоточенной на небольшом временном интервале времени, энергии.

Детерминированные сигнал ( математическая модель) – сигнал, закон изменения которого известен, а модель не содержит неизвестных параметров.

Квазидетерминированные сигналы – сигналы с частично известным характером изменения во времени (один или несколько параметров – неизвестны).

Подавляющее число измерительных сигналов являются квазидетерминированными. Например, при снятии амплитудно-частотных характеристик усилителя, мы подаем на вход синусоидальный сигнал с известными параметрами (форма –sin, амплитуда -U _, частота -f_о), а на выходе получаем сигнал с неизвестной амплитудой U .

В амплитуде синусоидального сигнала U содержится измерительная информация о коэффициенте передачи усилителя на данной частоте f_o:

К_х (f_о) =

Детерминированные и квазидетерминированные сигналы могут быть периодическими (мгновенные значения меняются через Т – период) и непериодические (однократные импульсные сигналы).

Случайные сигналы - это изменяющаяся во времени физическая величина, мгновенные значения которой являются случайной величиной.

3.2. Математическое описание сигналов. Параметры измерительных сигналов.

В метрологии измерительные сигналы описываются математическими моделями вида: Y = f (Х,а,в,с…), где

Y - основной информационный параметр сигнала;

Х – независимый аргумент;

а,в.с,… - параметры сигнала.

В зависимости от рода независимого аргумента (время – t, или частота – ), сигналы описываются временными (х = t) или частотными (х = ) математическими моделями.

Вид модели определяется условием метрологической задачи.

Временная область.

Y = F (t; а, в, с…) – временное представление сигналов. Применяют при расчетах, когда один (или несколько) из параметров а, в, с…зависит от измеряемой величины.

Частотная область.

Y = F ( ; а, в, с) – частотное (спектральное) представление сигналов позволяет оценить его частотный диапазон. Это важная характеристика сигнала, позволяющая определить необходимую полосу пропускания средства измерения для передачи сигналов с требуемой точностью.

Простейшим видом периодического сигнала является синусоидальный (гармонический) измерительный сигнал.

Y (t) = Y_м sin ( t + Y _м sin (2 ft + ) (3.1)

Параметрами сигнала являются:

• Амплитуда Y ;

• Частота f (или период Т = ) ;

• Начальная фаза .

Рис. 3.2 Спектр гармонического сигнала.

График временной модели – общеизвестен. А график частотной модели (спектр), представлен на рис.3.2

Любые другие периодические сигналы являются полигармоническими, спектр которых состоит из множества гармонических сигналов. Их частотное представление основывается на преобразовании Фурье:

Y(t) = А_о + (3.2), где:

Ао – постоянная составляющая; А_n, - амплитуда и фаза n – ой гармоники.

А_n ( ) и ( ) – образуют амплитудный и фазовый спектры, которые характеризуют свойства сигнала Y(t) в частотной области (рис. 3.3)

а) б)

Рис.3.3

Амплитудный (а) и фазовый (б) дискретные спектры.

Спектральное представление сигнала позволяет оценить его частотный диапазон, т.е. граничные частоты, между которыми заключены все или основные, имеющие наибольшие амплитуды, гармоники сигнала.

Для того, чтобы правильно выбрать средство измерений (например, вольтметр, осциллограф), экспериментатор должен уметь оценить частотный спектр исследуемого сигнала и его допустимые искажения и, таким образом, определить верхнюю граничную частоту f_гр или полосу пропускания необходимого СИ.

Эта задача всегда встает перед экспериментатором, потому что периодические функции, выбранные в качестве математической модели сложного сигнала, имеют бесконечный спектр (f_в ), а любое реальное измерительное устройство имеет всегда ограниченную полосу пропускания с f_гр (рис. 3.4).

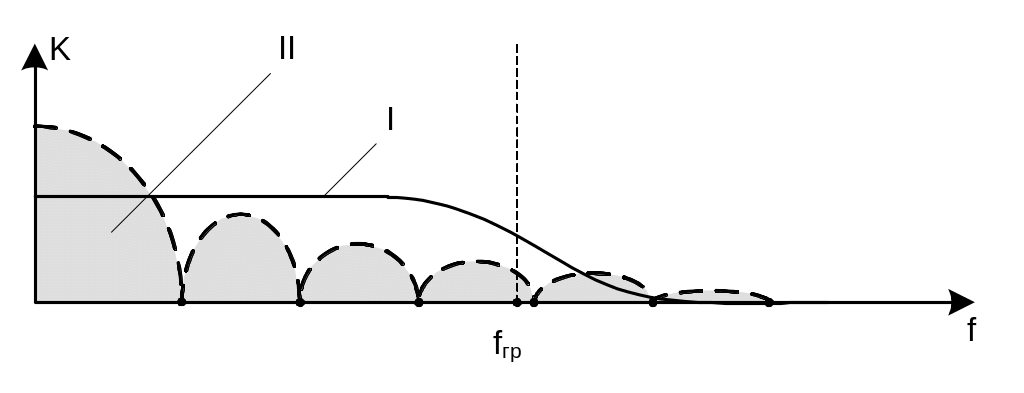
Рис. 3.4 Амплитудно-частотная (I) характеристика СИ и спектр периодической последовательности прямоугольных импульсов (II).

Через СИ с АЧХ (I) с полосой пропускания O – f_гр пройдут только гармоники этого диапазона, в результате сигнал будет искажен (потеряны верхние гармоники: f_гр - ).

Прямое и обратное преобразования Фурье позволяют оценить искажения сигнала (изменение его формы), обусловленные ограничением спектра и, тем самым, по допустимым искажениям экспериментатор может правильно выбрать СИ по его граничной частоте f_гр.

Этот параметр всегда приводится в нормативно технических характеристиках таких приборов, как осциллограф, вольтметр и т.п.

Пример: Оценить нижнюю f_м и верхнюю f_в частоты полосы пропускания осциллографа, используемого для исследования 3-х сигналов одинаковой частоты f_о и амплитуды U_м: синусоидального, линейного знакопеременного (рис.3.5 а) и знакопеременного меандра (рис.3.5 б).

Рис. 3.5 Линейный знакопеременный (а) сигнал и сигнал «меандр» (б)

Математические модели сигналов:

u₁(t) = U_мsin(2πft) – синусоидальный сигнал

4 U_м t/T при t [0; T/4]

u₂(t) = 4 U_м (T/4-t)/ T+ U_м при t [T/4; 3T/4] - Линейный знакопеременный сигнал

4 U_м (t-3T/4)/ T- U_м при t [ 3T/4; T]

U_м при t [0; T/2]

u₂(t) = - «Меандр»

-U_м при t [T/2; Т]

Определим спектральный состав измеряемых сигналов, разложив их в ряд Фурье:

u₁(t) = U_м sinωt;

u₂(t) = 4 U_м /π (sinωt – 1/9 sin3ωt + 1/25 sin5ωt – 1/49 sin7ωt + …);

u₃(t) = 4 U_м /π (sinωt + 1/3 sin3ωt + 1/5 sin5ωt – 1/7 sin7ωt + …).

Отсюда видно, что спектры сигналов u₂(t) и u₃(t) – бесконечны.

Принимаем следующее условие: для внесения минимальных искажений в форму сигнала канал осциллографа должен пропускать все гармоники, амплитуда которых составляет более 1% относительно первой гармоники (U ).

Спектры сигналов u₂(t) и u₃(t) содержат только нечетные гармоники, но их амплитуды затухают с разной интенсивностью:

• Для сигнала u₂(t) – пропорционально 1/n²;

• Для сигнала u₃(t) – пропорционально , где n – номер гармоники.

Номер гармоники u₂(t), после которой их амплитуда <0,01U_м, равен 11 (100/11² = 0,83%), для u₃(t) соответственно 101 (100/101 = 0.99%).

Таким образом, при синусоидальном сигнале u₁(t) граничная частота осциллографа f_гр должна быть больше частоты сигнала f_о , при сигнале типа u₂(t) - f_гр 11 f_о; а при исследовании сигнала u₃(t) - f_гр 101 f_о.

Например: f_о = 100кГц

Тогда для исследования сигнала u₃(t) - «меандр» с допустимыми искажениями за счет СИ, граничная частота осциллографа должна быть . Этому условию удовлетворяет осциллограф С1-93 у которого f_гр = 20мГц.

Переменный периодический сигнал Y(t) кроме совокупности мгновенных значений, описывается так называемыми интегральными параметрами. Эти параметры характеризуют вид (форму) сигнала и особое значение имеют для экспериментатора, когда возникает необходимость измерения среднеквадратического значения напряжения сложного сигнала вольтметром, градуированным в действующих значениях синусоидального напряжения.

Интегральные параметры периодического сигнала:

Амплитудное (пиковое) значение Y_м равно максимальному на периоде значению сигнала.

Среднее значение (постоянная составляющая) сигнала: (3.3)

Средневыпрямленное значение сигнала:

(3.4)

Среднеквадратическое значение сигнала:

; (3.5)

где Y_к – среднеквадратическое значение к ^ой гармоники. Среднеквадратическое значение сигнала является единственной истинной мерой его мощности. В связи с этим, подавляющее большинство вольтметров проградуированы в среднеквадратических значениях напряжения.

Связь между этими параметрами устанавливается с помощью коэффициентов:

k_a = - коэффициент амплитуды (3.6)

k_ф = - коэффициент формы (3.7)

k_у = - коэффициент усреднения. (3.8)

Пример:

Определить интегральные параметры и k_a, k_ф, k_у для сигнала пилообразной формы.

u(t) = U_м при tÎ[О, Т]

Решение.

U_ср=U_срв=

U_скз = U =

k_a = k_ф = ; k_у = k_a k_ф = 2

Легко показать, что для сигнала «меандр»

k_a = k_ф = k_у = 1,

а для синусоидального сигнала соотношения известны: U= , U_cрв =

отсюда: k_a = ; k_ф = ; k_у =

3.3. Дискретные сигналы.

Прямоугольные импульсы.

Частным случаем дискретных сигналов являются прямоугольные импульсы и их последовательность. В электро - радиотехнических устройствах широкое применение находят сигналы прямоугольной формы (одиночные или их периодическая последовательность). Измерительная информация может быть заложена как в параметр такого сигнала (длительность t_u, амплитуда U_м, длительность фронта t_ф) так и в наличие или в отсутствие импульса (кодовый сигнал).

В связи с этим импульсные сигналы прямоугольной формы характеризуются некоторыми специфическими параметрами и их искажениями. Прямоугольный импульс характеризуется

ΔU

параметрами: (математическая модель)

U_м – амплитуда

t_u - длительность

Рис. 3.6

I – идеальный прямоугольный импульс

II – реальный (с искажениями) импульс

Параметры и искажения реального импульса:

• Амплитуда – установившееся значение - U_м¢

• Длительность - t_u¢ на уровне 0,5 U_м

• Длительность переднего фронта (0,1¸0,9)U_м = t_ф

• Длительность заднего фронта (спад импульса) (0,9¸0,1)U_м = t_сп

• Выброс - d

Искажения прямоугольного сигнала (импульса) обусловлены конечной граничной частотой измерительных устройств (фронты t_ф и t_сп), а также типом, вернее порядком частотных характеристик измерительных систем (выброс «d»).

Периодическая последовательность прямоугольных импульсов характеризуется скважностью q:

3.4. Цифровые сигналы.

Сигналы, дискретизованные по времени и квантованные по уровню, в которых мгновенное значение в каждый момент времени kDt кодируется соответствующим кодом, называются цифровыми.

В этих сигналах информация заложена не в значении (например, напряжение) сигнала в данной точке измерения (kt), а числе импульсов и их взаимном расположении (рис. 3.7; табл.1).

Рис. 3.7. Аналоговый (1) и дискретизованно-квантованный (2) сигналы.

Таблица 1

	Значение напряжения, Ui , В	Цифровой сигнал , Uц (t)
U1	1
U2	3
U3	2
U4	1
U5	2
U6	4
U7	5

На рисунке и в таблице 5.1 показан принцип преобразования непрерывного сигнала (1) в дискретно-квантованный, а затем в двоичный 4-х разрядный код – цифровой сигнал.

Таким образом, главным отличием цифрового сигнала является то, что измерительная информация заложена не в значении параметра, а в различении – обнаружении или необнаружении его в заданные моменты времени (нет – «0», есть – «1»). Это принципиальное отличие, т.к. неточности измерительного канала, помехи, шумы, приводящие к появлению погрешностей при измерении значения параметра сигнала, практически не влияют на различение (обнаружение: да-нет) цифрового сигнала.

Значения «0» и «1» по напряжению отличаются в несколько раз и простое пороговое устройство легко различает эти сигналы, даже если на них наложена помеха.

К недостаткам цифрового сигнала относится то, что его спектр значительно шире (а значит, он требует более широкой полосы пропускания измерительных систем), чем у аналогового сигнала, из которого он сформирован.

Пример. Рассмотрим ширину спектра звукового сигнала в телефонии, преобразованного в цифровой сигнал.

В телефонии официально введена полоса пропускания канала с f_гр = 3,4 кГц, что существенно меньше спектра звукового сигнала (f_гр ~ 20 кГц). Это сделано в целях экономии (при этом в одной линии связи можно разместить больше каналов). Речь человека при этом вполне разборчива.

Перейдем к цифровому сигналу.

1. Частота дискретизации: f_д =

2. Зададим квант изменения сигнала:

q = DU = 1 мВ

3. Динамический диапазон звукового речевого сигнала (U_мин ¸U_макс) составляет

30 ¸ 35 дб, т. е. Д = дб.

Это соответствует 30 шагам квантования, т.е. U_мин = 1мВ; U_макс = 30мВ.

4. Для передачи одного отсчета (1 двоичного кода) с таким диапазоном необходимо

log₂ 30 @ разрядов двоичного числа., т.е. 5 бит информации (N).

При частоте дискретизации 6,8 кГц, скорость передачи информации будет равна :

C = f_д × N = 6,8 кГц × 5 = 34 кГц.

Мы видим, что ширина спектра цифрового сигнала в телефонии (простейший сигнал) в 10 раз больше аналогового. Это плата за качество (чистота звука, без помех) и точность воспроизведения сигнала.

В общем случае, скорость передачи в бит/с равна:

С = 2F_в log₂N,

Где: F_в – верхняя частота спектра сигнала;

N – число уровней квантования.