ФПК-2013г. Раздел 1. Основы метрологии.

Предмет метрологии

Метрологи—наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности (ГОСТ 16263-70

« ГСИ. Метрология, Термины и определения».

(metron-мера, logos-учение).

Метрология делится на три раздела:

• Теоретическая метрология- в ней излагаются общие вопросы теории измерений;

• Прикладная метрология — изучает вопросы практического применения в различных сферах деятельности результатов теоретических исследований;

• Законодательная метрология — рассматривает комплексы взаимосвязанных общих правил, требований и норм.

Предметом метрологии является извлечение количественной информации о свойствах объектов и процессов с заданной точностью и достоверностью.

Средства метрологии — это совокупность средств измерений и метрологических стандартов, обеспечивающих их рациональное использование.

Понятие о единстве измерений.

Под единством измерений понимается характеристика качества измерений, заключающаяся в том, что их результаты выражаются в узаконенных единицах (1), размеры которых в установленных пределах равны размерам воспроизведенных величин (2), а погрешности результатов измерений известны с заданной вероятностью и не выходят за установленные пределы (3). Это понятие охватывает важнейшие задачи метрологии: унификацию единиц ФВ, разработку систем воспроизведения и передачи их размеров рабочим СИ с установленной точностью и ряд других вопросов. На достижение и поддержание на должном уровне единства измерений направлена деятельность государственных и ведомственных метрологических служб, проводимая в соответствии с установленными правилами, требованиями и нормами. На государственном уровне деятельность по обеспечению единства измерений регламентируется стандартами Государственной системы обеспечения единства измерений (ГСИ) или нормативными документами органов метрологических службы.

Для обеспечения единства измерений необходима тождественность единиц, в которых проградуированы все существующие СИ одной и той же величины. Это достигается путем точного воспроизведения и хранения в специализированных учреждениях установленных единиц ФВ и передачи из размеров применяемым СИ.

Воспроизведение единицы ФВ--это совокупность операций по материализации единиц ФВ с наивысшей в стране точностью посредством государственного эталона или исходного образцового СИ.

Передача размера единицы--это приведение размера единицы ФВ, хранимой поверяемым СИ, к размеру единицы, воспроизводимой или хранимой эталоном, осуществляемое при их поверке или калибровке. Размер единицы передается "сверху вниз".

Постулаты теории измерений.

Метрология строится на основе ряда основополагающих постулатов, описывающих ее исходные аксиомы.

Постулат 1. в рамках принятой модели объекта исследования существует определенная измеряемая физическая величина и ее истинное значение.

Пример: деталь--цилиндр: - диаметр - ФВ, может быть измерена;

если эллипс- диаметр не существует.

Измеряемая величина существует лишь в рамках принятой модели. Но данному объекту могут быть сопоставлены различные модели.

Следствие: - для данной ФВ объекта измерения существует множество измеряемых величин (и соответственно их истинных значений).

Данная модель в течении времени, необходимого для измерения, должна позволять считать ее параметр неизменным, отсюда:

Постулат 2.-истинное значение измеряемой ФВ постоянно.

Выделив постоянный параметр модели, можно перейти к измерению соответствующей ФВ.

Для переменной ФВ необходимо выбрать некий постоянный параметр и измерить его (пример: среднеквадратическое или средневыпрямленное значение):

Следствие:- для измерения переменной ФВ необходимо определить ее постоянный параметр—измеряемую величину.

Постулат 3.-существует несоответствие измеряемой величины исследуемому свойству объекта (пороговой несоответствие измеряемой величины).

Пороговое несоответствие—несоответствие между параметром модели и реальным свойством объекта. Оно принципиально ограничивает достижимую точность измерений:

Следствие 1.-истинное значение измеряемой величины отыскать невозможно.

Следствие 2.-достижимая точность измерения определяется априорной информацией об объекте измерения.

История науки и метрологии.

Основоположниками европейской науки принято считать древних греков.

Начало науки как таковой было положено греком—Фалесом Милетским

( ~ 600лет до н.э.).С его именем связывают почти невозможное число открытий. Его захватывающее достижение—предсказание затмения 585 г. до н.э.

Любопытство олицетворяет одно из самых прекрасных свойств человеческого разума—желания знать!

В новом представлении греческих мыслителей, после эры греческих мифов, ( начиная с Фалеса Милетского) Вселенная стала представляться машиной, управляемой непреклонными законами. Греки были преисполнены ощущением, что природные законы могут быть постижимы. Этот греческий оптимизм никогда не покидал человечество! Греки назвали свой метод изучения ФИЛОСОФИЕЙ— «любовью к мудрости» ( желанием знать). До сих пор названия многих физических величин, эффектов, научных терминов взято из греческого языка.

Греки были поклонниками метода познания под названием « дедукция» ( от общего к частному). Этот метод познания , благодаря таким гигантам , как Евклид, Архимед, Аристотель, был главенствующим почти 2000 лет!

Аристотель (384—322г.г. до н.э.)—упорядоченно записал все древние знания. Его логические рассуждения показали, что Земля круглая; в результате была создана мировая система, которая была неверной, но могла бы оказаться в высшей степени плодотворной, если бы последующие поколения не восхищались им так рабски.

Евклид (~300 лет до н.э.)— создатель евклидовой геометрии. Его учебник , в котором были сведены в единую систему все известные теоремы и аксиомы, просуществовал и имел непререкаемый авторитет ~2000 лет!

Архимед (287—212 г.г. до н.э.)— греческий математик. Считается величайшим математиком и инженером древности. Открыл законы рычага и плавучести. Вычислил довольно точно значение с помощью процесса исчерпывания, и при этом чуть было не изобрел дифференциальное и интегральное исчисление.

С помощью линейки и циркуля Архимед пытался найти наиболее точное значение отношения длины окружности к диаметру (число ). Строя внутри окружности вписанные многоугольники и каждый раз удваивая число их сторон, Архимеду хватило времени и терпения достигнуть числа сторон многоугольника, равного 96. При этом он получил , что больше точного значения всего на 0.0082%. Ничего лучшего не удавалось получить в Европе, по крайней мере до XVI века. (почти 1800лет!)

Первые несколько столетий благодаря методу дедукции были достигнуты впечатляющие результаты. Наиболее блестящие результаты были получены в геометрии, особенно в изучении пропорций. Пифагор из Самоса в 525 году до н.э. вывел «теорему Пифагора»: (!).

Вклад греков в геометрию состоял в ее идеализации и абстрагировании. Они считали, что рассмотрение природы и соотношений свойств, присущих математическим числам, позволяют человеку ближе всего подойти к ощущению сути красоты и божественности.

Греками было выведено правило « Золотого сечения».

Под критерием красоты подразумевается внутреннее совершенство и изящество теоретических построений.

Можно привести много примеров, подтверждающих это утверждение.

В основе таких шедевров архитектуры, как Соборы (Киевская София, Московский Кремль, Звонницы Новгорода, Ростова Великого и мн. других) лежит Закон «Золотого сечения».

Хорошо и образно сказал о наших предках, создавших эти шедевры древнерусского зодчества, поэт начала ХХ в. Осип Мандельштам: «Красота – не хитрость полубога, а хищный глазомер простого столяра».

Астроном Кеплер назвал Золотое сечение одним из сокровищ геометрии. В эпоху Возрождения утверждали, что Золотое сечение – это «объединение совершенного разума и абсолютной красоты».

Они были влюблены лишь в заманчивую игру под названием «дедукция». Дедукция—наиболее приемлемое средство достижения знаний! Практические знания-- это нечто низменное. Даже великий Архимед отказался писать (публиковать) о своих практических изобретениях; он распространял только свои достижения в теоретической математике.

Греки возвели аксиомы в ранг «абсолютной истины» и предположили, что другие отрасли знания могли быть развиты от подобной «абсолютной истины».

Так например в астрономии они, как аксиомы, приняли понятия:

• Земля неподвижна— центр Вселенной;

• Все небесные тела вращаются вокруг Земли по кругу, т. к. круг— совершенная кривая и т. д.

В физике: Аристотель разработал фантастические теории движения, исходя из самоочевидных для него аксиом (…скорость падающего тела пропорциональна его весу, и др.).

Вторая серьезная ошибка греков—сосредоточенность на абстрактном и формальном, завела со временем науку вообще в тупик.

Поклонение дедукции с самоочевидными аксиомами привело древних мыслителей к краю пропасти. После того, как греки разработали все значения аксиом, а в дальнейшем сделали важные открытия в математике и астрономии, уже не возникало ни каких вопросов. Все открыто!

Философские знания казались полными и точными почти 2000 лет («Аристотель утверждает», ….»Евклид полагает»..).

Решив проблемы математики и астрономии, греки обратились к более тонким областям знания. Человеческая душа была одной из таких областей.

На передний край науки вышла этика. В качестве высшего этика Греции Платон заменил высшего физика Аристотеля. С 200г. до н.э. до 1200 гг. н.э. европейцы интересовались почти только этикой ( особенно в связи с богословием). Физика была почти позабыта!

Существует очень старый рассказ о том, как молодому М. Планку его учитель говорил: «Физика практически вся закончена, есть только два облачка на ее ясном горизонте: одно – опыт Майкельсона, другое – трудности теории теплового излучения».

Как теперь известно, одно облачко родило теорию относительности, а второе – при решающем участии Планка – привело к созданию квантовой теории.

И только мыслители Ренессанса открыли новую перспективу греческой физики. Это началось с Коперника, но его система не стала переворотом в науке (ученые ее не приняли). Настоящий переворот осуществил итальянец Галилео Галилей!

Он ввел в науку более логичный метод—индукцию. Ее приверженцы начинают исследования с наблюдений (экспериментов) и на их основе делают обобщения. При этом считается очевидным, что ни одному обобщению не будет позволено остаться без изменений, если оно еще хотя бы раз не подтвердится новыми экспериментами. Это краеугольный камень современной физики.

В работе «О движении» (1590) Галилео Галилей подверг критике аристотелевское учение о падении тел. В ней, между прочим, он писал: «Если разум и опыт в чем-нибудь совпадают, для меня не играет роли то, что это противоречит мнению большинства».

Это, пожалуй, первое признание факта, породившего знаменитый афоризм: «Практика является критерием истины».

Важным этапом в развитии европейской науки стало «внедрение» арабских цифр и заслуга в этом принадлежит знаменитому итальянскому математику Фибоначчи.

Леонардо Фибоначчи— самый заметный математик Средневековья. Где-то около 1200г., когда Фибоначчи был в расцвете сил, а крупный торговый город Пиза имел связи с маврами в Северной Африке, Леонардо имел возможность побывать там и воспользоваться плодами мавританского просвещения. К тому времени мусульманский мир принял новую систему написания цифр, позаимствованную от индусов. Фибоначчи изложил ее в книге «Liber Abaci» , опубликованной в 1202году, представил эти «арабские цифры» и подарил их Европе, которая все еще стонала от варварства римских цифр. «Поскольку арабские цифры всего примерно в триллион раз полезнее римских, то понадобилась всего пара веков, чтобы убедить европейских купцов пойти на это изменение».

В той же книге Фибоначчи поставил и решил следующую, ставшую знаменитой, задачу:

Сколько кроликов можно произвести от одной пары в течение года, если каждый месяц каждая пара рождает новую пару, которая со второго месяца своей жизни становится продуктивной, а смерти отсутствуют?

Вот эта последовательность цифр: 1,1,2,3,5,8,13,21,34,55,……144.

Это-последовательность (ряд) Фибоначчи.

Оказалось, что эта последовательность имеет удивительные свойства и имеет весьма важные практические применения:

Описывает кумулятивный рост ;

Описывает распределение листьев на растущей ветке, чешуек на сосновой шишке, семечек в корзинке подсолнуха и т.п.

Последовательность Фибоначчи также оказалась связанной с «золотым сечением», которое важно для искусства и эстетики, а не только для математики!

Отношение предыдущего числа к последующему приближается к значению 0.618 –знаменитое отношение «золотого сечения»!

Но ведь греки знали это отношение ещё до Фибоначчи. Откуда?

Вспомним «Фауста» Гете:

«Мефистофель: Нет, трудновато выйти мне теперь.

Тут кое-что мешает мне немного:

Волшебный знак у вашего порога.

Фауст: Не пентаграмма-ль этому виной?»

(Перевод Б.Пастернака).

Пентаграмма – это пятиконечная звезда. Она служит примером «золотого сечения, которым геометры и строители пользовались с незапамятных времен. Эту же пропорцию мы имеем в ряду Фабиначчи.

Пропорции золотого сечения можно определить

из чертежа пятиконечной звезды, это, по-видимому, было найдено интуитивно. Эту пропорцию легко определить из уравнения:

=

; ;

либо из ряда Фабиначи:

(1; 2; 3; 5; 8; 13; 21; 34; 55;…), (~ 0,618) Или системы размеров Корбюзье «Модулор»

(…; 698; 432; 268; 165; 102; 63; 39; 24; 15; 9; 6 см…) (~ 0,619)

Совершенно неожиданное использование пропорции «золотого сечения» применил архитектор Корбюзье.

В 80-е годы прошлого столетия во ВНИИЭФе (как и в ряде других фирм) появилась система автоматизации научного эксперимента «КАМАК». Построена она по принципу конструктора, состоящего из стандартных блоков – функциональных узлов разного назначения (измерительных усилителей, АЦП, ЦАП, ОЗУ и т.п.). Экспериментатор, подбирая необходимые ФУ, мог создавать автоматизированный измерительный комплекс под различные задачи. Но головной болью для конструкторов стало то, что размеры блоков давались в дюймах!

(Кстати, США до сих пор придерживаются дюймовой системой единиц, теряя на этом десятки миллиардов долларов).

И вот всемирно известный французский архитектор Корбюзье решился на довольно трудную задачу: согласовать метрическую систему с дюймовой. Так появилась система размеров «МОДУЛОР». «Это измерительный прибор, - поясняет автор, - в основе которого лежат человеческий рост и математика».

(дюймовая система, как известно, базируется на размерах частей человеческого тела).

В основу «МОДУЛОРА» положены рост человека, равный 1.829 м, и золотое сечение. Исходная единица закономерно увеличивается или уменьшается последовательно с коэффициентом, равным пропорции золотого сечения: 698; 432; 268; 165; 102; 63; 39; 24; 15; 9 см и т.д.

Размеры «МОДУЛОРА» одинаково хорошо укладываются как в метрическую систему, так и в систему футов.

МЕТРИЧЕСКАЯ СИСТЕМА.

Сегодня в подавляющем большинстве стран мира принята метрическая система физических единиц. В 2010г на эту систему перешла Англия. Парадоксальным является факт, что передовая в техническом отношении страна США до сих пор пользуется старой, ненаучной дюймовой системой мер. Потери США на международном рынке от применения отсталой системы составляют порядка 20 млрд долларов в год!

Ценность М.С.—это логическая система. Ее единицы разумно связаны друг с другом. Все остальные наборы единиц используют отдельные названия для каждой единицы, относящейся к данному типу величин ( мили, футы, дюймы,…;

унции, фунты, граны,… ). Это как у эскимосов: несколько десятков слов для

различного состояния снега ( рыхлый, плотный, когда снег падает, когда он лег,

и т. д.). В нашем языке для этого используется сочетание прилагательного и существительного: влажный снег, плотный снег, рыхлый снег и т. д.. При этом

такие же прилагательные могут использоваться с другими существительными.

Например: жесткий бетон; жесткое мясо; жесткая постель и т. д. Здесь прилагательное ( жесткий) является обобщающим словом.

Метрическая система единиц—единственная система, которая поднялась до этой ступени!

Метрическую систему создали французские ученые в 1795 году.

ПРИМЕР: Величина длины—метр (metrum –лат.; metron –греч. измерять).

Это общий термин длины ( физическая единица). Дифференцируем единицы длины с помощью прилагательных. В метрической системе прилагательные присоединяют к общему слову ( термину), превращая их в приставку ( префикс).

Приставки используют греческие или латинские. При этом , как правило, греческие слова используют для крупных единиц, а латынь—для мелких.

ПРИМЕР: 1000—хилион (кило); 100—гекатон (гекто); 10—дека

0.1—децем; 0.01—сентум (санти); 0.001—милле (милли).

1 километр =1000 метров

1 гектометр =100 метров

1 декаметр = 10 метров

1 метр = 1 метр

1 дециметр= 0.1 метра

1 сантиметр= 0.01 метра

1 миллмметр=0.001 метра

Не имеет значения, какой длины выбран метр—все остальные ( кратные) длины определены! Благодаря тому, что все остальные единицы различаются как степень 10, легко превращать одни единицы в другие. А попробуйте быстро ответить: сколько дюймов в миле?

К сожалению, французские ученые в своей системе не пошли за отметку—тысяча! Им казалось, что 1000 –это уж очень много, а 0.001 –чрезвычайно маленькая для практики величина. Таким образом они ограничились всего шестью порядками: 0.001—1000.

Так как развитие измерительной аппаратуры продвигало науку к самому крупному и самому мелкому практически во всех областях измерений, систему необходимо было расширить!

Чтобы и здесь навести порядок, в 1958 году Международный комитет мер и весов в Париже принял расширенную систему префиксов с интервалом в 3 порядка. Названия префиксов были заимствованы из греческого языка.

Триллион ( )—Тера (teras-чудовище)

Миллиард ( ) – Гига ( gigas-гигант )

Миллион ( ) -- Мега (megas-огромный)

Тысячные ( )—милли

Миллионные ( ) –микро (micros-маленький)

Миллиардный ( )—нано (nanos-карлик)

Триллионный ( )—пико

Итого 24 порядка!

В 1962году добавлены еще два префикса:

Фемто --

Атто --

В результате получили диапазон величин в 30 порядков !

Однако сегодня мы оперируем размерами величин до 83-х порядков!

Раздел 2: Физические свойства и величины.

Все объекты окружающего мира характеризуются своими свойствами. Свойство--категория качественная. Для количественного описания различных свойств объекта вводится понятие величины. Бесконечное многообразие свойств физических объектов затрудняет их отражение совокупностями чисел с ограниченной разрядностью, возникающее при их измерении. Н.Р.Кэмпбелл предложил использовать постулаты математической логики для описания трех наиболее общих проявлений свойств в отношениях эквивалентности, порядка и аддитивности.

В настоящее время основополагающим понятием метрологии, позволяющим количественно или каким-либо другим способом определить свойство объекта, становится понятие "ШКАЛА ИЗМЕРЕНИЙ". Мы привыкли связывать измерение с количественными проявлениями свойств исследуемых явлений, выражаемых единицами физических величин. Долгое время основным содержанием метрологии были такие понятия, как: физические величины, системы физических величин и т.д. По мере развития метрологии наблюдается тенденция рассматривать в качестве объектов исследований все новые, и не только физические, свойства и соответствующие им величины. Так, например, формируется метрологический подход к изучению и описанию свойств биологических, психологических, социальных (в т. ч. экономических) систем.

Шкалами измерений человечество, зачастую не осознавая этого, начало пользоваться очень и очень давно. По видимому уже тогда, когда люди научились пользоваться понятиями «больше», «меньше», «равно», «похоже».

Однако официальная метрология долгое время занималась простыми, устоявшимися измерениями геометрических и механических величин и не ощущала потребности в развитии теории шкал измерений. Ведь главным для развивающейся науки (да и производства) было ЧИСЛО (цифровой результат, получаемый в измерительном эксперименте).

Положение изменилось в середине двадцатого века, когда в сферу интересов метрологии стали входить не только количественные, но и качественные свойства окружающих нас объектов и явлений.

Но только в последние 10-15 лет основные положения теории шкал измерений стали активно использоваться в метрологической теории и практике.

В результате все более значимым в метрологии становится понятие "ШКАЛА ИЗМЕРЕНИЙ". Шкала измерений является более общим понятием, чем единица физической величины, отсутствующая в некоторых видах измерений. Шкалы измерений необходимы как для количественных (длина, температуpa, масса, …), так и для качественных (цвет, вкус, компетенция, …) проявлений свойств объектов (тел, веществ, явлений, процессов).

Проявления свойства объекта образуют множество, элементы которого находятся в определенных логических отношениях между собой, то есть являются так называемой системой с отношениями. Имеются в виду отношения типа "эквивалентность" (равенство); "больше", "меньше" (порядок); возможность "суммирования" элементов или "деления" одного на другой (аддитивность).

Вот Н.Р. Кэмпбелл и предложил использовать постулаты математической логики для описания этих трех наиболее общих проявлений свойств в отношениях эквивалентности, порядка и аддитивности.

МНОЖЕСТВА ПРОЯВЛЕНИЙ СВОЙСТВ ОБЪЕКТОВ

Отношения эквивалентности (шкалы

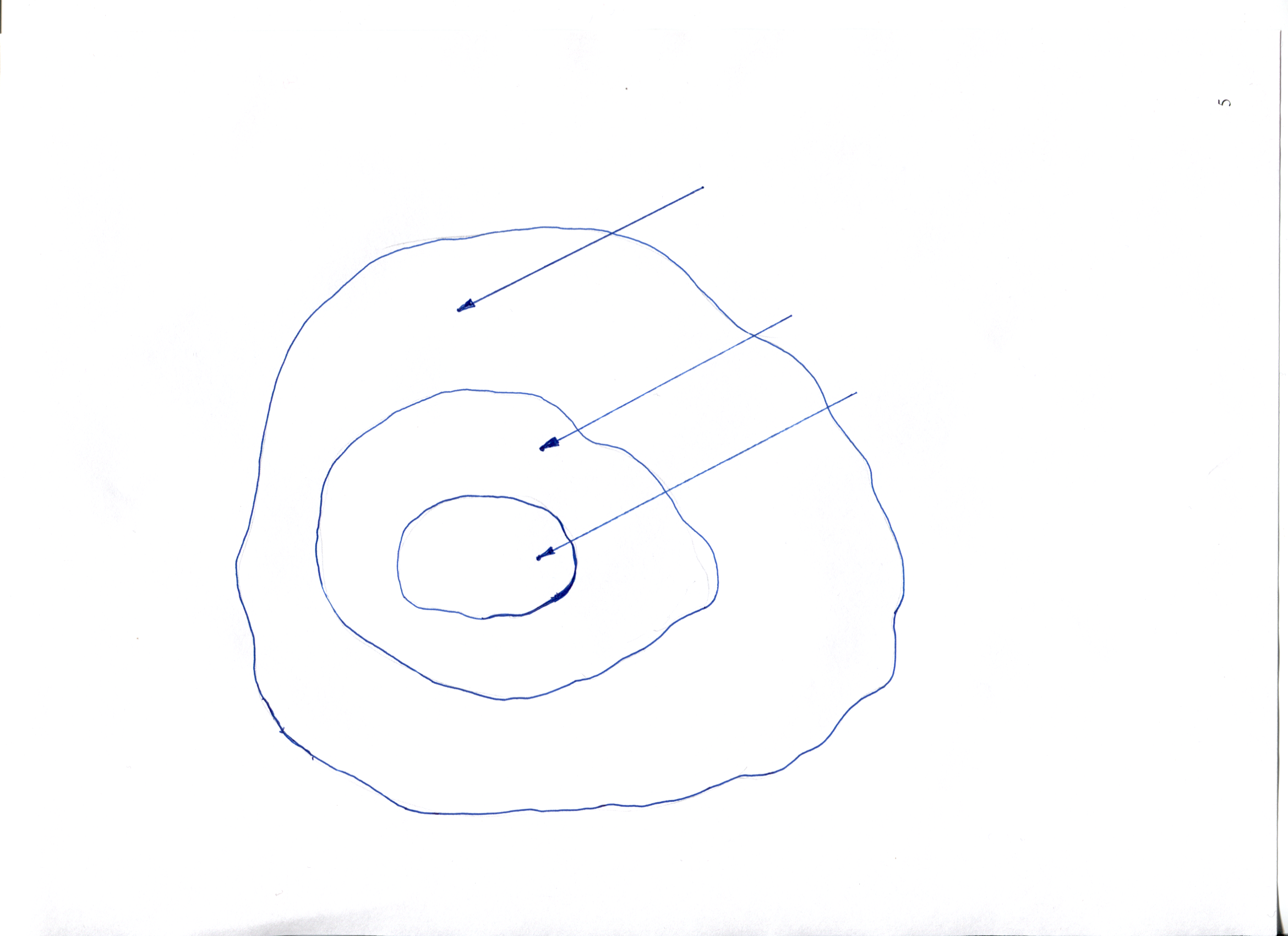наименований) - X .

X Отношения порядка (шкалы порядка) - X .

Отношения аддитивности (шкалы интервалов, шкалы отношений) – X .

( экстенсивные величины )

X

В соответствии с логической структурой свойств в теории измерений принято в основном различать 5 типов шкал измерений: шкалы наименований, порядка, разностей (интервалов), отношений и абсолютные шкалы.

Классическая метрология основное внимание уделяла изучению экстенсивных величин. Эти величины характеризуют вещественные или энергетические свойства объекта (ток, сопротивление, масса тела и т.д.). Для их изучения вводится система физических величин и их единицы (Ампер, Ом, Килограмм и т.д.). Только такие величины могут быть измерены. Как видно из рисунка, экстенсивные величины и объекты, которые они описывают, составляют относительно малую часть из всего множества свойств объектов окружающего нас мира! А как нам использовать мощный аппарат метрологии - основной инструмент познания окружающей нас природы, для изучения других свойств объектов (не измеряемых)?

Таким инструментарием и являются шкалы измерений - принятый по соглашению порядок определения и обозначения всевозможных проявлений (значений) конкретного свойства (величины).

Шкала измерений получается гомоморфным отображением множества элементов такой системы с отношениями на множество чисел или, в более общем случае,- на знаковую систему с аналогичными логическими отношениями. Такими знаковыми системами, например, являются: множество обозначений (названий) цветов, совокупность классификации символов или понятий, множество названий состояний объекта, множество баллов оценки состояний объекта и т. п. При таком отображении используется модель объекта, достаточно адекватно (для решения измерительных задач) описывающая логическую структуру рассматриваемого свойства этого объекта. В соответствии с логической структурой свойств в теории измерений принято в основном различать 5 типов Шкал измерений. Мы их уже называли – это шкалы наименований, порядка, разностей (интервалов), отношений и абсолютные шкалы.

Шкала наименований характеризуется только отношением эквивалентности какого-либо качественного проявления свойства

В шкале наименований (другое название этой шкалы - номинальная; это - переписанное русскими буквами английское название шкалы) допустимыми являются все взаимно-однозначные преобразования. В этой шкале числа используются лишь как метки. Примерно так же, как при сдаче белья в прачечную, т.е. лишь для различения объектов. В шкале наименований измерены, например, номера телефонов, автомашин, паспортов, студенческих билетов. Номера страховых свидетельств государственного пенсионного страхования, медицинского страхования, ИНН (индивидуальный номер налогоплательщика) измерены в шкале наименований. Пол людей тоже измерен в шкале наименований, результат измерения принимает два значения - мужской, женский. Раса, национальность, цвет глаз, волос - номинальные признаки. Номера букв в алфавите - тоже измерения в шкале наименований. Никому в здравом уме не придет в голову складывать или умножать номера телефонов, такие операции не имеют смысла. Сравнивать буквы и говорить, например, что буква П лучше буквы С, также никто не будет. Единственное, для чего годятся измерения в шкале наименований - это различать объекты. Во многих случаях только это от них и требуется. Например, шкафчики в раздевалках для взрослых различают по номерам, т.е. числам, а в детских садах используют рисунки, поскольку дети еще не знают чисел.

Шкала порядка описывает свойства, для которых имеют смысл не только отношение эквивалентности, но и отношение порядка по возрастанию или убыванию количественного проявления свойства. В такого рода шкалах в принципе нет возможности введения единицы измерений, также не имеют смысла суждения, во сколько раз больше или меньше проявления конкретных свойств. Различные варианты шкал порядка для одного и того же свойства связаны между собой монотонными зависимостями. В шкалах порядка может быть (иметь смысл) нуль или его может не быть. Так, шкалы твёрдости начинаются с некоторого ненулевого значения, сейсмическая шкала начинается с одного балла, а шкала Бофорта для силы ветра - с нулевого значения.

В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между объектами. Простейшим примером являются оценки знаний учащихся. Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе ровно тот же смысл выражается словесно - неудовлетворительно, удовлетворительно, хорошо, отлично. Этим подчеркивается "нечисловой" характер оценок знаний учащихся. В порядковой шкале допустимыми являются все строго возрастающие преобразования.

          Установление типа шкалы, т.е. задания группы допустимых преобразований шкалы измерения - дело специалистов соответствующей прикладной области.          Оценки экспертов часто следует считать измеренными в порядковой шкале. Типичным примером являются задачи ранжирования и классификации промышленных объектов, подлежащих экологическому страхованию. Эксперт может сказать (и обосновать), что один показатель качества продукции более важен, чем другой, первый технологический объект более опасен, чем второй, и т.д. Но он не в состоянии  сказать, во сколько раз или на сколько более важен, соответственно, более опасен. Экспертов часто просят дать ранжировку (упорядочение) объектов экспертизы, т.е. расположить их в порядке возрастания (или убывания) интенсивности интересующей организаторов экспертизы характеристики. Ранг - это номер (объекта экспертизы) в упорядоченном ряду значений характеристики у различных объектов. Такой ряд в статистике называется вариационным. Формально ранги выражаются числами 1, 2, 3, ..., но с этими числами нельзя делать привычные арифметические операции. Например, хотя в арифметике 1 + 2 = 3, но нельзя утверждать, что для объекта, стоящем на третьем месте в упорядочении, интенсивность изучаемой характеристики равна сумме интенсивностей объектов с рангами 1 и 2. Так, один из видов экспертного оценивания - оценки учащихся. Вряд ли кто-либо будет утверждать, что знания отличника равны сумме знаний двоечника и троечника (хотя 5 = 2 + 3), хорошист соответствует двум двоечникам (2 + 2 = 4), а между отличником и троечником такая же разница, как между хорошистом и двоечником (5 - 3 = 4 - 2).

Поэтому очевидно, что для анализа подобного рода качественных данных необходима не всем известная арифметика, а другая теория, дающая базу для разработки, изучения и применения конкретных методов расчета. Это - технология измерения (ТИ).

Почему мнения экспертов естественно выражать именно в порядковой шкале? Как показали многочисленные опыты, человек более правильно (и с меньшими затруднениями) отвечает на вопросы качественного, например, сравнительного, характера, чем количественного. Так, ему легче сказать, какая из двух гирь тяжелее, чем указать их примерный вес в граммах. (дегустаторы вин, кофе, ....; эксперты - парфюмеры,,)

В различных областях человеческой деятельности применяется много других видов порядковых шкал. Так, например, в минералогии используется шкала Мооса, по которому минералы классифицируются согласно критерию твердости. А именно: тальк имеет балл 1, гипс - 2, кальций - 3, флюорит - 4, апатит - 5, ортоклаз - 6, кварц - 7, топаз - 8, корунд - 9, алмаз - 10. Минерал с большим номером является более твердым, чем минерал с меньшим номером, при нажатии царапает его.

Порядковыми шкалами в географии являются - бофортова шкала ветров ("штиль", "слабый ветер", "умеренный ветер" и т.д.), шкала силы землетрясений. Очевидно, нельзя утверждать, что землетрясение в 2 балла (лампа качнулась под потолком - такое бывает и в Москве) ровно в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего на поверхности земли).

В медицине порядковыми шкалами являются - шкала стадий гипертонической болезни (по Мясникову), шкала степеней сердечной недостаточности (по Стражеско-Василенко-Лангу), шкала степени выраженности коронарной недостаточности (по Фогельсону), и т.д. Все эти шкалы построены по схеме: заболевание не обнаружено; первая стадия заболевания; вторая стадия; третья стадия… Иногда выделяют стадии 1а, 1б и др. Каждая стадия имеет свойственную только ей медицинскую характеристику. При описании групп инвалидности числа используются в противоположном порядке: самая тяжелая - первая группа инвалидности, затем - вторая, самая легкая - третья.

При оценке качества продукции и услуг, в т.н. квалиметрии (буквальный перевод: измерение качества) популярны порядковые шкалы. А именно, единица продукции оценивается как годная или не годная. При более тщательном анализе используется шкала с тремя градациями: есть значительные дефекты - присутствуют только незначительные дефекты - нет дефектов.

Иногда применяют четыре градации: имеются критические дефекты (делающие невозможным использование) - есть значительные дефекты - присутствуют только незначительные дефекты - нет дефектов. Аналогичный смысл имеет сортность продукции - высший сорт, первый сорт, второй сорт,…

(Недобросовестность статистиков породила и юмористическую шкалу: «Есть ложь обыкновенная, наглая и статистика»).

При оценке экологических воздействий первая, наиболее обобщенная оценка - обычно порядковая, например: природная среда стабильна - природная среда угнетена (деградирует). Аналогично в эколого-медицинской шкале: нет выраженного воздействия на здоровье людей - отмечается отрицательное воздействие на здоровье. Порядковая шкала используется и во многих иных областях. В эконометрике – это, прежде всего, различные методы экспертных оценок.

Все шкалы измерения делят на две группы - шкалы качественных признаков и шкалы количественных признаков.

Порядковая шкала и шкала наименований - основные шкалы качественных признаков. Поэтому измерения в шкалах порядка и наименований иногда называют оцениванием.

         

Шкалы количественных признаков - это шкалы интервалов (разностей), отношений, абсолютная шкала.

По шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой. В этих случаях на шкале нельзя отметить ни естественное начало отсчета, ни естественную  единицу измерения. Исследователь должен сам задать точку отсчета и сам выбрать единицу измерения. Допустимыми преобразованиями в шкале интервалов являются линейные возрастающие преобразования, т.е. линейные функции. Температурные шкалы Цельсия и Фаренгейта связаны именно такой зависимостью: ⁰С = 5/9 ( ⁰F - 32), где ⁰С - температура (в градусах) по шкале Цельсия, а ⁰F - температура по шкале Фаренгейта.

Шкала разностей (интервалов) отличается от шкалы порядка тем, что для описываемого ею свойства имеют смысл не только отношения эквивалентности и порядка, но и пропорциональности или суммирования интервалов (разностей) между различными количественными проявлениями свойства. Характерный пример - шкалы времени; интервалы времени можно суммировать или вычитать, складывать же даты к.-л. событий бессмысленно. Шкалы разностей имеют условный нуль, опирающийся на какой-либо репер (напр., шкала Цельсия, ).

          Из количественных шкал наиболее распространенными в науке и практике являются шкалы отношений. В них есть естественное начало отсчета - нуль, т.е. отсутствие величины. По шкале отношений измерены большинство физических единиц: масса тела, длина, заряд, а также цены в экономике. Допустимыми преобразованиями шкале отношений являются подобные (изменяющие только масштаб). Другими словами, линейные возрастающие преобразования без свободного члена. Шкала отношений описывает свойства, ко множеству количественных проявлений которых применимы отношения эквивалентности, порядка, пропорциональности или суммирования (а следовательно, и вычитания, и умножения). В шкале отношений существует естественный критерий нулевого количественного проявления свойства, т. е. нуль имеет не условное значение, а вполне определенный физический смысл. Примеры шкал отношений - шкала массы, термодинамическая температурная шкала.

Абсолютные шкалы обладают всеми признаками шкал отношений, но дополнительно в них существует естественное однозначное определение единицы измерения. Такие Шкалы измерения соответствуют относительным величинам - отношениям одноимённых физических величин, описываемых шкалами отношений. К таким величинам относятся коэффициент усиления, добротность колебательной системы, коэффициент ослабления и т. п.

Среди абсолютных шкал выделяются ограниченные по диапазону шкалы, значения которых находятся в пределах от 0 до 1. Они характерны для кпд, амплитудной модуляции и т. п. величин. Только для абсолютной шкалы результаты измерений - числа в обычном смысле слова. Примером является число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.

          В процессе развития соответствующей области знания тип шкалы может меняться. Так, сначала температура измерялась по порядковой шкале (холоднее - теплее). Затем - по интервальной (шкалы Цельсия, Фаренгейта, Реомюра). Наконец, после открытия абсолютного нуля температуру можно считать измеренной по шкале отношений (шкала Кельвина). Надо отметить, что среди специалистов иногда имеются разногласия по поводу того, по каким шкалам следует считать измеренными те или иные реальные величины. Другими словами, процесс измерения включает в себя и определение типа шкалы (вместе с обоснованием выбора определенного типа шкалы). Кроме перечисленных основных типов шкал, иногда используют и иные шкалы.

Большинство свойств, которые рассматривают в практической метрологии, описывается одномерными Шкалами измерения. Однако имеются свойства, которые в принципе можно описать только многомерными шкалами. Таковы, например, трёхмерные шкалы цвета в колориметрии. Шкалы сортности изделий и продуктов в общем случае являются многомерными шкалами наименований и опираются на ряд факторов, каждый из которых определяется по специализированным шкалам наименований порядка или по общим шкалам интервалов, отношений и абсолютным, описывающим общепринятые физические величины и параметры (напр., размеры изделия). Практическая реализация шкал конкретных свойств достигается путём стандартизации шкал и единиц измерений, а также способов и условий их однозначного воспроизведения эталонами и средствами измерений. Понятие единицы измерений, неизменной для любых участков шкалы, имеет смысл только для шкал отношений и разностей (интервалов), а также для абсолютных шкал. В соответствии с этим положением единицы измерений, охватываемые международной системой единиц, соответствуют величинам, описываемым только шкалами отношений и разностей. Конкретные математические формулы в науке и технике могут связывать также только такие величины и разности величин, которые описываются соответственно шкалами отношений, разностей и абсолютными.

Для шкал отношений и разностей в некоторых случаях оказывается недостаточным установление только единиц измерений. Так, даже для таких величин, как время, сила света, температуpa, которым в международной системе единиц соответствуют основные единицы - секунда, кандела, кельвин, практическая системы измерений опираются также на специальные Шкалы измерений. Кроме того, сами единицы в ряде случаев определяются с использованием фундаментальных физических констант или метрологических констант (см., напр., Кандела).

По мере развития метрологии наблюдается тенденция рассматривать в качестве объектов измерений все новые, и не только физические, свойства и соответствующие им величины. Так, например, формируется и описан метрологический подход к изучению и описанию свойств биологических., психологических, социальных (в т. ч. экономических) систем, создаются новые и совершенствуются уже существующие Шкалы измерения.

Спорт

Любопытно, но именно в большом спорте достижения законодательно будут подвергаться государственному метрологическому контролю и надзору (раздел 4 закона РФ об обеспечении единства измерений). Естественно это стало возможным благодаря использованию шкал измерений. Давайте рассмотрим особенности метрологического обеспечения спортивных достижений.

Большинство видов спорта можно условно разделить на три группы:

1 группа – в ней превалируют объективные методы оценки результатов измерений;

2 группа – здесь равную роль играют и объективные, и субъективные оценки;

3 группа – здесь используются субъективные оценки.

Кто сможет привести примеры видов спорта, входящих в эти группы?

Пожалуй, самым ярким примером вида спорт первой группы можно назвать тяжелую атлетику.

Атлеты разбиваются по «весовым категориям» (масса тела), а затем результаты фиксируются в килограммах (т.е. измеряется). Это аддитивная шкала измерений (Шкала отношений).

Можно назвать еще целый ряд разделов спорта, для которых могут использоваться шкалы интервалов или отношений. Это прыжковые дисциплины, заплывы в бассейнах и др.

В игровых видах спорта (футбол, хоккей, …) подсчет забитых голов, шайб ведется по абсолютной дискретной (счетной) неограниченной шкале, а окончательный результат определяется в шкале порядка по соотношению засчитанных голов, шайб, очков.

Вторая группа – это спортивная гимнастика, прыжки в воду. Здесь в зачет входят достаточно субъективные коэффициенты трудности (например «рисунок» прыжка), снятие или добавление баллов: влияет «впечатление» судей!

В обоих случаях работают шкалы порядка (с последующим суммированием полученных баллов).

Третья группа – это конечно же фигурное катание, художественная гимнастика, синхронное плавание…

Конечно, и здесь присутствуют количественные оценки, но основную роль играют субъективные впечатления судей и шкалы порядка.

Таким образом, мы видим, что в большом спорте используются все виды шкал (кроме шкал наименований).

Вместе с тем, даже в большом спорте, где результаты имеют большое международное значение, (а в настоящее время и политическое!), Методика Выполнения Измерений (МВИ) – базовый принцип практической метрологии, еще не нашла должного применения.

Еще большая доля неопределенностей имеет место в метрологическом обеспечении общественных, социальных дисциплин (объектов, явлений).

Коснемся области, касающейся каждого жителя страны – образование.

С незапамятных времен, а фактически с появлением образовательных учреждений перед обучающими (любому ремеслу…) вставала задача оценки знаний обучающихся. Так появилась необходимость в балльных шкалах оценок.

Каких только шкал не было!

*двухбалльная – удовлетворительно и неудовлетворительно (кстати, так сегодня оценивается деятельность подразделений вузов: кафедр, лабораторий, да и отчетов преподавателей на Ученом совете).

*четырехбалльная – отлично , хорошо, удовлетворительно, неудовлетворительно (в вузах до введения стобалльных шкал).

* пятибалльная – 5,4,3,2,1 .

* стобалльная – пресловутая ЕГЭ, новая вузовская шкала оценок знаний студентов.

На примере этих шкал особенно хорошо видны особенности шкал порядка. Несомненно, «пятерочник» знает предмет лучше «четверочника» и, особенно, «троечника». А во сколько раз лучше? Вряд ли кто сможет оценить. Не говоря о том, что зачастую «тройка», заработанная в результате самостоятельного, оригинального мышления может быть на самом деле весомее пятерки, заработанной бездумной зубрежкой!

Сегодня много говорится о замене понятий «знания» понятием «компетенция». Ставится важная для современного инновационного периода развития страны задача определения компетенций выпускника вуза, компетенций работника предприятия при оценки его квалификации и т.п. По идее оценка компетенций человека должна ответить на вопрос: в какой мере он способен претворять свои знания в реальный продукт – будь то ремесло, инженерное дело, наука.

(Пример оценки компетентности в России)

Бесконечное многообразие свойств физических объектов затрудняет их отражение совокупностями чисел с ограниченной разрядностью, возникающее при их измерении. Н.Р.Кэмпбелл предложил использовать постулаты математической логики для описания трех наиболее общих проявлений свойств в отношениях эквивалентности, порядка и аддитивности. Это позволило упорядочить классификацию шкал измерений.

1. Отношение эквивалентности--это отношение, в котором данное свойство X у различных объектов А и В оказывается одинаковыми или неодинаковыми.

Постулаты отношения эквивалентности:

а) дихотомии (сходства и различия): либо , либо ;

б) симметричности: если ;

в) транзитивности по качеству: .

* Если свойство проявляет себя только в отношении эквивалентности, то обладающие им объекты могут быть: обнаружены, классифицированы, подвергнуты контролю по классам свойств эквивалентности, отражены соответствующими формальными объектами—числами. Для этого используются шкалы наименований. Эти свойства нельзя считать физическими величинами, поэтому они не являются шкалами ФВ.

Основным информационным параметром совокупности объектов с отношением эквивалентности является их количество, которое определяется путем счета. Например, число зайцев в группе животных данного региона.

2. Отношение порядка—это отношение, в котором данное свойство Х у различных объектов оказывается больше или меньше.

Постулаты отношения порядка:

а) антисимметричности: ;

б) транзитивности по интенсивности свойства: .

*Если свойства, помимо отношения эквивалентности, имеют и количественную ординату (интенсивность), то они отображаются интенсивными величинами.

Интенсивные величины могут быть обнаружены, классифицированы по интенсивности, подвергнуты контролю, количественно оценены монотонно возрастающими или убывающими числами. На основании понятия «интенсивная величина» вводятся понятия физической величины и ее размера. Объекты, характеризующиеся интенсивными величинами, могут быть подвергнуты контролю. Контроль--это процедура установления соответствия между состоянием объекта и нормой. Интенсивные величины оцениваются при помощи шкал порядка и интервалов.

Шкала порядка является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство.

Различают два вида шкал порядка: условные (эмпирические), исходные значения которой выражены в условных единицах (Пример: 12-бальная шкала Ботфорта для силы морского ветра, шкала вязкости Энглера); шкалы порядка с нанесенными на них реперными точками

( Пример: шкала Мооса для определения твердости минералов содержит 10 опорных (реперных) минералов с различными условными числами твердости:

Тальк-1, чипс-2, кальций-3, флюфит-4, апатит-5, ортоклаз-6, кварц-7, топаз-8, корунд-9, алмаз-10.

Минералу присваивается твердость (число) на основании эксперимента: испытуемый материал царапается опорным. Если от кварца (7) – след, а от ортоклаза (6) – нет следа, то твердость испытуемого минерала лежит в интервале 6  Х  7 ). Такой эксперимент называется контролем.

Контроль – это процедура установления соответствия между реальным состоянием объекта и нормой.

Результат контроля определяется следующим уравнением:

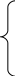
ниже нормы (Х Х_н);

= норма (Х_н< ХХ_в); (2.1)

выше нормы (ХХ_в), где

Х_н – нижняя граница нормы

Х_в – верхняя граница нормы.

Таким образом, определение значения величин при помощи шкал порядка нельзя считать измерением, т.к. на этих шкалах не могут быть введены единицы измерения.

Операцию по приписыванию числа требуемой величине называют оцениванием. Такие величины называют оцениваемые ФВ. Сам эксперимент называется контролем.

Оценивание по шкале порядка является неоднозначным и достаточно условным.

3. Отношение аддитивности—это отношение, когда однородные свойства различных объектов могут суммироваться.

Постулаты отношения аддитивности:

а) монотонности: ;

б) коммутативности: ;

в) дистрибутивности: ;

г) ассоциативности: .

*Если ФВ проявляется в отношениях эквивалентности, порядка и аддитивности, то она может быть: обнаружена, классифицирована, проконтролирована и измерена. Эти величины называются экстенсивными ; экстенсивные величины характеризуют вещественные или энергетические свойства объекта (ток, сопротивление, масса тела…). Для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности, применяют шкалы интервалов, шкалы отношений и абсолютные шкалы.

Шкала интервалов величины описывается уравнением:

= _о + q [ ] , где (2.2)

q-числовое значение ФВ; _о – начало отсчета шкалы; [ ] - единица ФВ

Задается шкала с помощью реперных точек: _о и ₁, которые можно реализовать (воспроизвести) физически.

Пример: в 1715 г. американский ученый Фаренгейт изобрел ртутный термометр. В качестве реперных точек он взял значения:

_о - температура смеси льда, поваренной соли и нашатыря (экспериментально получаемая).

₁ – температура человеческого тела.

Он разделил интервал ₁ – _о на 96 равных частей (видимо исходя из основания «12», в результате это приводит к сложностям при переходе к градусу Цельсия).

В результате была получена единица измерения – градус Фаренгейта (до сих пор применяется в США):

[ _F] =

Т емпература таяния смеси льда, соли и нашатыря оказалась равной 32^оF; а температура кипения воды : 212^оF

Рис. 2.3 Температурная шкала Фаренгейта

В качестве второй реперной точки была взята температура кипения воды (при нормальном давлении это более стабильная и точная величина, чем температура тела человека).

В 1742 г. шведский ученый А.Цельсий ввел свою шкалу на ртутном термометре с реперными точками: ₀ – температура таяния льда (тройная точка воды)

₁ – температура кипения воды при нормальном давлении.

[ _c] =

Рис. 2.4 Температурная шкала Цельсия

Эта шкала (метрическая) оказалась более удобной, однако американцы до сих пор пользуются шкалой Фаренгейта (национальный престиж).

Имея разные шкалы одинаковых ФВ экспериментатор должен уметь переводить показания одной шкалы в другую.

Перевод осуществляется следующим образом:

= _о1 + q₁[ ]₁ – одна шкала

= _о2 + q₂[ ]₂ – другая шкала

Тогда: q₁= (2.3)

Пример:

Требуется перевести температуру по Фаренгейту в температуру Цельсия.

Значение разности температур между точкой кипения воды и точкой таяния льда составляет:

212^оF – 32^оF = 180^оF – по шкале Фаренгейта

100^оС – О^оС = 100^оС – по шкале Цельсия

Таким образом,

180^оF = 100^оС

и следовательно:

В результате, используя (2.3), получим:

Т_с=

Пусть Т_F = 80^оF, тогда Т_c = 26,7^оС

Шкала отношений – самая совершенная шкала. В этих шкалах существует однозначный

естественный критерий нулевого количественного проявления свойства и единица измерения, установленная по соглашению, т.е. это шкалы интервалов с естественным началом отсчета.

Эти шкалы описываются уравнением = q[ ] (2.4)

Переход от одной шкалы к другой реализуется просто: q₂ =

Пример: В середине XIX века лорд Томсон (Кельвин) и одновременно Д.И.Менделеев предложили построить термодинамическую шкалу по одной (естественной) реперной точке, в качестве которой взята точка абсолютного нуля; О^оК (О^оК = - 273,16^оС)

- Кельвин – единица термодинамической температуры,

где 273,16К – тройная точка воды

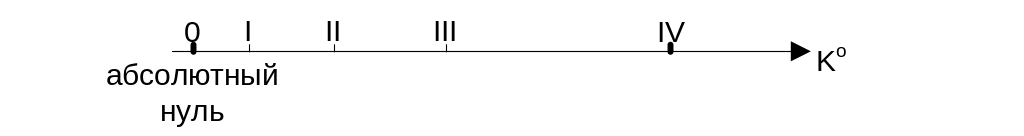
I: 13,81К – тройная точка водорода

II: 54,361К – тройная точка кислорода

III: 90,188К – точка кипения кислорода

IV: 273,16К – тройная точка воды

Операция по получению экстенсивной величины называют измерением. Такие величины являются измеряемыми ФВ. В результате эксперимента (измерения) получаем значение ФВ.

Методика выполнения измерений.