4. Метод координат
Пример 15. Найдите площадь четырехугольника, вершины которого имеют координаты (2;3), (2;7), (9;0), (9;4).
Решение. Данный четырехугольник является параллелограммом. В качестве основания параллелограмма возьмем сторону параллельную оси ординат. Ее длина равна 4. Тогда длина высоты, опущенной на основание, равна 7. Площадь параллелограмма равна 74 = 28.
Ответ: 28.
Пример 16.
Найдите площадь треугольника, вершины которого имеют координаты А(2;3), В(6;9), С(8;2).
Решение.
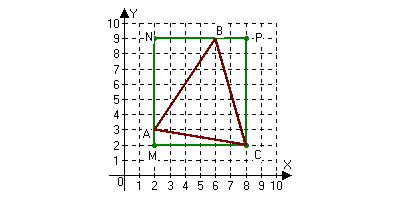
Рассмотрим прямоугольник с вершинами М(2;2), N(2;9), P(8;9) и C(8;2). Его площадь равна произведению длин сторон MN и MC: 67 = 42. Вычислим площади треугольников ANB, BPC и MAC: SANB = ½ ANNB = 12, SBPC = ½ BPBC = 7, SMAC = ½ MAMC = 3. Вычтем из площади прямоугольника MNPC площади треугольников ANB, BPC и MAC и, тем самым найдем площадь треугольника АВС: 42 – 12 – 7 – 3 = 20.
Ответ: 20.
Тренировочные задания
1) [2] В треугольнике длины сторон рвны 3, 5, n, где n – натуральное число. Укажите возможные значения n.
( Отв. 3, 4, 5, 6, 7).
2) [2] В равнобедренной трапеции диагональ
составляет с боковой стороной угол
.
Боковая сторона равна меньшему основанию.
Найти острый угол трапеции.
( Отв.
).
3) [2] Около окружности описана равнобедренная трапеция с боковой стороной, равной 10. найти среднюю линию трапеции.
(Отв.
).
4) [2] Найти высоту прямоугольного треугольника, опущенную на гипотенузу, если эта высота делит гипотенузу на отрезки, равные 3 и 12.
( Отв.
).
5) [2] Найти гипотенузу прямоугольного треугольника, если радиус описанной около этого треугольника окружности равен 4.
(Отв.
).
6) Отношение периметров двух ромбов с равными острыми углами равно 3. Найдите отношение площадей этих ромбов.
(Отв. 9).
7) Найти площадь ромба, если длина одной из его диагоналей равна 12, а длина другой на 25% больше.
(Отв. 90 ).
8) Найти длину дуги в
,
если радиус окружности равен 3.
(Отв.
).
9) [2] Найти радиус описанной около
треугольника окружности, если его
сторона, равная 4,
лежит против угла в
.
( Отв.
).
10) [2] В параллелограмме угол между
высотами, проведенными из вершины тупого
угла, равен
.
Найти тупой угол параллелограмма.
( Отв.
).
11) Вписанный треугольник разбивает окружность на дуги, длины которых равны 120, 280 и 320. Найдите наибольший угол треугольника.
(Отв.
).
12) [2] Биссектриса угла А параллелограмма ABCD делит сторону BC на отрезки BK = 49 и
KC = 81. Найти периметр параллелограмма.
( Отв.
).
13) [4] Один из углов равнобедренного
треугольника равен
.
Найдите другие углы треугольника.
( Отв.
).
14) [4] Один из углов равнобедренного
треугольника на
больше другого. Найдите меньший угол
треугольника.
( Отв. ).
15) [4] В треугольнике ABC
AD
– биссектриса, угол C
равен
,
угол CAD
равен
.
Найдите угол B.
( Отв.
).
16) [4] Найдите острый угол между биссектрисами острых углов прямоугольного треугольника.
(Отв.
).
17) [4] В треугольнике ABC
угол A
равен
,
угол В
равен
.
AD,
BE
и СF
– биссектрисы, пересекающиеся в
точке О.
Найдите угол AОF.
( Отв.
).
18) [4] В прямоугольнике диагональ делит
угол в отношении
.
Меньшая сторона прямоугольника равна
6. Найти диагональ
данного прямоугольника.
( Отв.
).
19) [4] Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
( Отв.
).
20) [4] Найдите площадь четырехугольника,
вершины которого имеют координаты
.
( Отв.
).
Стереометрия
Призмы
Введем следующие обозначения:
l – боковое ребро призмы, P – периметр основания, S – площадь основания, H – высота,
Pсеч – периметр перпендикулярного сечения, Sбок – площадь боковой поверхности,
V – объем.
Основные формулы:
Sбок = Pсеч l; V = SH;
Прямая призма:
Sбок = Pl;
В прямоугольном параллелепипеде a, b, c – длина, ширина и высота параллелепипеда, d – его диагональ. Тогда
V = abc; d2 = a2 + b2 + c2
В кубе с ребром равным a: V = a3; d = a .
Пример 1. Диагональ куба равна 2
.
Найдите площадь его поверхности.
Решение. Поскольку диагональ куба d = a , составим уравнение: a = 2 . Решая его, получим a = 2. Площадь грани куба равна a2 = 4, всего у куба 6 граней, следовательно, площадь его полной поверхности равна 24.
Ответ: 24.
Пример 2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. При этом уровень воды достиг 16 см. Затем эту воду перелили в сосуд, имеющий форму куба, и оказалось, что он полностью заполнен водой. Найдите сторону основания треугольной призмы, если известно, что ребро куба равно 2 .
Решение. Обозначим сторону основания
треугольной призмы буквой а, тогда
площадь основания призмы
(см.
список формул по планиметрии). Объем
воды в треугольной призме равен 16S
=
и равен объему куба. Объем куба с ребром
2
равен 24 . Составим уравнение: = 24 . Решая его, получим, что а = .
Ответ: .