4.1.6. Апріорна інформація

Апріорною інформацією називають інформацію, яку не­обхідно зібрати, опрацювати і ввести в ЕОМ, щоб можна було розв'язати задачу аналізу ТС при допустимих машинних ресурсах або зменшити вимоги до них. Розглянемо визначення апріорної інформації на конкретних прикладах.

Приклад 4.3. Розв'язування системи кінцевих рівнянь. У ба­гатьох випадках обчислення, які пов'язані з аналізом ТС на ЕОМ, вимагають розв'язування системи кінцевих (алгебраїчних або транс­цендентних) рівнянь:

(4.4)

{/і(х_ьх_ь...,х₁)=0, або у векторній формі

/(Х) = 0. (4.5)

Деякі обчислювальні алгоритми дають змогу розрахувати корінь

137

о--

лише тоді, коли в машину введено певне достатньо близьке до у значення вектора Хо.

Інші алгоритми приводять до розв'язку системи (4.4) або (4 ^\ • тоді, коли про Хо нічого не відомо, однак значення Х0 дає змо суттєво прискорити розрахунок кореня. Зрозуміло, що визначенн Хо природно інтерпретувати як знаходження апріорної інформації

А

Інколи передбачувані значення Хц практично невідомі, тоді необхідно говорити про цілу, достатньо протяжну область О V

просторі координат Х\^,х₂^, >^ХЮ> У ^якій повинна знаходитися

необхідна для розв'язку системи (4.4) точка. В такій ситуації апріорною інформацією є, очевидно, опис області С_х.

Приклад 4.4. Розрахунок періодичних режимів руху ТС. Аналіз ряду ТС пов'язаний із властивістю періодичності їх руху. Ця вла­стивість інколи визначає робочий режим функціонування системи (періодичні коливання механічних систем і машин), а інколи пов'язана з порушенням робочого режиму. Дослідження властивості періодичності зводиться до знаходження умов, при яких існують або завідомо відсутні періодичні розв'язки деяких рівнянь, що входять в опис системи. Найчастіше необхідно знайти і самі розв'язки, хоча б наближено.

Нехай опис системи зведено до системи звичайних дифе­ренціальних рівнянь у так званій нормальній формі Коші:

.., х₁,и_ь и₂,..., и_т);

,(4.6)

= <Рі(і,х_ь х₂,..., х_ьи_ьи₂,..., и_т)

або у векторній формі

де / - час; ІДУ) = {Ні,«2'--->^и_т} ' ^ве^кт°Р вхідних Д#; Х(і)= —{хі, х₂, •..,*/} - вектор стану системи, який необхідно

знайти в результаті розв'язування системи (4.6) або (4.7).

Для багатьох технічних систем з періодичності функцій ), ...,Х[(і) випливає періодичність відгуків системи

138

(і),..., Уп^)- У таких випадках задача зводиться, по суті, до зна-одокення періодичних розв'яків для Х(ї). Тепер вияснимо, яку роль тут відігр^ає апріорна інформація.

Добре відомо, що розв'язок Х(ґ) для системи (4.6) ви­значається початковими умовами Х(0), тобто сукупністю (Хі(0)>'-ч-^х;/(0)Ь Може статися так, що в просторі координат хА0),--->^хіФ) існує область С_х, яка відрізняється такою вла­стивістю: якщо Х(0) належить С_х, то розв'язок виявляється періодичним, у протилежному випадку розв'язок Х(ї) завжди непе­ріодичний. У більшості технічних систем область С_х не збігається з усім простором, а обмежена. Більше того, область О _х може бути досить складною й заплутаною. Якщо розраховувати періодичні розв'язки і, як наслідок цього, періодичні режими руху технічної системи для певних початкових умов, то знання області С_х цілком необхідне. В іншому випадку область О_х довелось би шукати в рамках деякої процедури, що, звичайно, вимагало б допоміжних машинних ресурсів. Таким чином, розрахунок області С _х є знаход­женням необхідної апріорної інформації.

В обох розглянутих нами прикладах метою збирання й оброб­ки апріорної інформації є визначення області О_х у якомусь про­сторі. Відносно області С нас можуть цікавити два питання: 1) чи дійсно всі точки цієї області мають необхідні нам властивості (наприклад, чи з усіх її точок починаються траєкторії, що приводять до періодичних рухів); 2) наскільки тісно область О облягає ту об­ласть, яка тільки і має розглянуту властивість.

Розглянемо три випадки, які показано на рис 4.2. Для про­стоти ми обмежимось областями на площині, тобто вважаємо, що вектори X двомірні.

На рис. 4.2 кружечками відмічено ті точки області О, які да­ють періодичні режими руху технічній системі.

139

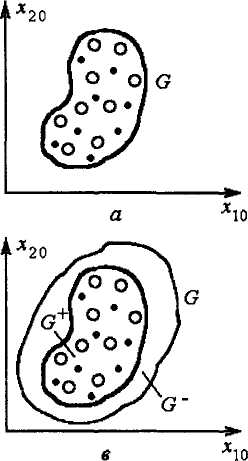
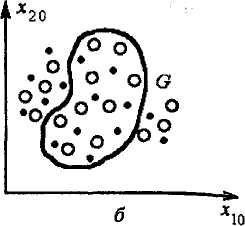
Рис. 4.2. Область О початкових умов, що забезпечують існування заданих властивостей (періодичнихре­жимів руху) технічної системи

Ситуація, що показана на рис. 4.2, а, відповідає ідеальному ви­падку: область С складається тільки з точок, які з максимальною точністю і повнотою описують апріорну інформацію. На рис. 4.2, б область О складається з точок, які не повністю описують апріорну інформацію, бо за межами області О є точки, які задовольняють початкові умови для циклічних режимів руху технічної системи. Об­ласть С повинна була б бути більш повною, ніж на рис. 4.2, б. Однак нам це невідомо, і, можливо, повна межа області визначиться лише після розрахунків на ЕОМ. Третій можливий випадок показано на рис 4.2, в. Тут область С охоплює не тільки бажані точки (вони утворюють область С ⁺), але і зайві (область С~). Очевидно , почавши розрахунки з точок, котрі належать області С~~, ми не отримаємо бажаного результату. В цьому випадку наша апріорна інформація неточна.

З розглянутого прикладу можна зробити висновок, ш° існують два небажаних випадки опису апріорної інформації на стадії попереднього дослідження системи: неповнота (рис. 4.2, 6) і не­точність (рис. 4.2, в). Кількісна оцінка цих факторів можлива лише ймовірнісними методами. Наприклад, можна оцінити ймовірність ситуації, яка подібна тій, що показана на рис. 4.2, б, або оцінит^й

140

статистичні характеристики випадкових величин, що характеризу­ють область С-.

Жорсткі рекомендацій до вибору апріорної інформації в тому чи іншому вигляді (рис. 4.2) дати практично неможливо. Для випад­ку, показаному на рис. 4.2, а, необхідні значні витрати ресурсів на підготовку апріорної інформації, але при цьому значно зменшують­ся витрати на обчислювальні операції. У випадках (рис.4.2, 6, в), на­впаки, зменшуються витрати на підготовку апріорної інформації, зате збільшуються витрати на обчислювальні операції. При цьому співвідношення між одними і другими витратами значною мірою за­лежать від точності визначення області С, яка може бути звуженою або розширеною.

4.1.7. Приклад машинного аналізу технічної системи

Розглянемо структуру процесу машинного аналізу на прикладі розрахунку періодичних коливань технічної системи. Припустимо, що розв'язок системи (4.7) при вибраних нами початкових умовах належить області С_х і є неперіодичним. У процесі діалогу з ЕОМ дослідник у завчасно визначених ним точках осі і буде отримувати інформацію про розв'язок Х(і) та його періодичність. При наявності цієї інформації неперіодичність процесу руху механічної системи можлива в двох випадках: 1) розв'язок в дійсності неперіодичний; 2) розв'язок періодичний, але розрахунок перехідного процесу ще не закінчено. Вияснити причину неперіодичності процесу дослідник може декількома шляхами.

1. Спинити процес обчислень через деякий час і тим самим вне­сти певний вклад у задачу аналізу — визначити властивості системи. Прийняттю такого рішення може сприяти апріорна інформація іншого характеру, ніж та, яку пов'язували з областю С_х. Такою інформацією може бути час установлення періодичного режиму ру­ху механічної системи (д. Якщо за апріорними даними час установ­лення періодичності руху повинен бути певної величини, а розра­хунковий відрізок процесу складає до моменту прийняття рішення значно більшу величину часу, то рішення про спинення обчислювального процесу є виправданим. Однак при цьому задача

141

аналізу з розрахунку періодичності руху механічної системи зал шається невиконаною.

2. Продовжувати процес обчислень, щоб з'ясувати, чи встан виться в подальшому періодичний режим руху. При цьому тако можна використати допоміжну апріорну інформацію.

3. Частково спинити процес обчислень і перевірити достатність описової й апріорної інформації. Може бути, що апріор_Нот інформації достатньо, а описової — недостатньо або навпаки. Може статися так, що необхідно уточнити апріорну інформацію, наприк­ лад, величину ід. Ця величина може виявитися випадковою. М_и вважаємо, що технічна система і зовнішні дії на неї детерміновані тому й ід повинно бути детермінованим числом. Однак, якщо сис­ тема складна та інформація про ід апріорна, то визначити величину ід з достатньою точністю неможливо. Використовуючи будь-який метод оцінки, вдається визначити лише діапазон, у якому з певною ймовірністю повинна знаходитися величина ід.

4.2. Синтез технічних систем 4.2.1. Суть задачі синтезу технічної системи

Постановка задачі синтезу певною мірою зворотна постановці задачі аналізу. В процесі синтезу задаються описи вхідних дій і опи­си поведінки, характеристики й властивості майбутньої системи. До­сить часто в описи поведінки системи входять описи виходів. Ці описи або їх частина в аналізі не задавались, а шукалися. В задачі синтезу необхідно знайти опис самої системи та її стани, в той час як у задачі аналізу опис системи заданий. Таким чином, розв'язування задачі синтезу являє собою процес перетворення одних описів в інші. Ця задача аналогічна задачі аналізу, тільки вхідні і вихідні описи тут інші й сам процес перетворень описів також інший. Саме ці принци-пові різниці роблять процес синтезу більш творчим, де головну роль відіграє кваліфікований спеціаліст, якого не може замінити ніяка су­купність обчислювальних засобів. Однак нерозумно завантажувати спеціаліста громіздкою одноманітною інформацією, яка не вимагає творчих здібностей та інтуїції. Тому в процесі синтезу технічних систем бажано організувати взаємодію людини й ЕОМ.

У процесі синтезу технічних систем центральне місце займають проблеми вибору структури системи і базисних елементів. Ці

142

бл в багатьох задачах дуже погано формалізуються та алго­ритмізуються. Саме тут повинна проявлятися творча сила людсько­го інтелекту, його вміння користуватися інтуїцією, досвідом розв'язування подібних або суттєво інших задач і т. д.

Одним із шляхів синтезу технічних систем є вибір певної струк­тури й базисних елементів і на основі розв'язування задачі аналізу здійснення зондування параметрів системи та вибір таких з них, які задовольняють бажані властивості системи. Якщо аналіз направле-ллй, то його можна будувати таким чином, щоб наблизитися до ба­жаних властивостей системи. Так чи інакше нам удається встанови­ти залежність між характеристиками властивостей системи і пара­метрами її базисних елементів.

На перший погляд здається, що такий підхід досить простий. Однак в дійсності нам не зовсім зрозуміло, яку саме систему не­обхідно аналізувати. Система тільки створюється, і її опис нам не­обхідно знайти, тоді як для задачі аналізу він повинен бути відомим. Так ми стикаємося з основним протиріччям задачі синтезу, яке принципово усунути неможливо. Створення системи вимагає інформації про її поведінку, характеристики та властивості, а саму систему ще треба відшукати. Раніше, ніж опис системи буде знайде­но, цю інформацію неможливо отримати, а не знаючи її, неможливо створити систему.

Основне протиріччя процесу синтезу пов'язане й з іншими, та­кож достатньо суттєвими причинами. їх можна охарактеризувати таким чином: створити систему вдається лише тоді, коли ми знаємо, яку систему ми хочемо створити. Однак це знання приходить лише в процесі знаходження необхідної нам системи і, по суті, багато пи­тань залишаються неясними і після того, як опис системи знайдено, а сама вона реалізована. Бувають випадки, коли постановка задачі синтезу виявляється лише після досить довгої екплуатації системи, тобто коли сама проблема синтезу, можливо, вже не викликає інтересу. Для підтвердження цієї думки розглянемо приклад.

Приклад 4.5. Нехай створюється деяка механічна система, для якої основним робочим режимом є коливальний процес. Діапазон частот цього процесу відомий ще до початку проектування, інші початкові дані також не викликають сумніву. Після того, як задача синтезу була розв'язана і було знайдено опис механічної системи, здійснили її дослідження. В результаті було встановлено, що поряд із коливаннями в заданому частотному діапазоні система здійснює паразитні" коливання, спектр яких знаходиться поза цим

к 143

діапазоном і які недопустимі з точки зору нормальної експлуатя - системи (можуть зруйнувати систему, впливають на її взаємодц^ іншими системами тощо). ³

У результаті розгляду цього прикладу виникає питання-розв'язали ми задачу синтезу чи не розв'язали. Якщо під розв'язко проблеми синтезу розуміти знаходження будь-якої системи, що _За довольняє початкові вимоги, то ми, звичайно, розв'язали зада^ Але якщо мета проектування становить знаходження опису _Ме^ ханічної системи, що задовольняє її ефективне функціонування, то проблема залишилась нерозв'язаною. Протиріччя полягає в тому що виконати формально описані умови ще не означає задовольнити "істинні" умови синтезу.

З розглянутого прикладу видно, що вимогу відсутності пара­зитних коливань необхідно було включити в постановку задачі син­тезу. Однак важливість цієї умови стала очевидною лише після про­ведення аналізу створеної механічної системи. До цього інженер, який формулював задачу, не підозрював про можливість виникнен­ня небажаних процесів. Необхідно зауважити, що при невдалому проведенні аналізу він міг не зафіксувати небажані ефекти і на на­ступній стадії розробки системи.

Досвід створення складних технічних систем показує, що на початку процесу синтезу неможливо формалізувати всі умови, щоб вважати систему задовільною або, тим більше, найкращою з можли­вих. Визначеність у заданні вимог приходить лише з розумінням по­ведінки, характеристик і властивостей системи — тієї самої системи, опис якої невідомий та який необхідно знайти. Звичайно, ці про­тиріччя майже не проявляються у випадку нескладних систем, по­ведінка, характеристики й властивості яких по суті легко пере­дбачувані, хоча б якісно.

Зрозуміло, якщо процес синтезу завершено, то описане вище протиріччя повинно бути рано чи пізно усунутим. Знімається воно одноразовим або багаторазовим звертанням до процесу аналізу та оцінкою його результатів. Таким чином, аналіз виступає основним засобом для зняття протиріччя, що виникає в процесі синтезу технічних систем.

Принципові труднощі процесу синтезу — незнання того, ш° можливе і що неможливе в створюваній системі, і невміння фор­малізувати побажання проектувальника — можуть бути зняті, якщо проаналізувати деякий варіант системи. Виходячи з цього, можна запропонувати таку структуру процесу:

144

1. Розоробити варіант опису технічної системи, який задоволь- _е початкові вимоги синтезу.

2. Провести ґрунтовний аналіз запропонованої системи. На цьому етапі розробити варіант опису технічної системи, який задо­ вольняє початкові вимоги синтезу.

3. Провести ґрунтовний аналіз запропонованої системи. На цьому етапі бажано використати ЕОМ.

4. Оцінити переваги запропонованої системи на основі отри­ маної інформації про її поведінку, характеристики і властивості.

Якщо система задовольняє необхідні вимоги або, тим більше, є найкращою із усіх можливих, то процес синтезу необхідно закінчити, а якщо — ні, то повернутися до першого пункту. Така структура синтезу дає змогу людині й ЕОМ робити те, що у кожного з них виходить найкраще. Пропонування ідей, формування гіпотез, оцінка — все, що вимагає неформального, творчого підходу, зали­шається за людиною. Все, що краще алгоритмізується, в основному виконується ЕОМ. Але справа не тільки в цьому. Кожний вдалий крок в описаній вище ітеративній, циклічній процедурі дає мож­ливість що-небудь нове зрозуміти в системі, яка створюється: посту­пово визначаються межі можливого і неможливого, виявляються не­дооцінені або непомічені небезпечності, формалізуються цілі синтезу й ін. Таким чином, крок за кроком усуваються перешкоди, знімаються протиріччя.

Описана структура процесу синтезу є лише основою складно­го, розгалуженого процесу. Наприклад, задання опису системи ви­магає задання структури, базису елементів і параметрів. Чи дає ви­явлення всіх цих компонентів можливість запропонувати варіант опису системи ? Здебільшого — ні. В усякому разі, визначення па­раметрів системи людина виконує гірше, ніж на ЕОМ. Розрахунок параметрів часто вдається представити у вигляді стрункого алго­ритму, який допускає ефективне використання ЕОМ. Тоді за люди­ною залишається творча робота, а отримані під час цієї роботи ре­зультати опису системи доповнюються чисельною інформацією від ЕОМ.

Звернемось до прикладу 4.2, який описано вище. Задання опи-^СУ колони доцільно звести до вибору самої структури (рис. 4.1) і визначення базису елементів, тобто набору форм поперечних пе-

РерІЗІВ КОЖНОГО 3 елементів. Що СТОСУЄТЬСЯ ВИЗНаЧеННЯ ЧИСеЛ 5}, ТО

Цей розрахунок швидше і точніше виконає ЕОМ. До того ж, подібні Розрахунки можна підпорядкувати різним вимогам, наприклад по-

145

старатися підібрати 5_г- таким чином, щоб колона мала (при задат, структурі і базисі) мінімальну вагу. Іншим важливим моментом розглянутій процедурі синтезу є оцінка доцільності знайденого технічного рішення на третьому етапі. Якщо задача синтезу колони поставлена таким чином, щоб її вага не була більшою за певну _Ве. личину, то в результаті оцінки ваги отриманої конструкції прид. мається певне рішення. Якщо поставлена умова виконується, _То процес синтезу закінчується, а якщо ні, то продовжується до отри­мання бажаного результату. У випадку, коли дані, отримані на дру. гому етапі, не можна поліпшити, то необхідно поступитися деяким старим побажанням, наприклад, погодитися на збільшення ваги ко­лони. Так або інакше, оцінку придатності знайденого варіанта сис­теми необхідно зробити гнучкою, щоб вона добре адаптувалась до отриманих у процесі синтезу нових даних.

Розглянемо варіант, коли необхідно повертатися до першого етапу із заміною нового варіанта структури системи та її базису. Тут необхідно враховувати, що всі накопичені в процесі синтезу знання — виконання процедури аналізу (етап 2), оцінка отриманого рішення (етап 3), — все це впливає на формування ідеї про нову структуру або про новий базис елементів. Переглянувши декілька варіантів, наприклад, поперечних перерізів елементів колони (рис. 4.1), з'ясувавши, які з поставлених умов були виконані, а які ні, зро­зумівши, якою він хоче бачити систему, конструктор пропонує такі нові описи системи, що після розрахунку їх параметрів можна прий­ти до висновку або про її прийнятність (кращого варіанта йому не знайти), або неможливість розв'язати задачу синтезу системи.

4.2.2. Про зміну постановки задачі синтезу

Як було показано раніше, синтез нерозривно пов'язаний із ро­зумінням того, як веде або повинна вести себе система, які її власти­вості, характеристики, параметри і т. д. Приріст відповідної інформації не може не змінити постановки задачі синтезу. Якщо розглянути приклад 4.5 із паразитними коливаннями механічної системи, то можна говорити про дефект початкової постановки: во­на не врахувала важливої вимоги, яка б забороняла системі прояв­ляти коливальні властивості поза робочим діапазоном частот. Після того, як цей недолік системи був проаналізований конструктором' він, природно, ввів таку заборону, і постановка задачі змінилась.

Однак постановка задачі може змінюватися більш суттєво.

146

Покажемо це на прикладі (приклад 4.6) циклічної зміни будь- якої характеристики технічної системи, яка становить функцію V (і) єдиного аргументу і (рис. 4.3). В ідеалі характеристика у(/) повинна . являти собою

^ ^ ^х прямокутник з

висотою Уд, по­ будований на ос­ нові ?о> і і (функ­ ція 1). Певно така характеристика взагалі не може бути реалізована або вона фізично допустима, але її *о ^Г2 ^гі реалізація вима-

_..,.,, . . гає значних вит-

Рис. 4.3. Можливі варіанти характеристики коштів Тому

системи, що синтезується: 1 - ідеальна; ' *

~ -, на початку синте-

2- з піковим виступом; 3 -зплавною конструктор

зміною параметра у '

^{ґ г} системи вказує,

що він згоден на відхилення від функції 1, але вимагає, щоб це відхи­лення — певним чином виміряне — не перевищувало вказаного ним граничного значення. Виберемо за міру відхилення кривої 2 від функції, зображеної прямокутником 1, заштриховану площу і по­значимо її (5 21- Тепер можна сформулювати вимоги до системи, яку

треба синтезувати. Варіант системи задовольняє встановлені вимоги тоді і тільки тоді, коли

8₂₁<д₀, . (4.8)

де 5 о - граничне значення відхилення.

Необхідно побудувати алгоритм синтезу таким чином, щоб він Досягав зменшення заштрихованої площі до тих пір, поки нерівність (4.8) не стане виконаною. Як тільки це станеться, й інші вимоги до системи також будуть виконані, процедуру синтезу можна вважати завершеною. Тоді будь-яка система, що задовольняє вказані вимо­ги, відповідно до початкової постановки задачі вважається за­довільною. В багатьох випадках знання величини #21 ^та виконання

Умови (4.8) для конструктора, який приймає рішення про закінчення Процесу синтезу, є недостатнім. Він бажає ще побачити характери-

147

стику V (/) у вигляді графіка 2 на рис. 4.3. Розглядаючи криву 2 робник системи може, наприклад, прийти до висновку про недот, тимість інтенсивності появи виступу, який має місце при і = і >, цьому випадку він може відхилити отриманий опис системи, хоча к нерівність (4.8) і була при цьому виконана.

Для отримання кращого рішення системи розробник починає процедуру синтезу спочатку, але при цьому вводить допоміжт, інформацію в початкову постановку задачі. Нехай при новому про-цесі синтезу отримано характеристику 3 (рис. 4.3), а величина 5,.

перевищила раніше визначену межу Зо, тобто нерівність (4.8) не ви­конується. Проаналізувавши ситуацію, розробник системи може прийти до висновку, що отримане рішення системи є прийнятним. Відсутність небезпечних виступів може виявитися настільки важли­вою перевагою нової характеристики, що розробник згоден і на по­рушення висунутої спочатку умови (4.8), і на сильне відхилення кри­вої 3 від прямокутника при 1 = 1\. Однак можлива й така стратегія пошуку, при якій розробник системи намагається зменшити ^і і

разом з ним ліквідує небезпечні виступи характеристики 2.

На основі розглянутого прикладу 4.6 приходимо до таких важливих висновків: 1) початково сформульована (до розв'язування задачі) постановка проблеми синтезу може не включати важливих вимог, які стають пізніше досить очевидними; 2) зміни постановки задачі майже неминучі в ході синтезу складних технічних систем; 3) у багатьох випадках оцінку переваг системи, знайденого проектного рішення неможливо або недоцільно формалізувати, тобто зводити до перевірки чисто кількісних вимог.

Найбільш показовим моментом виявляється тут невідтворюваність оцінки результатів. Інший розробник сис­теми при подібному підході може віддати перевагу іншій ха­рактеристиці у(і). Більше того, той же розробник, який відхилив криву 2 (рис. 4.3) в іншій ситуації (володіючи іншою інформацією, перебуваючи в іншому оточенні або в іншому емоційному стані), міг оцінити характеристику 2 як задовільну.

148

4.2.3. Способи оцінки технічних систем

Розглянемо два основних способи оцінки технічних систем, які визначають і постановку задачі, і значною мірою структуру алго­ритму синтезу.

Перший спосіб пов'язаний з розрахунком певного набору чисел та функцій. При цьому кожній із систем відповідає одна й та ж множина чисел і функцій, хто б і коли їх не розраховував та неза­лежно від умов розрахунків.

В останньо­му прикладі набір чисел і функцій складався з одного елемента 8 .

Після того, як числа і функції визначені, пе-

і

ревіряється вико­нання системи нерівностей або інших подібних

_ . . _ _ . .. . співвідношень.

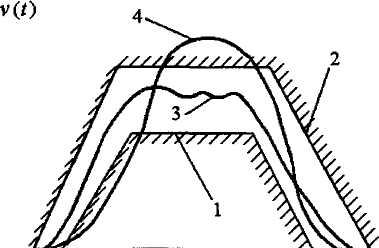
Рис. 4.4. Задання області, до якої повинні на- _{Така пере}вірка

лежати характеристики всіх систем, _{з и т}/ ^_о.

що синтезуються _{значно приводать}

або до придатності системи, або до її непридатності. В розглянутому прикладі 4.6 достатньо було з'ясувати справедливість однієї нерівності (4.8). У більш складних випадках може виявитися не­обхідність перевірки, чи належить якась характеристика створюва­ної системи завчасно вказаній області. Наприклад, розробник може вимагати, щоб характеристика V (і) всіх придатних варіантів систе­ми містилась у завчасно вказаній області (рис. 4.4). Тоді оцінка при­датності системи зводиться до поточкової (для кожної абсциси І, розміщеної між ?о і 11) перевірки приналежності числа у(і) відповідному відрізку, який обмежений ламаними 1 і 2 (рис. 4.4). Ви­ходячи з такого способу оцінки технічних систем, характеристика З задовольняє вказані вимоги, а характеристика 4 — ні.

Такий жорстко формалізований, однозначний, що не допускає ніяких неформальних моментів, підхід називають карди-налістським підходом до синтезу технічних систем [26].

149

_І

Другий спосіб . Альтернативним до розглянутого способу _Оц-нки технічних систем є ординалістська трактовка синтезу [26]. -рг" передбачається, що неможливо (недоцільно) використовувати дт/ оцінки технічних систем тільки набір чисел і функцій або на основ цього набору неможливо (недоцільно) завжди й однозначно дават' висновок про придатність системи.

До цих пір ми вважали, що мета синтезу полягає в знаходженні опису придатної (задовільної) системи. Такий підхід відповідає не­оптимальному синтезу технічних систем.

Однак у багатьох випадках розробник хоче досягти макси­мальної мети — йому потрібна не задовільна, а найкраща з усіх можливих систем. Така стратегія проектування приводить до опти­мального синтезу.

Неважко здогадатися, що оптимальний синтез неможливо ви­конати, якщо ми обмежимося винесенням рішення про за­довільність, але не зуміємо зрівняти хоча б дві технічні системи, щоб вибрати з них кращу. Нехай запропоновано для порівняння дві технічні системи з певного набору і ми можемо зробити один з трьох висновків: перша система краща, ніж друга; друга система краща першої; з точки зору їх використання системи однакові (еквівалентні).

При кардиналістському порівнянні цих систем, оперуючи пев­ним набором чисел і функцій, а також алгоритмом їх обробки, зав­жди та однозначно можна прийняти одне й тільки одне із трьох рішень. В ординалістському варіанті використання набору чисел і функцій, як і алгоритмів їх обробки, не забороняється. Однак тут не вказується ніякого формального правила, за допомогою якого мож­на зробити однозначний висновок про перевагу тієї чи іншої систе­ми і який не залежав би від неформальних обставин, кваліфікації, досвіду та смаків експерта тощо.

Типовим прикладом кардиналістської оцінки може бути рішення віддати перевагу системі (приклад 4.6) з меншим 8 (рис. 4.3). Ординалістський шлях порівняння систем здійснюється експер­том на основі вивчення графіків типу тих, які показано на рис. 4.3. Наприклад, експерт може віддати перевагу системі з характеристи­ками у(і), що не мають значних виступів, хоча їх відхилення від ідеальної характеристики були б значними.

150

4.2.4. Неоптимальний і оптимальний синтез технічних систем

Розглянемо суть неоптимального та оптимального автоматизова­ного синтезу технічних систем з використанням ЕОМ. Нехай опис по­ведінки, характеристик і властивостей системи зводиться до задання п дійсних чисел К\,К.2,---,К_п— показників якості (функціонування) технічної системи. Кардиналістські рішення про задовільність і перевагу тих чи інших систем повністю можуть бути зведені до обробки цих п чисел, які утворюють деякий вектор К. В ординалістському трактуванні цей вектор також може виявитися корисним, хоча не повинен алго­ритмічно приводити до однозначних рішень.

Неоптимальний кардиналістський синтез. Він полягає в перетво­ренні описів впливів, необхідної поведінки, характеристик і властиво­стей системи в такий опис бажаної системи, для якої одночасно вико­нується п нерівностей:

к_п<к_х<к\,

(4.9)

к_пі<к_п<к¹

} (і =

Дійсні числа Кц та АГ_г- (і = 1, 2,..., я) задаються разом зі складом век­тора К. Деякі з чисел Кц або всі вони можуть бути і нулями. Наприк­лад, для механічної системи (приклад 4.7) нерівності (4.9) можуть прий­няти такий вигляд:

>' = 1,2,

<е\

п₂)\

< V • (і = 1 2 п V

<,РІ (7 = 1,2, ...,п_р\ < й) (нерівність з номером и-1),

(4.10)

151

< М (нерівність з номером гі). Тут О{- напруження для /-го елемента конструкції. Абсолютна ве­личина напруження не повинна перевищувати (7,- (всього таких умов п_о); 2;, V і, м> ;- переміщення, швидкість і прискорення в де-якій у-й точці, абсолютні величини яких не повинні перевищувати граничних значень 2 :, V ,-, м> і (таких умов п₂); Р% - зусилля в &-

му елементі конструкції, яке обмежується величинами Рк (число цих нерівностей Пр може дорівнювати п_а). Передостання з нерівностей (4.10) вимагає, щоб основна частота (й не була меншою від деякого граничного значення (О\, а остання нерівність обмежує масу М конструкції.

Необхідно відзначити, що в нерівностях типу (4.9) часто наявні вимоги до надійності (наприклад, до напрацювання на відмову) і техніко-економічні (наприклад, обмеження зверху на вартість систе­ми).

Найчастіше машинний синтез використовується після того, як знайдена структура системи і вибрано базис її елементів. Тоді задо­вольнити нерівності (4.9) - (4.10) можна, лише змінюючи вектор а, від якого залежать усі К\, Л^,..., К_п.

Кардиналістський підхід до синтезу полягає в тому, що кожна

система однозначно характеризується набором чисел з вектора К. Рішення про задовільність системи вимагає перевірки, чи задоволь­няє кожний з компонентів цього вектора відповідну нерівність (4.9). Такий алгоритм синтезу не допускає ніяких неоднозначностей. Він допускає лише неоднозначність результату — може статися так, що задовільними є декілька систем. Розглянутий підхід синтезу не вка­зує алгоритму, за яким необхідно вибрати той чи інший варіант сис­теми з отриманих задовільних варіантів.

Неоптимальний ординалістський синтез. Тут відсутній формальний алгоритм прийняття рішення про задовільність варіанта технічної системи. Можливий синтез системи, коли для '» оцінки відсутній набір функцій і чисел. Однак такий підхід не­доцільний та не використовується в практиці створення технічних систем. Більш доцільним є спосіб, коли для оцінки систем зберігається набір чисел і функцій, але процес вибору складу векто-

152

ра К і крайніх меж Кц та Кі у нерівностях (4.9) здійснюється кон­структором неформально. Розглянемо це на прикладі.

Приклад 4.9. При оцінці механічної системи, критерії за­довільності якої виписані у вигляді (4.10), можуть у деяких випадках виключати окремі нерівності або доповнювати систему новими

нерівностями. Величини а і, 2.), V' р иЛ-, р\, (й\,М конструктор

може змінювати, виходячи з нової інформації, яку він отримав до певної стадії синтезу.

Вектор параметрів а , від якого залежать компоненти вектора К, повинен задовольняти певні обмеження. Неприклад, маси тіл та їх розміри повинні виражатися додатніми числами і не бути більшими за граничні значення. Цю умову можна сформулювати так: вектор а повинен належати деякій області в просторі пара­метрів О_а.

Оптимальний кардиналістський синтез. Вважаємо, що характеристики й властивості системи достатньо повно відображаються вектором К.

При оптимальному підході до синтезу системи частина компо­нентів, як і при неоптимальному синтезі, повинна задовольняти сис­тему нерівностей (4.9). Інша частина складових повинна приймати мінімальні або максимальні значення, тобто

(4.Ц)

К ₅=

Розглядаючи замість складових К, які повинні приймати макси­мальні значення, ті ж складові зі знаком мінус або зворотні ве­личини, легко виключити із системи (4.11) умови максимуму. На­приклад, замінивши К_п+2 на — К_п+2, отримаємо

К_п+1= тіп, К= тіп,

(4.12)

К ₃= тіп.

_І

153

Умови (4.12) називаються екстремальними, а нерівності (4.9) — ₀§. меженнями в задачі оптимального синтезу технічної системи. При цьому вектор параметрів а повинен належати множині значень 5

Оскільки компоненти вектора К є функціями від а і характе­ризують цілі синтезу, то Кі(аі,...,а_р) часто називають цільовими

функціями. Вирази системи (4.12) називаються критеріями опти-мальності. Задача оптимального синтезу в такій постановці вва­жається розв'язаною, якщо знайдено хоча б один вектор а такий що він сам належить С _а, а показники якості, які йому відповідають, задовольняють вимоги (4.9) і (4.12).

Оптимальний ординалістський синтез. Співвідношення між цим підходом і тільки що розглянутим приблизно таке ж, як при неоптимальному синтезі. Як і там, перед розробником відкриваються два шляхи.

1. Можна розрахувати деякі числа, функції, побудувати якісь графіки та вважати, що вся ця інформація досить повно характери­ зує систему, яка створюється. Такі розрахунки і такі побудови по­ вторюються декілька разів у процесі зондування системи або її на­ правленого вивчення. Потім розробник вивчає ці набори чисел і графіків для різних варіантів побудови системи. В результаті такого вивчення він робить висновок, яка з систем найкраща, оптимальна. Інший або навіть той же розробник в інших умовах може прийняти інший варіант системи — в цьому виявляється неформальність ор- диналістського підходу до синтезу технічних систем.

2. Можна прийти до прийняття рішення при ординалістському синтезі і більш формально, використовуючи більш вільну трактовку кардиналістських умов (4.12) та факту належності вектора а до об­ ласті С_а. У процесі синтезу допускається змінювати склад нерівностей (4.9) і набір критеріїв (4.12), переводити компоненти ве­ ктора К із (4.12) у (4.9) і навпаки або знехтувати якимись з них, де­ формувати область С_а й змінювати межі Кц та К _г- у нерівностях

(4.9).

У багатьох випадках такий ординалістський підхід виявляється більш корисним і порівняно з досить вільним ординалістським підходом, і порівняно з кардиналістським підходом.

4.2.5. Алгоритм неоптимального синтезу технічних систем

До цього розглядалися, в основному, проблеми постановки задачі синтезу та їх вирішення, виходячи із загальних принципів,

154

якими можна користуватися при знаходженні описів технічних сис­тем. Тепер розглянемо деякі конкретні способи синтезу, які базують­ся на жорстко алгоритмізованих крадиналістських підходах.

Нехай цілі створення нової системи й висунуті до неї вимоги добре відомі розробнику, і він може визначити показники якості К\,К2>---,К_п, які повністю описують систему, і можна вказати

межі Кц,К\,..., К_п\,К_п, в яких відповідні показники повинні

знаходитись. Кардиналістська постановка задачі породжує абсо­лютно жорсткі вимоги до майбутньої системи. В обмін на це роз­робник отримує можливість перекласти весь процес синтезу технічної системи на ЕОМ, оскільки ніяких неформальних рішень, що пов'язані зі зміною постановки задачі, йому приймати не дове­деться, хіба що в такій постановці розв'язати проблему синтезу вза­галі не вдається.

Процес синтезу розпадається на ряд стадій. Перші з них пов'язані з синтезом структури і вибором базису елементів, тобто набору елементів, із яких будуються системи. Ці стадії погано піддаються формалізації, і, як правило, виконуються людиною при допомозі ЕОМ. Однак покажемо, як міг би бути алгоритмізований синтез структури, або, як його ще називають, структурний синтез.

Нехай перетворення деякого входу и(ґ) у вихід у (і) у довільній за фізичною природою системі здійснюється всього лише трьома блоками А, В, С і кожен з них розміщується за іншим так, як показано на рис. 4.5 (приклад 4.8). Кожний із блоків А, В, С може займати будь-яку позицію 1, 2, 3.

"(О

1		2		3

У (0

Рис. 4.5. Структура системи, що синтезується: 1, 2, 3 — номери блоків системи

У цій дуже ідеалізованій ситуації на кожен із блоків можна дивитися як на неподільний елемент системи. В сукупності блоки А, В, С скла­дають базис елементів синтезу. При цьому ми вважаємо, що мікроструктура кожного блока вибрана і фіксована, але їх парамет­ри не визначені та є вільними. Позначимо відповідні сукупності па­раметрів блоків через п_А, п_в, п_с.

155

До чого в таких умовах зводиться синтез системи? По-перщ_е до вибору порядку розміщення блоків А, В, С: можливі структури АВС, ВСА, САВ, СВА, ВАС, АСВ. По-друге, до знаходження всіх

компонентів вектора п, тобто до знаходження "підвекторів" а

п_в, п_с. Результат останнього розрахунку повинен залежати від по­рядку розміщення блоків. Тому визначення параметрів, яке нази­вається параметричним синтезом, не може бути ізольовано від син­тезу структури.

До початкової інформації в кардиналістському неформально­му синтезі належать: опис структур елементів (у нашому прикладі блоків А, В, С); опис області С_а, до якої можуть належати допус­тимі значення набору параметрів п , тобто об'єднання наборів а ,

п_в, п_с; 2л чисел К \_І5 К\,..., К_П\,К_П, які входять у нерівність (4.9)

і визначають уже сформульовані умови прийнятності системи, що синтезується.

Відомо, що синтез становить перетворення одних описів в інші. Описи, які нам треба знайти, такі: трьохелементна послідовність символів, що розміщує в певному порядку букви А, В, С — це опис структури системи; набір чисел п, тобто опис пара­метрів системи. Задача синтезу буде розв'язана, якщо описи, що зна­ходяться в початковій інформації, виявляться перетвореними в останні два.

Алгоритм синтезу можна розділити на наступні етапи.

1. На основі інформації про подібні системи й спираючись на досвід та інтуїцію конструктора або випадково, останній видає пев­ ну послідовність символів А, В, С і деякий початковий вектор пара-

метрів и . Цим повністю визначається система, якщо дотримува­тися початкових припущень.

2. Проводиться частковий аналіз системи, що вибрана на по­ передньому етапі. Такий аналіз обмежується розрахунком вектора К.

3. Здійснюється перевірка п нерівностей (4.9) і формується вис­ новок про задовільність чи незадовільність системи.

Якщо система виявилась задовільною, то процес неоптималь­ного синтезу можна вважати вдало завершеним. Якщо нерівності (4.9) не виконані, то здійснюється новий процес підбору задовільної системи. Цей процес здійснюється шляхом повернення до першого

156

етапу при наявності інформації про попередню незадовільну систе­му-

Можливі варіанти алгоритму синтезу відрізняються стратегією вибору в цих умовах нової системи. Тут можна йти двома напря­мами. Перший — зберегти попередню структуру системи , тобто послідовність блоків, і постаратися задовольнити умови придатності системи за рахунок більш вдалого вибору вектора параметрів п, ніж у попередньому випадку, коли інформації було менше, ніж за­раз. Це, по суті, намагання вийти з положення за рахунок парамет­ричного синтезу. Другий — вважати, що незадовільність системи за­лежить від поганої структури, і тому подальші пошуки в просторі параметрів дають мало шансів на успіх. Тоді структура змінюється, тобто вибирається нова послідовність елементів А, В, С і в цій стру­ктурі вибирається нова комбінація параметрів — вектор п .

Якщо в нових умовах на першому етапі нова система так або інакше вибрана, то можна перейти до етапу 3 і проаналізувати на задовільність отриману систему. При цьому можливі два варіанти: або запропонований алгоритм синтезу приведе до задовільної сис­теми, або обчислювальні ресурси будуть вичерпані до того, як це станеться (в подібних циклічних розрахунках часто встановлюється певний граничний час, і ЕОМ автоматично закінчує розрахунок, як тільки відведений час використано). В другому випадку розробнику необхідно замінити початкову інформацію, розширити обмеження на структуру або перейти до нового алгоритму синтезу.

Подібні розв'язки вимагають високої кваліфікації розробника. Перехід до нового алгоритму базується на впевненості, що задача синтезу в її початковій кардиналістській постановці може бути розв'язана, але використаний раніше алгоритм або не знаходить розв'язку, або розшукує його недопустимо повільно, Можливий та­кож варіант, що не існує жодної структури й жодної комбінації па­раметрів, які дають змогу задовольнити п нерівностей (4.9). Тоді всі подальші намагання приведуть до невдачі і обчислювальні ресурси будуть використані марно.

4.2.6. Правила зміни структури і параметрів технічних сис­тем

Правила зміни структури можуть базуватися на двох різних ідеях. Перша полягає в довільному переборі всіх можливих струк­тур. Це, по суті, зондування структурного простору. Друга ідея вра­ховує інформацію, що накопичилась на останньому або декількох

157

попередніх спробах синтезу. Нехай у першій серії спроб останнього прикладу 4.8 була структура АВС і намагання знайти для неї такі параметри, щоб система стала задовільною, виявились без­успішними. Алгоритм подальшого пошуку структури може будува­тися з урахуванням невдачі в першій спробі. З неї, наприклад, може випливати, що А не повинно бути першим блоком. Тоді структуру АСВ можна не розглядати і таким чином зменшити кількість спроб синтезу структури системи.

Такі алгоритми можуть базуватися лише на глибокому ро­зумінні того, як функціонує система, як структура першого блоку впливає на вектор показників К усієї системи і т. д. Зрозуміло та­кож, що невдача пешої спроби може бути пов'язана з двома наступ­ними блоками і подальший синтез системи в просторі структур буде направлено по хибному шляху.

Необхідно відзначити, що структурний синтез вимагає значних зусиль та витрат, бо його перспективність стає зрозумілою тільки тоді, коли закінчено і параметричний синтез. Оскільки структури містять, як правило, досить велику кількість елементів, то вимоги до обчислювальних засобів бувають досить значними.

Алгоритмічні пошуки структури системи пов'язані зі значними труднощами. їх можна порівняти, наприклад, з пошуком найкращо­го наступного ходу в шаховій партії. Для них характерні і вимушена відмова від довільного перебору всіх варіантів, і необхідність кількісно оцінити значну й важко формалізовану накопичену інформацію, і проблема прогнозу тих наслідків, до яких може при­вести прийняте рішення. Такі задачі зараз інтенсивно досліджуються, і, можливо, з часом перспективи алгоритмічних пошуків структури будуть більш реалістичними, ніж сьогодні.

Ситуація з правилами зміни параметрів при синтезі технічних систем значно спрощується. В цій задачі структура системи відома, залишається знайти такий вектор а, щоб були виконані п нерівностей (4.9). Оскільки в усіх відношеннях, крім вибору вектора,

система описана, то відомі і правила обчислення вектора К.

Отож, формально кажучи, необхідно розв'язати деяку систему нерівностей. Розв'язуванням цієї задачі займається спеціальна галузь математики. Покажемо, як поєднати розв'язування системи нерівностей із задачею знаходження екстремуму деякої спеціально підібраної функції. Таке зведення однієї проблеми до іншої поєднує

158

між собою неоптимальний і оптимальний параметричний синтез систем. Пояснюється це тим, що багато задач оптимального синтезу також зводяться до знаходження екстремуму.

Для простоти обмежимось випадком, коли показників якості системи всього два (п = 2). Тоді необхідно знайти вектор а такий, щоб виконувалося дві нерівності:

К_п<К_х(а)<к\, К₂₁<К₂(а)<К¹₂. (4.13)

При цьому вектор параметрів зобов'язаний належати області С_а, яка вже вказана.

Перетворимо дві двосторонні нерівності (4.13) в чотири одно­сторонні:

К_х(а)-К\<0; К_іг-К_х{а)<Ь;

(4.14)

К₂ (а) - К₂< 0; К₂₁- К₂ (а) < 0.

Якщо позначити тепер ліві частини нерівностей (4.14) через /\(а),..., /4(0), то отримаємо еквівалентну (4.14) систему:

Л(а) < 0,

(4.15)

/₄(а) < 0.

Із чотирьох функцій зліва в (4.15) побудуємо одну Р(а) за прави­лом

\<і<4 Цей запис означає, що для кожного значення а обчислюються

чотири значення /\(а), /2(а)> /з(^)> І^Ф) ^и ^РЗД них виби­рається найбільше — воно і приймається рівним Р(а) ■ Якщо тепер знайти такий вектор а \, щоб було

/^г(а₁) = ГПІП (4.17)

і вектор а і належав С_а, то знайдене значення а і буде задовольня­ти початкові нерівності (4.13), а з ними і (4.14) та (4.15).

159

це гіпотетичних

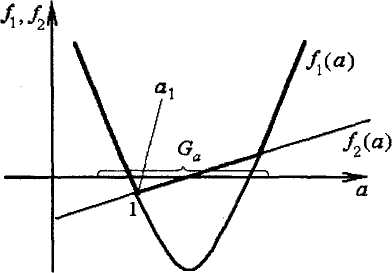
Рис. 4.6 ілюстру_є на прикладі двох функцій від однієї

Рис. 4.6. Зведення системи нерівностей до

розв'язання задачі пошуку мінімуму

(жирна ламана)

змінної (параметра) а (приклад 4.9). Легко бачити, що знайдене та­ким чином значення (точка 1) задовольняє всі нерівності (хоча це і не єдина точка зору). У всякому разі бачимо, що, вміючи розв'язувати задачі мінімізації, які пов'язані з оптимальним кардиналістським син­тезом, можна реалізувати і процес неоптимального синтезу.

4.3. Морфологічний аналіз і синтез технічних систем

Метод морфологічного аналізу та синтезу, розроблений швей­царським астрономом Ф.Цвіккі, побудований на принципах комбінаторики [27]. Суть його полягає в тому, що в технічній сис­темі або в іншому об'єкті виділяють групу основних конструктивних або інших ознак. Для кожної ознаки вибирають альтернативні варіанти, тобто можливі варіанти його реалізації. Комбінуючи їх між собою, можна отримати множину різних технічних рішень, у тому числі і тих рішень, які мають практичний інтерес.

Практичне використання методу полягає в побудові морфо­логічної таблиці, заповненні її можливими альтернативними варіантами та виборі із всієї множини найбільш прийнятних технічних рішень.

Найбільше поширення отримав метод Цвіккі, в якому за озна­ки вибираються функції елементів технічної системи, а за альтерна­тивні варіанти — різні способи реалізації кожної функції. В цьому випадку морфологічна таблиця буде мати стільки стовпців, скільки функціональних елементів в системі на вибраному рівні. Тоді кількість можливих варіантів технічних рішень визначається за­лежністю

160

де т - число функціональних елементів системи на заданому рівні; уц- число альтернативних варіантів г-го (і = 1, 2,..., пі) функціонального елемента.

Розглянемо побудову морфологічної таблиці на прикладі стрілової системи вантажопідйомного крана з горизонтальним пе­реміщенням вантажу при зміні вильоту (рис. 4.7).

Стрілова система складається з таких основних

функціональних еле-

2 ^^^®| ментів: 1 - стріловий

Рис. 4.7. Схема стрілової системи крана

п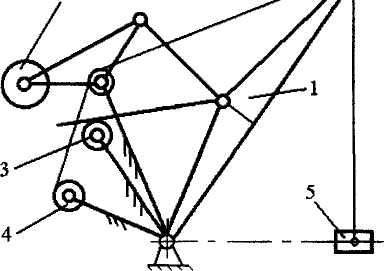 ристрій; 2 - механізм його врівноваження; 3 -приводний механізм; 4 -механізм вирівнювання траєкторії вантажу 5. Для розглянутої системи морфологічна таблиця має чотири стовпці, в які входять функціональні елементи стрілової сис­теми (табл. 4.1). У цій же таблиці в кожному стовпці приведеш альтернативні варіанти функціональних елементів стрілової систе­ми.

Шляхом вибору одного з альтернативних варіантів технічних рішень з кожного стовпця отримаємо один із можливих варіантів стрілової системи. Так, якщо взяти альтернативні варіанти під пер­шим номером із кожного стовпця, то отримаємо варіант стрілової системи, який показано на рис. 4.7.

Усього ж з цієї таблиці можна отримати N = 6-5-6-5=900 варіантів стрілової системи вантажопідйомного крана з горизон­тальним переміщенням вантажу. Ця таблиця може доповнюватися новими можливими варіантами функціональних елементів.

161

Таблиця 4.1 системи ван-

Морфологічна таблиця можливих варіантів стрілової тажопідйомного крана

	Функціональні елементи
Аль-тер-натив-ні варіа­нти	Стріловий пристрій	Механізм врівнова­ження	Приводний механізм	Механізм вирівнюван­ня траєкторії вантажу
1	Жорстка прямо­лінійна стріла	Чотири-ланковий	Рейковий	Профільний барабан
2	Жорстка криво­лінійна стріла	Шести-ланковий	Гвинтовий	Вирівнюва-льний блок
3	Шарнірно-скла­дова стріла з прямолінійним хоботом	Поліспа­стовий	Гідравліч­ний	Вирівнюва-льний поліспаст
4	Шарнірно-скла­дова стріла з профільним хо­ботом	На стрілі	Криво­шипний	Вантажний канат, пара­лельний осі стріли
5	Прямолінійна стріла з висув­ними секціями	Урівнова-жувальний візок	Поліспас­товий	Вантажний канат, пара­лельний осі відтяжки
6	Прямолінійна стріла із встав­ними секціями	—	Криво-шипно-коромис-ловий	—

Розглянемо процес складан­ня морфологічної таблиці на більш низькому рівні для привод­ного механізму стрілової системи вантажопідйомного крана. Одним із варіантів приводного механізму може бути рейковий механізм (рис. 4.8). Цей приводний меха­нізм складається з двигуна - 1, пе­редавального механізму - 2, з'єднувального пристрою - З, Рис. 4.8. Кінематична схема рейко- гальмівного механізму - 4 та рей-вого приводного механізму кового механізму -5.

162

Таблиця 4.2

Морфологічна таблиця можливих варіантів приводного механізму стрілової системи вантажопідйомного крана

Альтер­нативні варіанти	Функціональні елементи
	Двигун	Переда­вальний механізм	З'єдну­вальний пристрій	Гальмів­ний механізм	Виконав­чий механізм
1	Електро­двигун по­стійного струму	Цилін­дричний редуктор	Втулочно-пальцева муфта	Колодко­вий 3 електро­магнітним штовхачем	Зубчастий
2	Електро­двигун змінного струму з коротко-замкнутим ротором	Плане­тарний редуктор	Зубчаста муфта	Колодко­вий 3 гідравліч­ним штовхачем	Цівковий
3	Електро­двигун змінного струму з контакт­ними кільцями	Черв'яч­ний редуктор	Лацюгова муфта	Стрічковий з важель-ним про­стим керу­ванням	Черв'яч­ний
4	Гідродвигун	Хвильо­вий ре­дуктор	Кулачко­во-дискова муфта	Стрічко­вий дифе­ренціаль­ний	Гвинто­вий
5	Двигун внурішньо-го згоряння	Конічний редуктор	Гідро­муфта	Дисковий	Поліспас­товий
6	—	Комбі­нований редуктор	Глухе фланцеве з'єднання	Порошко­вий елетро-магнітний	Рейковий
7	—	—	Кулачко­вий	Електро- індукцій-ний	Криво-шипно-короми-словий

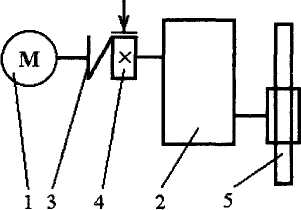
У приводному механізмі виділено п'ять функціональних елементів, різні альтернативні варіанти яких утворюють морфологічну табли­цю (табл. 4.2).

163

Аналіз табл. 4.2 показує, що можна отримати N = 5 • 6 • 7 • 7 • 7 = 10290 варіантів приводу зміни вильоту стрілової си­стеми. Не всі ці варіанти приводу можуть мати практичне втілення. Однак значна кількість альтернативних варіантів дає змогу провести аналіз різних конструктивних рішень і вибирати з них у тих чи інших умовах найбільш ефективні та перспективні конструкції при­водів.

164

5. КЕРУВАННЯ ТЕХНІЧНИМИ СИСТЕМАМИ 5.1. Поняття керування

Питання про керування в складних технічних ситемах різної фізичної природи мають в останні роки все більше і більше значення. Це пов'язано з тим, що для технічних систем, які мають справу з високими енергіями, значними швидкостями, швидкоплин­ними процесами, дорогими установками й експериментами, харак­терна вимога найбільш раціонального використання ресурсів, вибо­ру найкращих можливостей програми дій. Усе це визначає ті про­блеми, які становлять предмет теорії керування.

У технічних системах проходять процеси, характер яких зале­жить від множини супутніх їм умов та факторів. Змінюючи умови проходження процесів, можна впливати на їх характер, змінювати їх, пристосовувати їх до тих або інших цілей. Таке втручання в при­родний хід процесу, зміна його і являють собою суть керування. Та­ким чином, можна сказати, що керування становить таку ор­ганізацію того або іншого процесу, яка забезпечує досягнення пев­них цілей [28].

Будь-який процес керування можна розділити на чотири ета­пи: поява мети, оцінка ситуації, прийняття рішення і реалізація прийнятого рішення. Етап появи мети з'являється до початку проце­су керування, тому його можна не розглядати. В зв'язку з цим про­цес керування можна розглянути як виконання трьох основних етапів:

1)збір та обробка інформації з метою оцінки ситуації, що склалась;

2. прийняття рішення про найбільш цілеспрямовані дії;

3. виконання прийнятого рішення.

Інколи буває необхідним ще четвертий етап: контроль вико­нання рішення.

Різні види задач керування відрізняються один від одного спо­собом і послідовністю виконання цих операцій.

Існує багато задач, у яких механізми збору та обробки інформації та виконання прийнятого рішення відпрацьовані досить чітко, що над ними можна зовсім не замислюватися при здійсненні процесу керування. В таких задачах всі розглянуті процеси керуван­ня зводяться, по суті, до розгляду тільки другого етапу. Подібні за­дачі називають одноетапними задачами прийняття рішення.

165

До промислової революції керівництво дрібним підприємством могла здійснювати одна людина, яка здійснювала закупки, планувала і направляла роботу, збувала продукцію, найма­ла й звільняла робітників. При малих розмірах підприємства керівник міг приймати організаційні рішення, не використовуючи ніяких наукових методів та базуючись лише на своїх знаннях, досвіді, інтуїції. Якщо деякі з прийнятих рішень були не кращими, то вони не приводили до значних втрат або могли бути швидко ви­правлені.

Укрупнення промислових підприємств зробило неможливим здійснення адміністративних функцій однією людиною. З'явились керівники виробничих відділів, відділів збуту, фінансових відділів, відділів кадрів і т. д. Механізація й автоматизація виробництва привела до подальшого розчленування адміністративних функцій. Так, виробничі відділи виявились поділеними на більш дрібні гру­пи, які займаються питаннями експлуатації та ремонту, контролю якості, планування, постачання, зберігання готової продукції тощо.

Кожний окремий спеціалізований підрозділ великої організації виконує певну частину спільної роботи, керуючись загальними цілями підприємства. Однак у кожного спеціалізованого підрозділу виникають і свої власні цілі. Всі ці цілі не завжди узгоджуються, а інколи вступають у протиріччя між собою.

Як приклад можна розглянути проблему забезпечення підприємства запасами. Окремий підрозділ може бути зацікавлений у значному збільшенні запасів на складі для забезпечення непере­рвного випуску своєї продукції. Але при обмеженому об'ємі складських приміщень це приводить до зниження запасів для інших підрозділів. У результаті виникає задача організаційно-управлінського типу — вибір такої стратегії у відношенні запасів, яка була б найбільш доцільна для всього підприємства в цілому.

При розв'язуванні подібного роду організаційно-управлінських задач необхідно дуже добре розуміння цілей окремих підрозділів і таке їх погодження, щоб вони не вступали в протиріччя ні між собою, ні із загальними цілями всього підприємства. Якщо при цьому врахувати, що прийняття некращих рішень в умовах ве­ликого підприємства може принести немалі збитки, то стає ясно, що при розв'язуванні організаційно-управлінських задач стає недопус­тимим базуватись тільки на особистому досвіді й здоровому глузді. Необхідні наукові методи.

Розробкою наукових методів розв'язування організаційно-управлінських задач займається наукова дисципліна, яка отримала назву дослідження операцій. Під операцією розуміють деякий ор-

167

Однак такий підхід у більшості випадків є ідеалізованим і спрощенням реального керування. В дійсності всі етапи процесу ке­рування знаходяться в тісному взаємозв'язку і етап прийняття рішення вимагає детального розгляду можливих способів реалізації прийнятого рішення.

Інколи процес керування розбивають на декілька послідовних кроків, причому рішення, прийняте на будь-якому кроці, залежить від результатів виконання рішень попереднього кроку. Прикладом може бути процес керування складною системою, якою є ракета (при запуску її із Землі на Місяць). Тут важливо виділити наступні кроки: виведення ракети на навколоземну орбіту, організація руху ракети в напрямку Місяця, перехід ракети на навколомісячну орбіту, посадка ракети на Місяць.

У цьому прикладі окремі кроки процесу керування виявилися досить природними. Однак у багатьох випадках розбивання склад­ного процесу керування на кроки з чітким виділенням усіх його етапів на кожному кроці виявляється досить складною задачею.

Із розглянутого бачимо, наскільки складними і різноманітними можуть бути задачі керування. Однак значною мірою можна недооцінити складність розв'язування цих задач, якщо враховувати ті обставини, що процеси керування проходять, як пра­вило, в складному навколишньому оточенні. На здійснення процесів керування впливають різноманітні зовнішні фактори, сукупність яких часто називають станом природи. Для того, щоб прийняти правильне рішення про ті або інші дії, необхідно оцінити результати цих дій, а для цього необхідно знати характер ситуації, в якій ці дії здійснюються.

Однак типовим для задач керування є випадок, коли наявна інформація буває або недостатня для точної оцінки ситуації, або викривлена зовнішніми факторами. При цьому недостатність інформації не знімає задачі прийняття рішення. Особливість задач керування саме в тому і полягає, що рішення повинно бути обов'язково прийняте незалежно від того, в змозі ми точно оцінити результати, до яких приведе прийняте рішення, чи ні.

Таким чином, у процесі керування виникає важлива зада^ча прийняття рішення в умовах, коли інформація про ситуацію, то склалась, або недостатня, або викривлена. Така задача отримала назву задачі прийняття рішення в умовах невизначеності.

Розглянемо ще один специфічний клас задач керування, який пов'язаний із діяльністю великих промислових підприємств, на зра зок організаційно-виробничої технічної системи, яка була розгляну та в другому розділі.

166

теріали до об'єкта будівництва можна, користуючись залізничним, водним та автомобільним транспортом. Розв'язком задачі буде вибір найбільш вигідного виду транспорту з точки зору часу дос­тавки, вартості, збереження властивостей матеріалів тощо. Ана­логічний стан має місце і в задачах керування технічними ситемами.

У тих випадках, коли мета керування може бути досягнута декількома різними способами, на спосіб керування можна накласти додаткові вимоги, ступінь виконання яких може служити основою для вибору способу керування.

У багатьох випадках реалізація процесу керування вимагає витрат тих чи інших ресурсів, електроенергії і т. п. Отже, при виборі способу керування необхідно говорити не тільки про те, чи дося­гається поставлена мета, але й про те, які ресурси доведеться витра­тити для її досягнення. В цьому випадку задача керування полягає в тому, щоб із множини рішень, які забезпечують досягнення постав­леної мети, вибрати одне, що вимагає найменших витрат ресурсів.

В інших випадках основою для вибору способу керування мо­жуть бути інші вимоги, що накладаються на систему керування: вартість обслуговування, надійність, відхилення отриманого стану системи від бажаного тощо.

Математичний вираз, який дає кількісну оцінку ступеня вико­ристання накладених на спосіб керування вимог, називають кри­терієм якості керування. Найбільш доцільним, або оптимальним. способом керування буде такий, при якому критерій якості керуван­ня досягає мінімального (максимального) значення. При виборі, на­приклад, режиму польоту ракети за критерій якості керування мож­на прийняти або вираз для кількості палива, яке витрачається на одиницю шляху, або шлях, котрий проходить ракета за рахунок одиниці палива. Найбільш економічному, тобто оптимальному ре­жиму руху буде відповідати в першому випадку мінімальне, а в дру­гому максимальне значення критерію якості керування.

Наведене визначення оптимального керування розглядатиме­мо як попереднє. Більш повне визначення буде наведено після роз­гляду обмежень, які накладаються на процес керування.

5.2.2. Обмеження, що накладаються на процес керування

Задачу знаходження оптимального керування або керування взагалі необхідно вважати неіснуючою, якщо на характер руху сис­теми не накладено ніяких обмежень. При розв'язуванні задачі керу-

169

ганізаційний захід, проведення якого передбачає певну чітко сфор­мульовану мету, наприклад, регламентацію збережуваних на складі запасів. Повинні бути задані умови, що характеризують обставини проведення заходу, зокрема потреби в запасах і обмеження на складські приміщення в розглянутому прикладі. Метою дослідження операцій є знаходження і наукове обгрунтування таких способів, проведення заходів, які в певному сенсі є найбільш вигідними.

Специфічна особливість задач організаційно-управлінського типу полягає в тому, що наслідки того або іншого способу їх вирішення можуть суттєво відобразитися на роботі всього підприємства. Тому прийняття кінцевого рішення завжди належить до компетенції відповідальної особи, адміністратора, який наділений відповідними правами і виходить за рамки дослідження операцій. Дослідження операцій має на меті дати в руки адміністратору обгрунтовані рекомендації до прийняття рішення.

Таким чином, дослідження операцій являє собою науковий на­прям, мета якого полягає в розробленні методів аналізу цілеспрямованих заходів (операцій) і об'єктивна порівняльна оцінка можливих рішень. Хоча дослідження операцій становить са­мостійний науковий напрям, при розв'язуванні окремих задач воно застосовує методи кібернетики.

5.2. Оптимізація процесу керування 5.2.1. Критерій якості керування

Задачу керування будемо розглядати як математичну. Однак, на відміну від багатьох інших математичних задач, вона має ту особливість, що допускає не одне, а множину різних рішень. Це пов'язано з тим, що в задачах керування існує, як правило, багато способів організації будь-якого процесу, які приводять до досягнен­ня поставленої мети. Так, при запуску ракети на Місяць можна виб­рати різні траєкторії для її польоту і т. п. Тому задачу керування можна було б ставити як задачу знаходження хоча б одного з мож­ливих способів досягнення поставленої мети. Однак така постановка питання буває недостатньою.

Якщо є множина рішень будь-якої задачі, то необхідно вести розмову про вибір такого рішення, яке з тієї чи іншої точки зору бу­ло б найкращим. Можна навести багато прикладів подібних задач. Так, існує багато способів для виготовлення ємкості з листа металу заданих розмірів. Розв'язком цієї задачі необхідно вважати отри­мання ємкості максимальної місткості. Доставляти будівельні ма-

168

вання неможливо не враховувати ті обставини, що рух будь-якої системи завжди підлягає різного роду обмеженням.

Для більш повного уявлення про обмеження розглянемо кон­кретний приклад керування автомобілем. Здійснюючи процес керу­вання, водій повинен рахуватися з тим, що автомобіль має обмежену потужність двигуна, а це значить, що він може везти лише обмеже­ний вантаж з обмеженою граничною швидкістю. Завдяки інерційності, швидкість автомобіля і напрямок руху можуть змінюватись лише з обмеженим прискоренням. Це значить, що не­можливо миттєво зупинити або миттєво змінити напрямок руху у випадку виникнення непередбаченої ситуації, і це, в свою чергу, об­межує швидкість руху. При виборі маршруту водій вимушений ра­хуватися з обмеженим запасом палива в баку і необхідністю попов­нення цього запасу в дорозі й ін.

У загальному випадку існує два види обмежень на вибір спо­собу керування [28]. Обмеженнями першого виду є самі закони при­роди, відповідно до яких здійснюється рух керованої системи. При математичному формулюванні задачі керування ці обмеження явля­ють собою алгебраїчні, диференціальні або різницеві рівняння зв'язку. Другий вид обмежень становить собою обмеження ресурсів, що використовуються при керуванні, або інших величин, які в силу фізичних особливостей якоїсь системи не можуть чи не повинні пе­ревищувати певних меж. Математично обмеження цього виду вира­жаються, як правило, у вигляді систем алгебраїчних рівнянь або нерівностей, які зв'язують змінні, що описують стан системи.

5.2.3. Постановка задачі оптимального керування

Задачу керування можна вважати сформульованою матема­тично, якщо: сформульована мета керування, що визначена через критерій якості керування; визначені обмеження першого виду, які являють собою системи диференціальних або різницевих рівнянь, що обмежують можливі способи руху системи; визначені обмеження другого виду, які становлять собою систему алгебраїчних рівнянь або нерівностей, що враховують обмеженість ресурсів або інших ве­личин, які використовуються при керуванні.

Спосіб керування, який задовольняє всі поставлені обмеження і зводить до мінімуму (максимуму) критерій якості керування, нази­вають оптимальним керуванням.

170

5.3. Класифікація задач оптимального керування 5.3.1. Однокрокові задачі прийняття рішень

В однокрокових задачах не розглядаються методи реалізації прийнятого рішення, тобто визначається не величина і характер ке­руючого впливу п, а безпосередньо значення змінної стану системи X, яке забезпечує найкраще досягнення мети керування.

Однокрокова задача прийняття рішення вважається заданою, якщо задані простір сукупності неконтрольованих зовнішніх фак­торів V із розподіленням імовірностей р(У) для всіх УєК,

простір станів (розв'язків) X і критерій якості прийняття рішення, який для цього випадку називають цільовою Функцією. В літературі замість терміна "цільова функція" використовують також назву "функція виграшу" або "функція втрат". Цільову функцію, що виз­начає в явному вигляді цілі керування, можна розглядати як вихідну величину у технічної системи. Цільову функцію, яка залежить від не­контрольованих зовнішніх впливів V і від стану технічної системи х , можна записати у вигляді

у = У(х,У). (5.1)

Розв'язок однокрокової задачі полягає в знаходженні таких хєХ, які зводять до мінімуму функцію у, тобто задовольняють умову

дЬ _ _

х ={х єХ у(х,у)} = тіп. (5.2)

Якщо стоїть задача не мінімізації, а максимізації функції у, то

_ *

вона не приводить ні до яких труднощів, бо якщо при х є х

функція у(х,у) досягає максимуму, то при тому ж х функція — у (х, V ) буде досягати мінімуму.

Існує ряд методів розв'язування однокрокової задачі прийнят­тя рішення. Застосування того чи іншого методу залежить від спосо­бу задання множини допустимих рішень х, від інформації про не-контрольований зовнішній вплив і від виду цільової функції у. Оз­найомимося з характеристиками цих методів.

Задачу називають детермінованою, якщо немає невизначеності у відношенні до неконтрольованого зовнішнього впливу. В де­термінованих задачах простір неконтрольованого зовнішнього впливу V складається тільки з одного елемента V , імовірність яко-

171

го дорівнює одиниці. В цьому випадку цільова функція буде залежа­ти від стану технічної системи

у = у(х) = у(х_ь...,Х„). (5.3)

Однокрокову детерміновану задачу називають класичною за­дачею оптимізації [29], якщо в ній мають місце обмеження

/і(х_ь...,х_п) = 0, і = \,...,т, т<п. (5.4)

У цій задачі необхідно знайти значення Х\,...,х_п, які задовольня­ють рівняння (5.4) і мінімізують функцію у(х\,...,х_п).

Однокрокові задачі отримали назву математичного програму­вання. Ці методи дають можливість знайти значення змінних Х\,...,х_п, які задовольняють обмеження

//*!,. .,х„Я = ЬіІ = 1,. ./и (5.5)

і перетворюють у мінімум цільову функцію у(Х[,...,х_п). На змінні часто накладають допоміжні умови невід'ємності їх значень. Не­обхідно відзначити, що математичне програмування являє собою не аналітичну, а алгоритмічну форму розв'язування задач, тобто дає не формулу, яка визначає кінцевий результат, а вказує лише обчислювальну процедуру, що приводить до розв'язування задачі. Тому методи математичного програмування стають ефективними, головним чином, при використанні ЕОМ.

Найпростішим випадком задачі математичного програмуван­ня є задача лінійного програмування. Вона відповідає випадку, коли ліві частини обмежень (5.5) і цільова функція (5.3) становлять лінійні функції від Х\,...,х_п. У задачі лінійного програмування необхідно знайти невід'ємні значення змінних Х\,...,х_п, які мінімізують цільову функцію

п У(Х₁,..._ІХ_П)=^С_ІХ_] (5.6)

7=1 і задовольняють систему обмежень

^а_і}х_]<Ь_і, / = 1,...,т. (5-7)

7=1

Будь-яку задачу математичного програмування, яка відрізняється від сформульованої, називають задачею нелінійного. програмування. В задачах нелінійного програмування або цільова

172

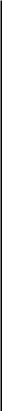функція (5.3), або ліві частини обмежень (5.5), або те й інше являють собою нелінійні функції від Х\,...,х_п. Однак до задачі нелінійного програмування відноситься і така, в якій цільова функція та обме­ження мають вигляд (5.6) і (5.7), але пропонується, наприклад, цілочисельність змінних. Ця остання задача одержала назву задачі цілочисельного програмування.

Однокрокову задачу прийняття рішень називають стохас-

тичною. якщо простір некерованих зовнішніх впливів V скла­дається більше ніж з одного елемента, так що відомим є не дійсне значення некерованих впливів V , а розподіл імовірностей р (у) на

просторі V .

Стохастичні задачі, які вимагають знаходження значень змінних, що задовольняють обмеження (5.5) і мінімізують цільову функцію (5.3), називають задачами стохастичного програмування. Однак у багатьох випадках шляхом іншого визначення цільової функції задачі стохастичного програмування можуть бути зведені до задач лінійного програмування. Оскільки некерований зовнішній вплив V є випадковою величиною із розподілом імовірностей р (у)

на просторі V , то і значення у(х,\?) при заданому х =(хі,...,х_п) також буде випадковою величиною з тим же розподілом імовірностей р (V) на просторі V . Тому в цьому випадку за цільову функцію доцільно прийняти математичне сподівання функції у(х, V) на просторі V .

Таким чином, для випадкових процесів цільова функція має вигляд

Оскільки У\(х) являє собою детерміновану функцію від X, то за­дача знаходження змінних Хі,...,х_п, які задовольняють обмеження (5.5) і перетворюють у мінімум цільову функцію (5.8), може бути розв'язана методами лінійного або нелінійного програмування.

Важливим випадком однокрокової стохастичної задачі прий­няття рішення є випадок, коли величини Х\,...,х_п можуть приймати лише кінцеву множину значень. Методами розв'язування таких за­дач займається розділ математики, який отримав назву "Теорія сто-хастичних рішень".

Останнім часом значну увагу приділяють задачам, у яких рішення приймається не однією особою, а декількома (наприклад,

173

двома), причому інтереси цих осіб протилежні. Прикладом може бу­ти задача переслідування, в якій відстань між тим, хто переслідує і тим, кого переслідують, залежить від рішень та дій обох цих осіб При цьому той, хто переслідує, зацікавлений у тому, щоб макси­мально скоротити цю відстань, а той, кого переслідують, у тому щоб зробити її по можливості найбільшою. Подібні задачі отримали назву конфліктних ситуацій, а методи їх розв'язування розглядають­ся в теорії ігор. Осіб, що приймають рішення, називають гравцями

Оскільки в конфліктній ситуації рішення кожним із гравців приймаються незалежно від рішень іншого гравця, при матема­тичному описі конфліктної ситуації простір рішень необхідно роз­глядати як прямий добуток двох множин X х2, де X = {.Х|,...,л:_л} - простір рішень першого гравця; X = {2і,...,2_т} - простір рішень другого гравця.

Елементи простору рішень X У.2 становитимуть пари виду (х,г),х єХ,2 є 2, тобто будуть визначатися рішеннями, які прий­має як перший, так і другий гравець. Для простоти вважаємо, що невизначеність у стані неконтрольованого зовнішнього впливу відсутня. Тоді цільова функція

У = у(х^2) _ (5.9)

залежить тільки від елементів простору X X 2 .

Протилежність інтересів гравців полягає в тому, що перший гравець, який робить вибір із множини X, намагається своїм вибо­ром мінімізувати цільову функцію, в той час як другий гравець, кот­рий робить вибір з множини X , намагається її максимізувати. Та­ким чином, суть конфліктної ситуації полягає в тому, що кожний гравець повинен прийняти найкраще зі своєї точки зору рішення, пам'ятаючи, що його суперник зробить те ж саме.

5.3.2. Динамічні задачі оптимізації керування

Серед задач керування значне місце займають задачі, в яких технічна система знаходиться в стані неперервного руху й змін під дією різних зовнішніх і внутрішніх факторів. Задачі керування таки­ми технічними системами належать до класу динамічних чяпяч керу.: вання.

Технічна система називається керованою, якщо серед діючих на неї різноманітних факторів існують такі, користуючись якими

174

можна змінити характер її руху. Як уже вказувалось раніше, такі цілеспрямовані дії називають керуваннями і позначають п(і).

Характер руху технічної системи визначається системою дифе­ренціальних рівнянь

Хі=8і(х,п,у), Хі(0) = Сі г = 1,...,п, (5.10)

де Сі, / = 1,...,и характеризує початковий стан технічної системи.

Інколи цю систему скорочено записують у векторній формі у вигляді одного диференціального рівняння

І = 8(х,п,У), х(0) = С. (5.11)

Керування п(і) входить у рівняння (5.11), оскільки це рівняння визначає не просто конкретний рух технічної системи, а лише її технічні можливості, які можуть бути реалізованими шляхом вико­ристання того або іншого керування з простору допустимих керу­вань II .

Оцінити, наскільки при тому або іншому способі керування досягаються поставлені цілі, можна, як і раніше, шляхом уведення цільової функції (5.3), яку в даному випадку зручно записати у ви­гляді

У = Уу[х(і)Мі)і (5-12)

Так, якщо и(і) — миттєва витрата палива, а х(і) — миттєва швидкість автомобіля, то з точки зору витрат палива якість керу­вання в будь-який момент часу може бути охарактеризована ве­личиною

у(ґ) = и(і)/х(і), (5.13)

де у{і) - миттєва витрата палива на одиницю шляху.

При цьому необхідно відзначити, що функція у{і) буде зале­жати від некерованих зовнішніх впливів V, тобто сукупності зовнішніх факторів, які визначають умови руху автомобіля.

Цільову функцію (5.13) використовують досить рідко, оскільки вона дає оцінку лише миттєвих значень процесу керування, тоді як у більшості випадків виникає необхідність оцінити процеси в технічних системах протягом усього часу керування від 0 до 1\.

У багатьох випадках цільову функцію вдається підібрати та­ким чином, що оцінку процесу в технічній системі можна здійснити шляхом інтегрування цільової функції за весь час керування, тобто за критерій якості керування прийняти функціонал

175

Цп) = \оУу[х(і),п(ф- (5.14)

Так, якщо цільова функція має фізичну суть витрат, то вираз (5.14) визначає сумарні витрати за весь процес керування.

Інколи мета керування є бажаним ходом процесу 2(і). При цьому за цільову функцію можна взяти квадрат або абсолютне значення відхилення дійсного процесу х(і) від бажаного:

у(і) = [х(і)-г(і)]²; у(і) = \х(і)-ї(і)\. (5.15)

У цих випадках критерій якості керування (5.15) буде визначати повну квадратичну або абсолютну похибку.

У динамічних задачах керування поряд із обмеженнями І/ ={«!,...,м#}, які визначають простір допустимих керувань п, доводиться мати справу з інтегральними обмеженнями вигляду

ід' ^_V[X(І), п(І)]СІІ < 1_т= СОП8І. (5.16)

Досить часто доводиться мати справу з обмеженнями меж зміни миттєвого значення деякого параметра а (х~, п) в процесі ке­рування. Позначимо через а§ таке значення параметра а, переви­щення якого є небажаним. Якщо підінтегральну функцію ()у(х~,п),

яка має назву в даному випадку Функції штрафу, визначити із співвідношення

^О^Нг,.^ „12 ⁽⁵¹⁷⁾

[0, а<а₀;

[[а(х,п)-а₀]² ,а>а₀, то інтегральне обмеження (5.16) буде визначати вимогу, щоб миттєве значення параметра а могло перевищувати а о лише корот­кочасно і на незначну величину. Ця умова буде виконуватися тим жорсткіше, чим менше І_т. Так, при 1^=0 обмеження (5.16) узагалі не буде допускати перевищення а над а$.

Обмеження виду (5.16) виникають також тоді, коли необхідно мати справу з обмеженими ресурсами (енергії, палива і т. п.).

На основі наведених співвідношень можна дати таке виз­начення оптимального керування в динамічних системах.

Оптимальним називається керування п (і), яке вибирається з простору допустимих керувань II, таке, яке для системи, що опи-

176

сується диференціальним рівнянням (5.11), мінімізує критерій якості (5.14) при заданих обмеженнях на ресурси (5.16), котрі використо­вуються в процесі керування.

Динамічні задачі керування, як і однокрокові, можуть бути де­термінованими, якщо простір стану некерованих впливів V складається тільки з одного елемента Уд, і стохастичними. якщо простір станів некеро­ваних впливів V складається більш ніж з одного елемента і заданий апрі­орний розподіл імовірностей р (V ) на просторі V .

Серед стохастичних задач важливе місце займають задачі адаптивного керування, які використовують у тих випадках, коли апріорних даних про стан некерованих впливів недостатньо для здійснення ефективного керування або коли відсутній достатньо точний опис самої технічної системи. Адаптивне керування має за мету уточнення даних про стан навколишнього середовища або вла­стивості технічної системи безпосередньо в процесі керування шля­хом випробовування різних способів керування і пошуку того з них, який у тих чи інших конкретних умовах виявляється найбільш ефек­тивним.

5.3.3. Керування кінцевим станом

У ряді випадків характер руху технічної системи в процесі ке­рування не викликає суттєвого інтересу, а важливим є тільки стан, який прийме технічна система в момент закінчення процесу керу­вання. Прикладами подібних задач може бути доставка вантажу до заданого строку в заданий пункт призначення, досягнення технічною системою до визначеного терміну заданої продуктивності і т. п. Такі задачі називають задачами керування кінцевим станом.

Позначимо через х(і{) стан технічної системи в кінцевий мо­мент часу 11. Тоді цільова функція має вигляд

У = уЛ*(іі)і (5-18)

Оскільки х(і{) залежить від характеру застосованого керування и(і), то і значення у також буде залежати від застосованого керу­вання. Тому задачу вибору оптимального керування можна сформу­лювати для цього випадку наступним чином: із простору допусти­мих керувань II вибрати таке керування м (і), яке для технічної системи, що описується диференціальним рівняннями (5.11),

177

мінімізує цільову функцію (5.18) при обмеженнях (5.16) на ресурси що використовуються в процесі керування.

5.4. Оптимальне керування як варіаційна задача

5.4.1. Математичне формулювання задачі оптимального керування

Характерною тенденцією в побудові сучасних технічних сис­тем є прагнення отримувати системи, які з певних позицій можна вважати найкращими. При керуванні технічними системами, що ви­конують технологічні процеси, ці прагнення виражаються в тому, щоб отримати максимальну кількість продукції високої якості при обмеженому використанні ресурсів (сировини, енергії тощо). При керуванні транспортними технічними системами прагнуть мінімізувати час транспортування, кількість витраченого палива і т. п. У системах стабілізації викликає інтерес досягнення максимальної точності при наявності різних обмежень, що накладаються на коор­динати технічної системи.

В усіх цих прикладах задачі керування зводяться до знахо­дження найкращого з певних позицій процесу з множини можливих процесів, тобто вони належать до класу динамічних задач опти­мального керування.

Як було показано раніше, математичне формулювання ди­намічних задач оптимального керування зводиться до наступного. Існує технічна система як об'єкт керування, стан котрої характери­зується миттєвою змінною х =(х],...,х_п). Характер процесів у технічній системі можна змінювати, використовуючи те або інше ке­рування и з простору допустимих керувань І/. В загальному випадку керування и є V може бути також миттєвою ве-личиноюм =(иі,...,ик).

Характер руху технічної системи описується системою дифе­ренціальних рівнянь

х = /(х,и),х(0) = с. (5.19)

За критерій якості керування приймають інтегральний функціонал виду

іо(и) = )/_о[х(і)м(Ф. (5-20)

о

178

який фізично являє собою витрати. Тут /] - час проходження проце­су керування; /о[х(і),и(і)] = Уо(і) - миттєві витрати в момент і при стані системи х(і) і керуванні и(і).

Допоміжними можуть бути обмеження, що накладаються на кількість ресурсів або межі зміни деяких параметрів, які виз­начаються математичним співвідношенням

ц

\д[х(ї),и(і)}і( = І_т. (5.21)

о

Як було встановлено раніше, оптимальним називають таке ке­рування и з множини допустимих керувань V, при якому для систе­ми, що описується диференціальним рівнянням (5.19), при заданих обмеженнях на існуючі ресурси (5.21) критерій якості керування (5.20) приймає мінімальне (максимальне) значення.

Сформульована подібним чином задача оптимального керу­вання відноситься до класу варіаційних задач, розв'язуванням яких займається розділ математики, який отримав назву варіаційного числення. Величина ](и), що визначається співвідношенням (5.20),

називається функціоналом. На відміну від функції, наприклад /(х), числові значення якої задаються на множині значень аргумента X, числові значення функціонала Іо(и) задаються на множині всяких керувань и{і).

Завжди задачі, що вимагають мінімізації функціонала (5.20), при наявності інтегрального обмеження (5.21) замінюються мінімізацією нового функціонала

\(и) = \іь(хм)(1і + Ц0(хц)аі, (5.22)

о о

який підпорядкований тільки диференціальному співвідношенню (5.19). Параметр Я у функціоналі (5.22), що отримав назву множни­ка Лагранжа, в задачах оптимального керування відіграє роль "ціни" обмежених ресурсів. Його значення знаходиться із граничних • умов варіаційної задачі.

Застосування методів варіаційного числення до задач знахо­дження оптимального керування не одержало поширення в зв'язку з цілим рядом труднощів, які виникають при цьому. Тому не будемо спинятися на методах розв'язування варіаційної задачі, а зацікавлених цим питанням відсилаємо до [30]. Відзначимо лише де­які моменти, які важливі для подальшого викладання матеріалу.

179

Найважливішим поняттям варіаційного числення є поняття варіації функції, яке при дослідженні функціоналів відіграє таку ж роль, як диференціал при дослідженні функцій.

Нехай /(х) — функція, неперервна на інтервалі [а, Ь]. Розгля­немо внутрішню точку х цього інтервалу і деяке фіксоване значення диференціала аргументу функції Ах = йх. Тоді різницю значень функції в точках х + Ах та х

Дх + АХ)- Дх) = йДх) = /'(X) АХ (5.23) називають диференціалом функції /(х) у точці X. Умова <і/(х) =0 є необхідною умовою мінімуму функції/(х) у точці х.

Для отримання аналогії з варіаційним численням зручно дифе­ренціал (ї/(х) визначити по-іншому. Розглянемо значення функції /(х + є Ах). При фіксованих х та Дх воно буде функцією від £. Диференціюючи цю функцію за Є і вважаючи £= 0, отримаємо

— Дх + є Ах) | _£=0 = /\х)Ах = (іДх). (5.24)

Розглянемо аналогічні поняття варіаційного числення. Нехай и(і) і и\(() —дві функції керування системою. Різницю

Ьи(і) = щ(і)-и(і) (5.25)

називають варіацією функції и(і), а різницю

61(и) = 1(и + ди)-Хи) (5.26)

називають варіацією функціонала.

Варіацію функціонала можна визначити по-іншому. Для цього розглянемо при фіксованих и(() та 8и(і) функціонал

і(и + гЬи) = ц(і), (5.27)

який є функцією £. Припустимо, що функціонал (5.27) визначений для різних £. Це означає, що можливі різні керування и(і) + є8и(і) поблизу фіксованого керування и(і), тобто и(і) являє собою внутрішню точку простору допустимих керувань II. При цьому варіацію функціонала можна визначити за аналогією з дифе­ренціалом функції, який визначено співвідношенням (5.24). В ре­зультаті цього отримаємо

Щи) = ~Ци + гМ\^. (5.28)

оє

180

Якщо и(і) становить оптимальне керування, то функція <р(є) буде досягати мінімуму при е= 0. У цьому випадку

^дФ)\_£=о =^-Хи + єАи)_їг=0 = 0, (5.29)

дг ^Е=" де

тобто Щи) = 0. Таким чином, оптимальним керуванням буде таке, при якому варіація функціонала дорівнює нулю.

У варіаційному численні умова 5і(и) використовується для отримання диференціального рівняння Ейлера [30], серед множини розв'язків якого і визначається керування и(і), що мінімізує функціонал (5.22).

5.4.2. Проблеми розв'язування варіаційної задачі

При знаходженні оптимального керування варіаційними мето­дами доводиться мати справу з труднощами, які мають принципо­вий характер:

1. Варіаційні методи дають можливість знаходити тільки відносні максимуми функціонала X^й) > ^Т°ДЇ ^як інтерес викликає зна­ ходження абсолютного максимуму або мінімуму.

2. Рівняння Ейлера для багатьох технічних систем виявляються нелінійними, що часто не дає можливості отримати розв'язок варіаційної задачі в явному вигляді.

3. Часто оптимальне керування технічними системами має розриви. Метод множників Лагранжа не в змозі визначити кількість та місце розташування точок розриву, і тому в цих випадках він не дає можливості знайти оптимальне керування.

4. На значення керуючих впливів і фазових координат технічних систем досить часто вводяться обмеження у вигляді нерівностей, що не дає можливості знаходити оптимальне керування варіаційними методами.

Оскільки остання обставина мала вирішальне значення для роз­витку нових ідей в області оптимального керування, то спинимося на ній більш детально.

Звичайними обмеженнями, що накладаються на сигнали керу­вання, є обмеження виду

\ц_х(і)\<>М_і% (5.30)

які означають необхідність обмеження за величиною сигналів керу­вання. Так, обмеженими можуть бути: напруга, яка підводиться до якоря електродвигуна, граничний кут повороту руля автомобіля,

181

гранична температура в камері згоряння двигуна внутрішнього зго­ряння і т. п. При цьому отримання оптимальних процесів вимагає, як правило, підтримання сигналів керування на граничних значеннях, що відповідає найбільш швидкому й ефективному про­ходженню процесів у технічній системі. Типовий для цих випадків характер зміни керування и(і) при оптимальному процесі наведено на рис. 5.1.

-М

Рис. 5.1. Характер­ний вигляд опти­мального сигналу керування техні­чною системою

Однак граничні значення керування и(і) лежать на межах області до­пустимих керувань V і, природно, не є внутрішніми точками цієї об­ласті, для яких тільки справедливі варіаційні методи. Правда, обме­жень виду (5.30) можна позбутися шляхом уведення нових змінних V/, які зв'язані зі змінними м, співвідношенням м_г= М/ зіпУ_г-. При цьому значення |м_г-|= —Мі будуть відповідати змінним У;=+7г/2, що є

внутрішніми точками області нових допустимих керувань. Однак така заміна змінних, як правило, приводить до значного ускладнення отри­маних рівнянь.

Наведеш труднощі сприяли інтенсивному вивченню проблеми оптимальності керування технічними системами. Л.С.Понтрягін і його учні, В.Г.Болтянський, Р.В.Гамкрелідзе та Є.Ф.Міщенко створили те­орію оптимального керування [31], в основі якої лежить сформульова­ний Л.С.Понтрягіним принцип максимуму як необхідна умова екстре­муму функціонала при різних обмеженнях і умовах. Цей принцип дав змогу побудувати теорію оптимального керування на строгій матема­тичній основі й відкрив широкі можливості для її практичного застосу­вання при керуванні технічними системами.

182

5.5. Принцип максимуму Понтрягіна 5.5.1. Формулювання принципу максимуму

Мета керування в задачі оптимального керування полягає в мінімізації деякого функціонала. Розглянемо задачу з функціоналом

Н

І = \Л{х(і)м(і),і)іі + Ф{х(і₁)їх), (5.31)

о який являє собою суму інтегрального функціонала

<1

\/§[х(і),и{і),ї)сіі і термінального функціонала Ф(х(і_і)^₁). Ця за-

0

дача має назву задачі Больца. її окремими випадками є задача з інтегральним функціоналом (задача Лагранжа) і задача з термінальним функціоналом (задача Майєра). Задача з інтегральним функціоналом при /о = 1 називається задачею опти­мальної швидкодії.

Відзначимо, що при фіксованих І\,х$ і допустимому керуванні и{і) стан технічної системи х(ї) та значення функціонала (5.31) ви­значаються однозначно. Задача оптимального керування полягає в мінімізації цього функціонала на множині наборів (І\,х$, и, х).

Набір (^,Хо, и, х), який мінімізує функціонал (5.31), нази­вається розв'язком задачі оптимального керування, керування и — оптимальним керуванням, а х — оптимальним станом. Часто розв'язком задачі оптимального керування називають пару (и, х).

Розглянемо наступну задачу оптимального керування з функціоналом (5.31)

Чи) = \/ь{х(і)м(і)л}іі -♦ пап, о

х(0 = /(х(і),и(04х(0)є Хо,х(іі)є Х_х, (5.32)

и(і)€ІІ,0<і<і₁.

При цьому вважається, що момент і-у не фіксований, тобто розгля­дається задача з незакріпленим часом; множина V не залежить від часу, а фазові обмеження відсутні. Уведемо функцію

183

п

Н(х,и,(,щ,уг)=% Уі/і(х,и,і), (5.зз)

*=0

де Щ - константа, у/(ї) = (у/і(і),...,у/_п(і)). Функція Я називається функцією Гамільтона. яка відіграє тут роль, аналогічну функції Ла-гранжа у варіаційному численні. Функцію Н називають також функцією Понтрягіна. Функції Лагранжа і Гамільтона (Понтрягіна) мають такий самий вигляд, що й відповідні функції у варіаційних задачах класичного типу, тільки в ці функції не входять обмеження на керування, які в цьому випадку мають вигляд включення и є І/. Відзначимо, що область керування при цьому може мати будь-яку довільну природу. Вона може бути замкненою множиною або скла­датися зі скінченного числа ізольованих точок. Саме в цьому поля­гає принципова різниця між теорією оптимального керування та теорією класичного варіаційного числення, де завжди вважалось, що область зміни функцій керування відкрита і вони є неперервни­ми, а функції /(х,и,ї) і /д(х,и,ґ) неперервно диференційовані. Для розглянутої задачі справедлива теорема 1 [31]. Теорема 1

Нехай вектор-функція и {і) є оптимальним керуванням,

а вектор-функція х (і) — відповідним оптимальним станом у сфор­мульованій задачі оптимального керування. Тоді існує непере­рвна вектор-функція у/ (і) = Ш\(і),...,у/_п({)\ і число у/д — ^ таке, що:

І) вектор-функція виду у/* = (щ(і), У*(0ь 0<(<ііє нульовий;

2)вектор-функція у/ (і) є розв'язком системи дифе­ренціальних рівнянь:

V,- (0 = - ~^Н{х(і)м(і)то МО)

и=и (і)' х=х*(і)

= -¥о ^-ШіШФ)- ЇУ/О^/№Ом(ОЛ (⁵-^з4)

ах_{ у₌₁ дХ(

і = і,2,...,п;

184

век-

3) при кожному І е[0, і і] функція НІх (і),у/ (і),ш шорної змінної и = (ііі,...,и_т) досягає максимуму на множині и = и (і), тобто

НІх* (і), у/* (і), и*(О) = тах#(х*(О, У*(0, Л

^У ' иєї/ ^V ' (5.35)

0<і<і_Ґ,

4) при кожному ґє[О, ^] виконується рівність

н{х*(і),¥*((),и*(і))=О. (5.36)

У формулюванні цієї теореми головною є умова максимуму (5.35). Саме тому теорему й назвали принципом максимуму. Умова 1 теореми виключає випадок Н = 0 і робить рівність (5.35) змістовою. За допомогою функції Гамільтона праву частину рівнянь ста­ну з (5.32) можна записати у вигляді

, , ч дН(х, у/, и,і) . ₁ /і{х,и,() = у' \ і = і,...,п.

Тоді початкову систему рівнянь стану з (5.32) разом з лінійною сис­темою (5.34), яку називають спряженою системою, часто записують у симетричному вигляді:

у_і=-дН{х,у,и,ї)Ідх_і, і = 1,..., л.

Якщо в конкретній задачі вдається показати, що у/₀ Ф 0, то завжди можна прийняти щ = -1, оскільки рівності (5.34) - (5.36) не змінюються при множенні їх на довільне число. Можливий випадок також, коли і//0 = 0. Тоді функція Гамільтона не включає /₀, а це оз­начає, що необхідні умови теореми 1 не включають інформації про функціонал І(м). Замінюючи початковий функціонал іншим, отри­маємо для нової задачі ті ж самі умови оптимальності у формі прин­ципу максимуму, що і для початкової. Задачі оптимального керу­вання подібного типу називають особливими (або виродженими).

Рівність (5.36) використовується в основному для ви­значення кінцевого моменту часу і у і включена в число необхідних умов оптимальності тому, що тут розглядається задача

185

з нефіксованим часом керування. Якщо функції и (І) і Ці (І) задо­вольняють рівності (5.34), (5.35), то Нїх (і), у/ (і), и (і), і) = соіщ,

і тому при розв'язуванні конкретної задачі рівність (5.36) достатньо перевірити тільки для одного довільного фіксованого моменту

.Теорема 1 про принцип максимуму не дає повної відповіді на питання, як знайти оптимальне керування, оскільки про вектор уг(і) нам відомо тільки те, що це певний розв'язок системи (5.37), але невідомо, який саме. Однак принцип максимуму дає інформацію про структуру оптимального керування, що полегшує розв'язок за­дачі.

Принцип максимуму дає тільки необхідні умови оптималь-ності. Тому якщо певне допустиме керування задовольняє цьому

принципу, то воно не обов'язково є оптимальним. Функцію и (і), яка задовольняє всі умови теореми 1, називають екстремаллю Понт-рягіна. Лише для деяких класів задач (наприклад, лінійних задач оп­тимальної швидкодії) принцип максимуму є як необхідною, так і до­статньою умовою оптимальності.

У прикладних задачах принцип максимуму нерідко дає мож­ливість однозначно визначити оптимальне керування. Так, якщо завчасно відомо, що оптимальне керування існує і, крім того, знайдено єдине допустиме керування, то це єдине керування є опти­мальним.

Наведемо також формулювання принципу максимуму для за­дачі з фіксованим часом керування. Для цього звернемось до задачі оптимального керування, яка відрізняться від попередньої тільки тим, що тут час керування 1\ будемо вважати фіксованим, тобто за­даним із самого початку.

Для цієї задачі справедлива наступна теорема. Теорема 2.

Нехай вектор-функція и (і) являє собою оптимальне ке­рування, а х (і) — відповідний йому оптимальний стан сис­теми в задачі оптимального керування з фіксованим часом ке­рування її. Тоді існує неперервна вектор-функція

у/ (і) = Ші(і),...,у/_п(і)\ і число У'О-О такі, що виконуються умовиі), ...,3) теореми 1.

186

Єдине, чим відрізняються умови оптимальності теореми 2 від умов оптимальності теореми 1, полягає у відсутності рівності (5.36). У розглянутій задачі час /] задано, тому стає зайвою умова для його визначення.

5.5.2. Про методи розв'язування задач оптимального ке­рування

Спинимось на схемі застосування принципу максимуму. Розг­лянемо задачу оптимального керування з фіксованим часом керу­вання. Знаходження екстремалі Понтрягіна починається з централь­ної умови принципу максимуму

Н(х,\[/,и)^>тах, иеіі, (5.38)

з якої при кожному фіксованому наборі х, у визначають керування и, що є функцією параметрів хі у/, тобто

и = и{х,у). (5.39)

У загальному випадку це зробити досить складно, однак для деяких класів задач керування функцією (5.39) вдається записати в явному вигляді.

Нехай, наприклад,

т /і(х,и) = /_і(х)+'£/_ік(х)и_к, і = 0Д...,л,

V

= [иеК^т], а_к<и_к<Ь_к, А: = 1,2,...,

т,

де а_к,Ь_к - задані числа. В цьому випадку функція Гамільтона має вигляд

т

я=XV,-/;■(*)+х

и_к

к=\

ЇУі/ікі*)

г=0

./=о

і досягає максимуму (завдяки лінійності по м) тільки в граничних точках множини V, а саме при

п

ь_к, якщо 2>і//*(*) >о;

і=0

и_к=\

а_к, якщо ^у/і/_ік(х)<0. і=0

187

Припустимо, що функція (5.39) знайдена. Підставимо ц в початкову і спряжену їй системи. В результаті цього будемо мати

х = /(х, и(х, ц/)\

(5 40) у = -дН(х,у/,и(х,\і/))/дх, 0<і<і_ь

де

дН/дх = (дН/дх_х, дН/дх₂,..., дН/дх_п). Отримано систему 2л диференціальних рівнянь відносно невідомих функцій Хі,Х2,---,х_п,Щ,у/2,---,у/_п, загальний розв'язок якої містить 2л довільних постійних. Після знаходження загального розв'язку ці довільні постійні визначають із 2и крайових умов:

х(0) = Х⁽°\х({₁) = Х⁽¹⁾. (5.41)

У результаті використання умов (5.41) одержують деякі функції х(і) і X}/ (і). Для визначення у/о достатньо, як відмічалось раніше, розг­лянути два випадки, у/$= 0 і у^д = -1, і встановити, який із них має місце в дійсності. При цьому необхідно враховувати, що вектор-функція (у^о,у/(і)) повинна бути ненульовою.

Нехай функції х(і) і у/(і) знайдені. Тоді, підставивши їх у (5.39), отримаємо

и = и(х(і),щ(і)), 0<і<і_ь

Припустимо, що функція й виявилась кусково-неперервною, причому й= -и(х(ґ),цУ(і))€ІІ при кожному *є[0,/і]. Тоді ця

функція є екстремаллю Понтрягіна, а це значить, що вона входить у число керувань, які можуть бути оптимальними. Якщо відомо, що розв'язок задачі оптимального керування існує, і доведено, що екст­ремаль Понтрягіна й єдина, то вона є оптимальним керуванням.

Таким чином, застосування принципу максимуму зводиться до задачі використання умов максимуму (5.38) і розв'язування системи диференціальних рівнянь (5.40) з крайовими умовами (5.41). Це крайова задача принципу максимуму. В тих випадках, коли ЇЇ аналітично розв'язати не вдається, то використовують різні чисельні методи [32].

188

5.5.3. Використання принципу максимуму для оптимального керування механічними системами

Використання принципу максимуму для оптимального керу­вання механічними системами розглянемо на конкретних прикладах.

Приклад 5.1. Розглянемо горизонтальне переміщення краново­го візка з жорстким підвісом вантажу (рис. 5.2).

Нехай у початковий момент часу ( = 0 візок, який ми ототож­нюємо з матеріальною точкою, знаходиться в положенні х = 0 і має швидкість V = 0. Задача полягає в тому, щоб вибрати такий режим роботи приводного механізму, при якому візок перемістився б у по­ложення х = Дл: і при цьому його швидкість була рівною нулеві.

Очевидно, значення сили Р(і) не може бути скільки завгодно вели­ким. Воно обмежене технічними можливостями приводного ме­ханізму, тобто

-Р_г<Р(і)<Р_р, І Є [а/і], (5.43)

де Рр, Р_г - максимально допустимі рушійне і гальмівне зусилля

ПрИВОДу, ЯКІ Є ВеЛИЧИНаМИ ПОСТІЙНИМИ (Рп⁼ СОП8І, Р_г= СОП8І); І\ -

тривалість руху візка.

_{Ч^-гігЧ^}

і	Т
- л *

При цих умовах можливі декілька різних режимів роботи приводного ме- І. ханізму, які забезпечать необхідне пе­ реміщення візка. Необхідно вибрати такий режим руху візка, який із певної точки зору є найбільш вигідним. Вибе­ ремо за критерій такої вигоди мінімум тривалості руху візка, яка забезпечує максимальну продуктивність краново­ го механізму. Інтегральний функціонал Рис. 5.2. Схема горизон- ^такого критерію має вигляд тального руху кранового 'і

візка з жорстким підвісом І = [ (І І —> тІП. (5.44)

вантажу 0

Тепер можна математично сформулювати задачу оптимально­го керування переміщенням кранового візка: знайти кусково-неперервну функцію Р(і), підпорядковану нерівностям (5.43), при

189

якій розв'язок х(і) рівняння (5.42) задовольняє при і= 0 задані початкові умови

х(0) = 0, х(0) = 0,

а при деякому і=і\ — умови в

х(і{) = Ах, х(і_{) = 0,

причому такий, що функціонал (5.44) приймає мінімально можливе значення на множині таких функцій Е. При цьому вважаємо, що клас кусково-неперервних функцій є найбільш широким класом технічно реалізованих функцій Р(і) ■

Сформульована задача є простою задачею оптимального ке­рування. Керуванням у цій задачі служить функція Р{і).

Уведемо такі позначення: х = х_ьх = х₂, Р{і) = и(і), Г_р=а, Г_Т=Ь, Р₀=с, т_п = т.

Після цього задачу оптимального керування рухом візка за­пишемо в такому вигляді: знайти кусково-неперервну функцію и(і),

що задовольняє нерівності -Ь<и(і)<а, 0<і<іі, для якої

розв'язок х (х\((), *2(0)

системи

х₂=(и(()-с)/т Н

задовольняє крайові умови |

хх (0) = 0, *! (іі) = Ах, х₂ (0) = 0, х₂ 00 = 0, (5.46)

причому функціонал

Ци) = І<і{ = і₁ (5.47)

0 досягає свого найменшого значення.

Складемо функцію Гамільтона (Понтрягіна) для цієї задачі

Я = у/₀ + ЩХ₂+ У2 («(0-^с)/^т- (⁵-⁴⁸)

Використавши для цієї функції спряжену систему (5.34), отримаємо

щ=-Н'_Хі=0, іі,₂=-Н'_Х2=-щ.

190

Загальний розв'язок цієї системи має вигляд

Щ(і) = с_ь У₂(і) = -с₁і + с₂,

де С\, с₂ - постійні інтегрування.

Функція Н (5.48) лінійна по відношенню до и, тому умова мак­симуму (5.35) для неї виконується тільки при

„•(₀ = Ь ^¥к'^)>0' [ь, у₂(<)<о.

Таким чином, оптимальне керування и (і) може приймати

# лише два значення а і - Ь і має, виходячи з лінійності функції у/₂ > ^не

більше від одного перемикання, тобто такої точки, в якій функція

*

и (і) змінює свій знак. Тоді оптимальне керування має вигляд

• \ а, 0<Кі₂, и (0 = 1 , (5-49)

\-Ь, І₂<і<і_ь

де ?2 ■ момент перемикання керування.

За допомогою системи рівнянь (5.45) при керуванні (5.49) знайдемо оптимальний за швидкодією режим руху кранового візка:

[ [(а-с)/т]/²/2 + с₁/ + с₃, 0<?</₂,

{- [{Ь + с)/т]і²/2 + с₂і + с₄, І₂< 1<1_{Ь (5 5())}

_х (,) = { К^Д-^С)Н^{Г + С}1' °^^і<{2, \-[(Ь + с)/т]і + с₂, І₂<г<,і_ь

де с і, с2, с з, с 4 - постійні інтегрування.

Із крайових умов руху візка знаходимо постійні інтегрування: с₁₌с₃=0;

с₂=[{Ь + с)/т]і_Ґ, (5.51)

с₄=Ах-[(Ь + с)/т]іі/2.

191

З умов неперервності швидкості х та переміщення х краново­го візка знайдемо моменти часу перемикання рушійної сили 1^ і мінімальної тривалості руху (\:

П=,2

(5.52)

(а + Ь)Ах (а + с)(Ь + с)' '¹ а + Ь

* Рис. 5.3. Графіки зміни пе­реміщення х, швидкості х і прискорення х візка при оптимальному за швидкоді­єю режимі руху при обме­женнях на діючі сили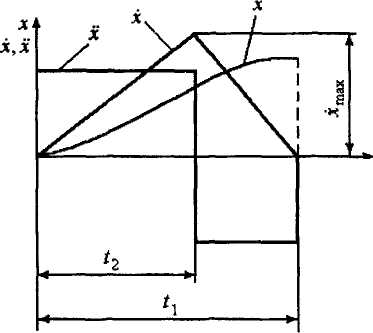

Оптимальним за швидкодією при обмеженнях рушійної і гальмівної сили приводу є режим руху кранового візка, який скла­дається з ділянок рівноприскореного руху й рівносповільненого га­льмування (рис. 5.3).

Однак при цьому режимі руху зростає максимальна швидкість візка *_тах, що приводить до значного збільшення енергетичних витрат.

Приклад 5.2. Розглянемо ускладнену задачу з прикладу 5.1, у якій, крім обмежень на рушійну і гальмівну силу, вводяться обме­ження на енергетичні витрати у вигляді інтегрального функціонала

1 П ?

І_т= — \-т„х <іі<А, (5.53)

'і О²

де А - допустима величина енергетичних витрат у процесі руху кра­нового візка. У виразі (5.53) враховані тільки енергетичні витрати, які йдуть на подолання інерційних сил опору. Енергетичні витрати,

192

що йдуть на подолання статичної складової сили опору пе­реміщенню візка, не враховані в нерівності (5.53), оскільки вони не залежать від режиму руху.

Тут використовуються такі ж позначення, як і в попередній за­дачі. Тому задачу оптимального керування рухом кранового візка в розширеній постановці можна сформулювати наступним чином: знайти кусково-неперервну функцію и(і), що задовольняє нерівності

-Ь< и{і)<а, 0 </</], для якої розв'язок х{хі(і),Х2(0) систе­ми (5.45) задовольняє крайові умови (5.46), причому функціонал (5.47) досягає мінімуму при обмеженні на функціонал

1 ^Ч

— \тх\йі<А. (5.54)

2і_і0

Для цієї задачі запишемо функцію Гамільтона

Н = -щтхуіі+щх₂+щ(и(і)-с)/т. (5.55) Із функції (5.55) отримаємо спряжену систему рівнянь:

^о=О; Щ=-Н'х_х=0; У2=-Н'х₂=-Щ—Х2-Щ.

Загальний розв'язок цієї системи має вигляд

т

Щ=сц\ ¥\ = с\; \і/₁ = -щ—х_г-с₁і + с₂,

ч

де с о, с і, с 2 - постійні інтегрування.

Функція (5.55) лінійна по відношенню до и, тому її максимум досягається при крайніх значеннях и. Якщо на деякій ділянці руху візка у^(0 ⁼ СОП8І, то 1/^2 = 0. З останньої рівності випливає, що

*2(0 = - —• (⁵⁵⁶>

с_от

У рівності (5.56) величини Сд, Сі, т, 1\ є сталими, а це значить, що на цій ділянці х₂(() = сопзі, а и (і) — с.

193

Таким чином, для забезпечення оптимального за швидкодією режиму руху кранового візка з обмеженнями на енергетичні витра­ти, рушійну і гальмівну силу приводу функція керування повинна мати такий вигляд

0<і<і₂,

а,

"(0 =

с, Ї₂<і<і₃, -Ь, і₃<і<Ц,

де ?2» ^3 ~ моменти часу для перемикання рушійної сили. Тоді опти­мальний режим руху візка визначається залежностями:

[(а-с)/т]{ + с_и 0<і<і₂;

*2(0 =

^5:

і₂<кіу,

-[(Ь + с)/т]і + с₂, І₃<і<г_х\

[(а-с)/т]і²/2 + Сіі + с₃, 0<і<і₂;

_Хі(і) =

с₅і + с₆,

і₂<і<і₃;

-[(Ь + с)/т]і²/2 + с₂і + с₄, і₃<і<і_ь

де С}, С2,...,Сб - постійні інтегрування, частина яких С\, с₂, с^с^ визначаються з крайових умов руху візка за допомогою системи (5.51), а інша частина с$, с^ і моменти часу і\, 1₂,1 з визначаються з умов непе­рервності швидкості х(і) та переміщення х(() візка й обмеження на енергетичні витрати його переміщення, виходячи з системи рівнянь:

С5=[(а-с)/т]і₂; с₆=-[(Ь + с)/т]іі; і₂=(і_х-і_г){Ь + с)І{а-с);

Ах = [(« - с)(2і₃-1₂)(₂₊ (Ь + _с)(/_г І₃)³]/(2т); ^ = [(_в-с)²(ЗГз-2/₂)гІ+(* + _С)(ї₁-/з)³]/(біп/₁>

194

Оптимальним за швидкодією при обмеженнях рушійної та гальмівної сили і енергетичних витрат приводу є режим руху крано­вого візка, який складається з ділянок рівноприскореного пуску, сталого руху і рівносповільненого гальмування (рис. 5.4).

і

X,			X
х,х	/ /		^г —'—'
			\ <
	ч			і
		'і

Рис. 5.4. Графіки зміни переміщення х, швидкості х і прискорення х кранового візка при оптимальному за швидкодією режимі руху й обмеженнях на діючі сили та енергетичні витрати

195

СПИСОК ЛІТЕРАТУРИ

1. Гермейер Ю.Б. Математическая теория исследования опера- ций.— М.: Наука, 1971.

2. Берталанфи фон Л. Общая теория систем: Критич. обзор // Исследования по общей теории систем.— М., 1969.— С. 5 - 29.

3. Богданов А.А. Теория организации или тектология.— М., 1913.

4. Калман Р., Фал б П., Арбиб М. Очерки по математической теории систем.— М.: Мир, 1971.

5. Философский знциклопедический словарь.— М.: Советская знциклопедия, 1983.

6. Михалевич В.С., Волкович В.Л. Вьгчислительньїе методьі ис­ следования и проектирования сложньїх систем.— М.: Наука, 1982.— 286 с.

7. Бусленко Н.П., Калашников В.В., Коваленко И.Н. Лекции по теории сложньїх систем.—М.: Сов. радио, 1973.

8. Бусленко Н.П. Моделирование сложньїх систем.— М.: Нау­ ка, 1978.

9. Беккер М.Г. Введение в теорию систем "местность- машина".— М.: Машиностроение, 1983.— 311с.

10. Глушков В.М., Иванов В.В., Яненко В.М. Моделирование развивающихся систем.— М.: Наука, 1983.— 337 с.

11. Сівко В.Й. Механічне устаткування підприємств будівельних виробів.— К.: ІСДО, 1994.— 359 с.

12. Яковлев А.С. Советские самолетьі.— М.: Наука, 1975.

13. Венников В.А. Теория подобия и моделирования.— М.: Вьісш. школа, 1976.— 479 с.

14. Брумберг В.А. Аналитические алгоритми небесной меха- ники.— М.: Наука, 1980.— 205 с.

15. Соболь И.М. Метод Монте-Карло.— М.: Наука, 1966.— 87 с.

16. Ловейкин В.С. Расчетьі оптимальних режимов движения механизмов строительнмх машин.— К.: УМК ВО, 1990.— 168 с.

17. Горский Б.Е., Ловейкин В.С. Методика составления опера- торов передачи движения // Горньїе, строительньїе и дорожньїе ма- шиньї.— К.: Техніка, 1979.— Внп. 28.— С. 99 - 105.

18. Самарский А.А. Введение в численньїе методьі: Учебн. посо- бие для вузов.— 2-е изд., перераб. и доп.— М.: Наука, 1987.— 288 с.

19. Растригин Л.А., Маджаров Н.Е. Введение в идентифика- цию обьектов управлення.— М.: Знергия, 1977.— 215 с.

20. Барабанчук В.И. и др. Планирование зксперимента в тех- нике.— К.: Техніка, 1984.— 200 с.

196

21. Корн Г. Исследование сложньїх систем по частям (диакоптика).— М.: Наука, 1972.— 544 с.

22. Назаренко И.Й. Прикладньїе задачи теории вибрационньїх систем.— К.: ИСИО.— 216 с.

23. Чубук Ю.Ф., Назаренко И.И., Гарнец В.Н. Вибрационньїе машиньї для уплотнения бетонньїх смесей.— К.: Вища школа, 1985.— 168 с.

24. Розанов Ю.А. Случайньїе процесові.— М.: Наука, 1979.— 183 с.

25. Молчанов А.А. Моделирование и проектирование слож­ ньїх систем.— К.: Вища школа, 1988.— 317 с.

26. Ризкин И.Х. Машинний анализ и проектирование тех- нических систем.— М.: Наука, 1985.— 160 с.

27. Одрин В.М., Картавов С.С. Морфологический анализ сис­ тем.— К.: Наукова думка, 1977.— 148 с.

28. Основи автоматического управлення / Под ред. В.С. Пу- гачева.— М.: Физматгиз, 1963.

29. Хедли Д. Нелинейное и динамическое программирова- ние.— М.: Мир, 1967.

30. Краснов М.Л., Макаренко Г.И., Киселев А.И. Вариацион- ное исчисление.— М.: Наука, 1973.— 191 с.

31. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищен- ко Е.В. Математическая теория оптимальньк процессов.— М.: Наука, 1976.—392 с.

32. Васильєв Ф.П. Численньїе методьі решения зкстремальньїх задач.— М.: Наука, 1980.

197

ЗМІСТ

Вступ 3 •■