7.1Простые ставки
Из формулы (1) следует (вывод формулы в задаче 20):
(8)
;
(9)
‑ дисконтный
или дисконтирующий множитель, коэффициент
дисконтирования.
Формулу для расчета дисконта получим исходя из условия:
, 
,
итак:
(10)
‑ сумма
дисконта (дисконт).
Вышеприведенные формулы применимы при выражении срока в годах. При выражении интервала начисления в более мелких единицах времени следует поменять в формулах n на t/K, тогда получим:
(8.1)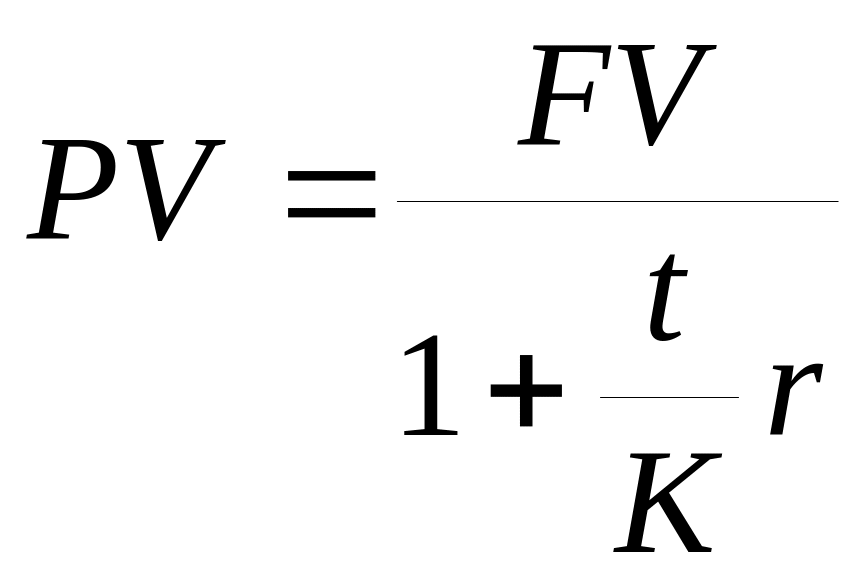
;
(9.1)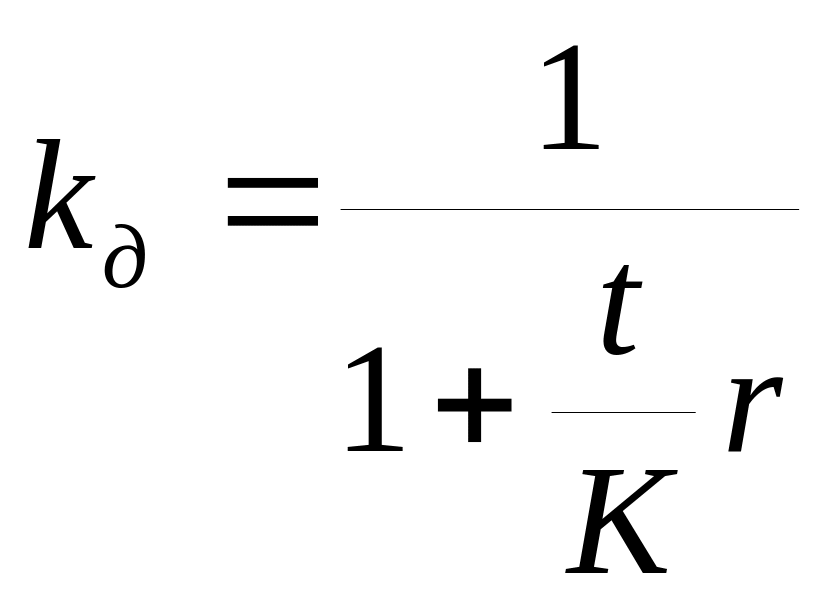
‑ коэффициент
дисконтирования.
(10.1)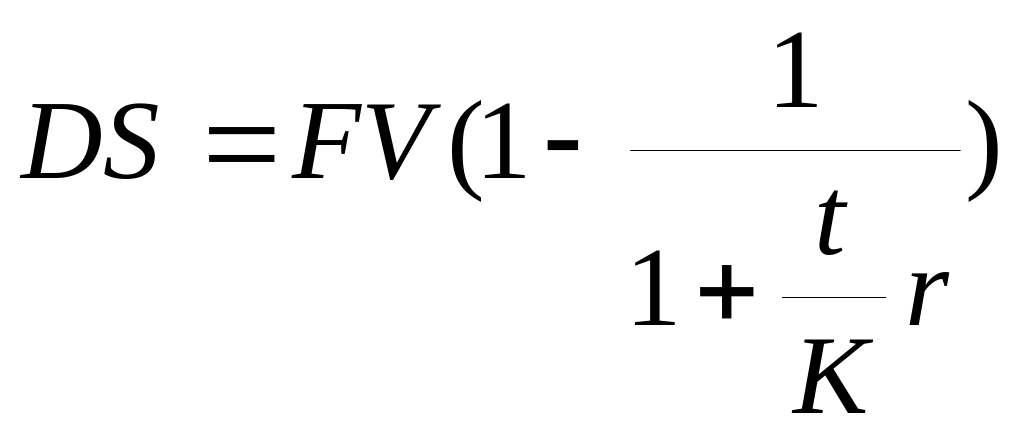
‑ дисконт.
Задача
Какова текущая стоимость денежного поступления в размере 200 тыс. руб. через пять лет, если применяется простая ставка 20% годовых? Рассчитать также коэффициент дисконтирования и сумму процентов.
Решение.
;
;
.
Задача
На какую сумму может быть поставлен товар 1 июня с учетом того, что расчет в сумме 250 тыс. руб. будет произведен 15 сентября, а доходность по коммерческому кредиту предполагается 15% годовых (схема – простые проценты, метод 365/365, год високосный). Определить сумму процентов.
Решение.
Июнь |
30 |
Июль |
31 |
Август |
31 |
Сентябрь |
15-1=14 |
Всего дней: |
106 |
;
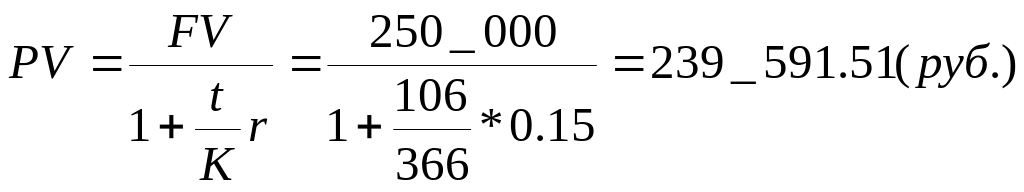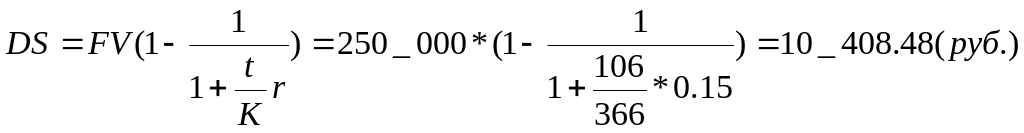
Замечание. Математическое дисконтирование по простым процентным ставкам применяется довольно редко. Дисконтирование вообще наиболее широко применяется для решения двух специфических задач:
учет векселей. В этом случае обычно применяется банковское дисконтирование по простой учетной ставке, а не по ставке наращения, (оно будет рассмотрено позднее);
оценка инвестиций. В этом случае применяется математическое дисконтирование, однако, как правило, не по простой ставке наращения, а по сложной. Последнее вообще характерно для финансовых операций продолжительностью более года.
7.2Сложные ставки
(11)
;
(12)
;
(13)
;
(11.1)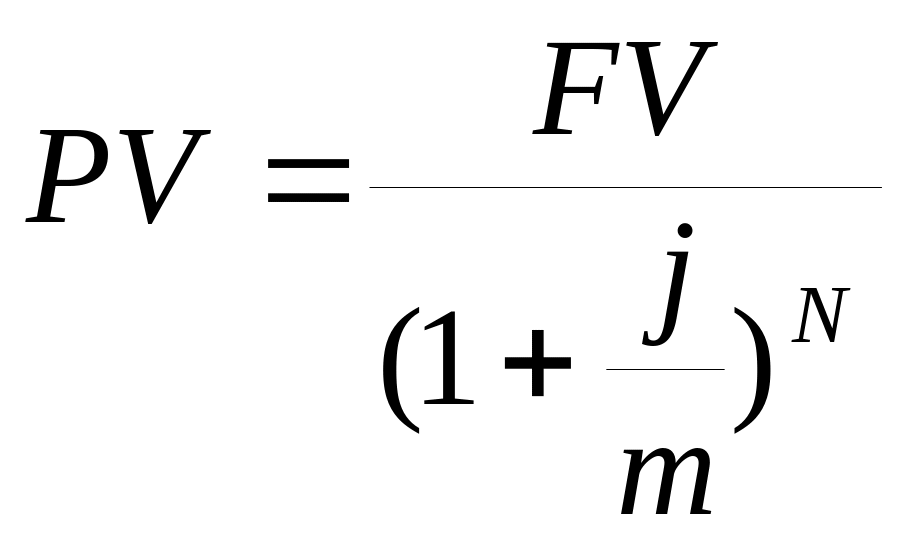
;
(12.1)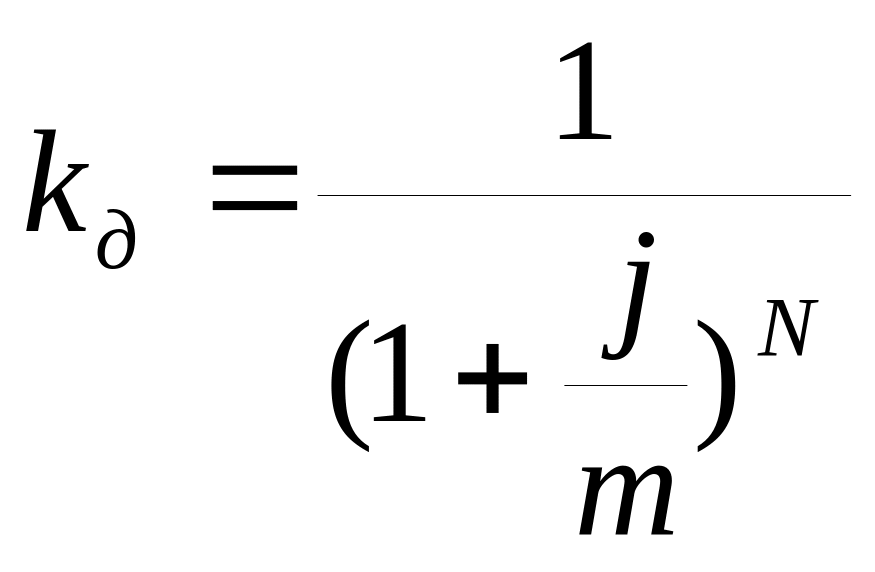
;
(13.1)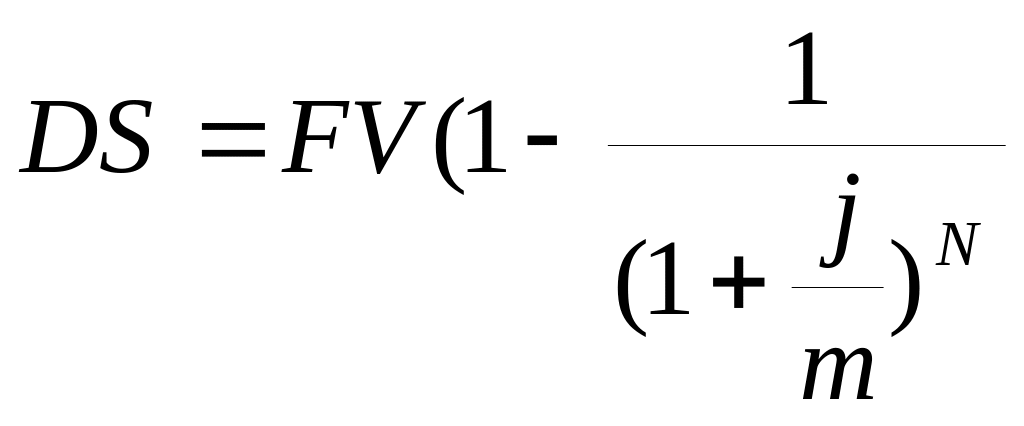
.
Задача
Сумма 5 млн. руб. выплачивается через 5 лет. Необходимо определить ее современную величину при условии, что применяется ставка сложных процентов 12% годовых.
Решение.
Дисконтный множитель для данных условий составит
,
.
Для каких целей необходимо дисконтировать будущие платежи? Примером ответа на этот вопрос является следующая задача.
Задача
Вы хотите вложить свои 100 тыс. руб. в интересующую Вас финансовую операцию, которая через 3 года и 3 месяца закончится и принесет Вам 120 тыс. руб. Оцените целесообразность данного вложения, если у вас есть альтернативная возможность гарантированного размещения средств с ежеквартальным начислением процентов по номинальной ставке 10% годовых.
Решение.
Очевидно, что современная стоимость альтернативного размещения составляет 100 тыс. руб. Найдем современную стоимость дохода, который Вы можете получить по итогам финансовой операции, используя для дисконтирования в качестве ставки сравнения ставку по гарантированному размещению.
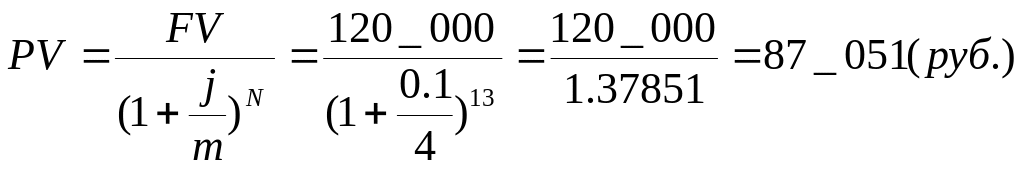
Вывод. Ваши инвестиции в интересный проект убыточны по сравнению с гарантированным использованием средств, поэтому оно не целесообразно.