10. Коло

Властивості радіуса та хорди. Властивості дотичної до кола. Вписані та центральні кути. Вписані та описані многокутники. Довжина кола та дуги. Формули радіусів вписаних та описаних кіл. («Геометрія», с. 13 – 15).

1(1). Радіус кола, описаного навколо трикутника, дорівнює 10 см. Знайдіть сторону трикутника, що лежить навпроти кута 30°.

2(1). В прямокутну трапецію можна вписати коло. Знайдіть площу трапеції, якщо її більша бічна сторона дорівнює 9 см, а висота – 7 см.

3(1). Знайдіть довжину дуги кола, радіус якого дорівнює 9 см, а градусна міра дуги 120°.

4(2). Сторона правильного трикутника, вписаного в коло, дорівнює см. Знайдіть сторону квадрата, вписаного в це коло.

5(3). Радіус кола, вписаного в правильний многокутник, дорівнює см, а радіус кола, описаного навколо нього, – 8 см. Знайдіть кількість сторін многокутника та довжину його сторони.

6(3). Центр кола, описаного навколо трапеції, належить більшій основі. Знайдіть кути трапеції, якщо основи відносяться як 1 : 2.

7(3). Кола, радіуси яких дорівнюють 4 см та 9 см, дотикаються зовнішнім чином. Знайдіть довжину їхньої спільної дотичної.

Завдання для самостійної роботи

8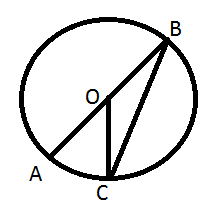 (1). На рисунку О – центр кола, АВС = 40°. Знайдіть кут АОС.

9(1). В чотирикутнику, описаному навколо кола, сума двох протилежних сторін дорівнює 20 см. Знайдіть периметр цього чотирикутника.

10(1). В квадрат зі стороною 14 см вписано коло. Знайдіть його довжину.

11(1). Радіус кола, вписаного в правильний трикутник, дорівнює см. Обчисліть периметр трикутника.

12(3). Навколо рівнобічної трапеції, основи якої дорівнюють 12 см та 16 см, а висота 14 см, описано коло. Знайдіть довжину цього кола.

13(3). Коло, вписане в прямокутну трапецію, поділяє точкою дотику більшу бічну сторону на відрізки 4 см та 25 см. Знайдіть площу трапеції.

Відповіді. 8. 80° 9. 40 см 10. 14π см 11. 36 см 12. 20π см 13. 490 см²

11. Декартові координати та вектори на площині

Центральна симетрія. Відстань між двома точками. Координати середини відрізка. Рівняння кола та прямої. Вектори. («Геометрія», с.15 – 17)

1(1). Знайдіть координати точки, симетричної точці (–5; 2) відносно початку координат.

2(1). Знайдіть координати центра кола (х + 1)² + (у – 2)² = 4.

3(1). Укажіть рівняння прямої, паралельної прямій у = 0,5х – 2.

А) 0,5х + у + 2 = 0 Б) х – 0,5у = 0 В) х – у – 2 = 0 Г) 0,5х – у + 2 = 0

4(1). Скільки розв’язків має система рівнянь

5(3). При якому значенні а точки А(2; 3), В(–3; 5), С(а; 9) будуть лежать на одній прямій?

6(1). Знайдіть координати вектора , якщо .

7(1). Серед векторів оберіть пару колінеарних векторів.

8(3). Знайдіть кут між векторами та , якщо та

9(3). Доведіть, що чотирикутник АВСD є прямокутником, якщо А(3; –1), В(2; 3), С(–2; 2), D(–1; –2).

Завдання для самостійної роботи

10(1). На скільки одиниць треба перемістити точку А(–4) вздовж числової осі, щоб вона перейшла в точку В(7)?

11(1). Вкажіть взаємне розміщення кола х² + у² = 9 та прямої у = –3.

А) не мають спільних точок Б) мають одну спільну точку (–3; 0)

В) мають дві спільні точки (–3; 0) и (0; –3) Г) мають одну спільну точку (0; –3)

12(3). Доведіть, що трикутник KLM з вершинами в точках К(–4; 16), L(6; –4), M(3; –5) прямокутний, та складіть рівняння кола, описаного навколо цього трикутника.

13(1). Знайдіть модуль вектора , якщо М(3; –2), N(–1; –3).

14(2). При яких значеннях m вектори колінеарні?

15(1). Знайдіть косинус кута між векторами

16(3). Доведіть, що АВСD – ромб, якщо А(0; 6), В(5; 7), С(4; 2), D(–1; 1).

Відповіді. 10. 11 11. Г 12. (х – 1)² + (у – 6)² = 125 13. 14. m = 2 15.