Модель Хопфилда
Нейро́нная сеть Хо́пфилда — полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия являются локальными минимумами функционала, называемого энергией сети (рис.20) .
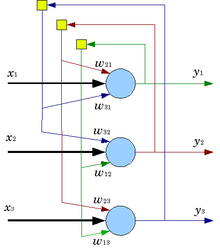
Рис.20. Схема сети Хопфилда с тремя нейронами
Нейронная сеть Хопфилда состоит из
искусственных
нейронов. Каждый нейрон
системы может принимать одно из двух
состояний (что аналогично выходу нейрона
с пороговой функцией активации):
Из-за их биполярной природы нейроны сети Хопфилда иногда называют спинами.
Взаимодействие спинов сети описывается выражением:
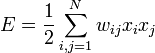
где
—
элемент матрицы взаимодействий
,
которая состоит из весовых коэффициентов
связей между нейронами. В эту матрицу
в процессе обучения записывается М
«образов» — N-мерных бинарных векторов:
В сети Хопфилда матрица связей является
симметричной (
),
а диагональные элементы матрицы
полагаются равными нулю (
),
что исключает эффект воздействия нейрона
на самого себя и является необходимым
для сети Хопфилда, но не достаточным
условием, устойчивости в процессе работы
сети.
Алгоритм обучения сети Хопфилда
существенно отличается от таких
классических алгоритмов обучения
перцептронов,
как метод
коррекции ошибки или метод
обратного распространения ошибки.
Отличие заключается в том, что вместо
последовательного приближения к нужному
состоянию с вычислением ошибок, все
коэффициенты матрицы рассчитываются
по одной формуле, за один цикл, после
чего сеть сразу готова к работе. Вычисление
коэффициентов основано на следующем
правиле: для всех запомненных образов
матрица
связи должна удовлетворять уравнению
поскольку именно при этом условии состояния сети будут устойчивы — попав в такое состояние, сеть в нём и останется.
Модель сети с обратным распространением
Способом обратного распространения (backpropogation) называется способ обучения многослойных нейросетей. В таких нейронных сетях связи между собой имеют только соседние слои, при этом каждый нейрон предыдущего слоя связан со всеми нейронами последующего слоя.
Нейроны обычно имеют сигмоидальную функцию возбуждения. Первый слой нейронов называется входным и содержит число нейронов соответствующее распознаваемому образу. Последний слой нейронов называется выходным и содержит столько нейронов, сколько классов образов распознается. Между входным и выходным слоями располагается один или более скрытых (теневых) слоев. Определение числа скрытых слоев и числа нейронов в каждом слое для конкретной задачи является неформальной задачей. Принцип обучения такой нейронной сети базируется на вычислении отклонений значений сигналов на выходных процессорных элементах от эталонных и обратном «прогоне» этих отклонений до породивших их элементов с целью коррекции ошибки. Еще в 1974 году Поль Дж.Вербос изобрел значительно более эффективную процедуру для вычисления величины, называемой производной ошибки по весу, когда работал над своей докторской диссертацией в Гарвардском университете. Процедура, известная теперь как алгоритм обратного распространения, стала одним из наиболее важных инструментов в обучении нейронных сетей.
Однако этому алгоритму свойственны и недостатки, главный из которых – отсутствие сколько-нибудь приемлемых оценок времени обучения. Понимание, что сеть в конце концов обучится, мало утешает, если на это могут уйти годы.
Приобретение знаний