- •Самостоятельная работа студента с преподавателем №1 (1, 2 недели обучения). Исследование разомкнутой линейной системы Модели линейных систем
- •Коэффициент усиления в установившемся режиме
- •Импульсная характеристика
- •Переходная характеристика
- •Частотная характеристика
- •Полюса и нули
- •Исследование разомкнутой линейной системы Цели работы
- •Задачи работы
- •Оформление отчета
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета по срсп. Исследование разомкнутой линейной системы
- •Описание системы
- •Результаты исследования
- •Самостоятельная работа студента с преподавателем №1 (3, 4 недели обучения). Проектирование регулятора для линейной системы Модели соединений систем
- •Корневой годограф
- •Синтез с помощью лафчх
- •Точность в установившемся режиме
- •Простейшие типы регуляторов
- •Проектирование регулятора для линейной системы Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета по срсп. Проектирование регулятора для линейной системы
- •Описание системы
- •2.Исследование разомкнутой системы
- •4.1 Регулятор, обеспечивающий перерегулирование 10%
- •4.2 Регулятор, обеспечивающий кратчайший переходный процесс
- •Самостоятельная работа студента с преподавателем № 3 (5, 6 недели обучения) Моделирование систем управления в пакете Simulink Создание моделей в Simulink
- •Основные источники сигналов (Sources)
- •Основные устройства вывода (Sinks)
- •Линейные системы (Continuous)
- •Другие часто используемые блоки
- •Блок Scope
- •Оформление графиков
- •Компенсация постоянных возмущений
- •Моделирование систем управления в пакете Simulink Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета. Моделирование систем управления в пакете Simulink
- •1.Описание системы
- •Исследование системы с пд-регулятором
- •3.Исследование системы с пид-регулятором
- •Самостоятельная работа студента с преподавателем № 4 (7, 8 недели обучения) Моделирование нелинейных систем управления Модели нелинейных звеньев (Discontinuities)
- •Подсистемы
- •Б лок Scope (несколько сигналов)
- •Скрипты
- •Форматирование графика
- •Лабораторная работа № 4 Моделирование нелинейных систем управления Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета. Моделирование нелинейных систем управления
- •1.Описание системы
- •2.Построение нелинейной модели
- •3.Сравнение линейной и нелинейной моделей
- •Самостоятельная работа студентов с преподавателем № 5 (9, 10 недели обучения) Программирование в среде Matlab Передача данных в модель Simulink
- •Функции Matlab
- •Некоторые стандартные функции Matlab
- •Программирование в среде Matlab Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета. Программирование в среде Matlab
- •1.Описание системы
- •Самостоятельная работа студента с преподавателем № 6 (11, 12). Оптимизация нелинейных систем Эффект насыщения
- •Компенсация эффекта насыщения (anti-windup)
- •Пакет ncd Blockset
- •Оптимизация нелинейных систем Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета. Оптимизация нелинейных систем в среде Matlab
- •1.Описание системы
- •2.Блок компенсации насыщения
- •3.Оптимальный выбор
- •Оптимизация нелинейных систем Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета. Оптимизация нелинейных систем в среде Matlab
- •1.Описание системы
- •2.Блок компенсации насыщения
- •3.Оптимальный выбор
- •Самостоятельная работа студента с преподавателем №7 (13, 14, 15 недели) Переоборудование непрерывного регулятора Задача переоборудования
- •Компьютер в контуре управления
- •Экстраполятор
- •Фиксатор нулевого порядка
- •Цифровые фильтры
- •Методы численного интегрирования
- •Переоборудование пид-регулятора
- •Алгебраические циклы
- •Цифровая реализация непрерывного регулятора Цели работы
- •Задачи работы
- •Оформление отчета
- •Описание системы
- •Инструкция по выполнению работы
- •Контрольные вопросы к защите
- •Пример оформления отчета. Цифровая реализация непрерывного регулятора
- •1.Описание системы
- •2.Переоборудование непрерывного регулятора
- •3.Подсистема «Регулятор» в цифровой системе
- •4.Выбор интервала квантования
Исследование системы с пропорционально-дифференциальным (ПД-) регулятором
Общий вид передаточной функции регулятора
 ,
где
сек,
сек,
,
где
сек,
сек,
а коэффициент
 должен быть выбран в процессе проектирования
в соответствии с требованиями к системе.
должен быть выбран в процессе проектирования
в соответствии с требованиями к системе.
4.1 Регулятор, обеспечивающий перерегулирование 10%
Для обеспечения перерегулирования 10% требуется выбрать

Переходная функция скорректированной замкнутой системы

Время переходного процесса
 сек,
сек,
Запасы устойчивости: по амплитуде 15.9 дБ, по фазе 60.2 градусов.
В сравнении с П-регулятором, использование ПД-регулятора позволяет …
4.2 Регулятор, обеспечивающий кратчайший переходный процесс
Для обеспечения минимального времени переходного процесса требуется выбрать

Переходная функция скорректированной замкнутой системы

Время переходного процесса
 сек,
сек,
Запасы устойчивости: по амплитуде 18.4 дБ, по фазе 67.3 градуса.
Передаточная функция замкнутой системы
0.025771 (s+0.05208) (s+0.1667)
-------------------------------------------------------------
(s+0.9892) (s+0.5459) (s+0.04826) (s^2 + 0.1382s + 0.008584)
Порядок передаточной функции равен 5, потому что …
Полюса передаточной функции
-0.9892
-0.5459
-0.0691 + 0.0617i
-0.0691 - 0.0617i
-0.0483
Близость полюсов к мнимой оси означает, что … При этом запас устойчивости …
Коэффициент усиления системы в установившемся режиме равен … Это объясняется тем, что …
При постоянном сигнала установившаяся ошибка …, потому что …
При линейно возрастающем сигнале установившаяся ошибка …, потому что …
При использовании датчика, описываемого моделью , коэффициент усиления в установившемся режиме будет равен …, потому что …
Полученная система является астатической, то есть, отслеживает без ошибки постоянный входной сигнал. Это определяется тем, что …
При линейно возрастающем сигнале …
Передаточная функция замкнутой системы от входа к сигналу управления
13.5168 s (s+0.05208) (s+0.05495) (s+0.1667) (s+0.5)
-------------------------------------------------------------
(s+0.9892) (s+0.5459) (s+0.04826) (s^2 + 0.1382s + 0.008584)
Изменение сигнала управления при единичном ступенчатом входном сигнале

Сигнал управления стремится к нулю, потому что …
Самостоятельная работа студента с преподавателем № 3 (5, 6 недели обучения) Моделирование систем управления в пакете Simulink Создание моделей в Simulink
Пакет Simulink предназначен для моделирования систем. Вся модель строится из блоков, имеющих входы и выходы. Существует библиотека стандартных блоков, кроме того, можно создавать свои собственные блоки любой сложности. Существует две группы специальных устройств – источники сигналов (Sources) и устройства вывода (Sinks).
Блоки имеют названия. Для того, чтобы изменить название, надо щелкнуть по нему ЛКМ и отредактировать текст16.
Каждый блок имеет свои настраиваемые свойства. Для их изменения надо дважды щелкнуть на блоке и изменить нужные значения в диалоговом окне.
Для того, чтобы повернуть блок на 90 градусов, надо выделить его и нажать клавиши Ctrl+R. Комбинация Ctrl+I позволяет выполнить зеркальное отражение входов и выходов.
Верхнее меню Format предназначено для изменения оформления выделенного блока. Также для этой цели можно использовать контекстное меню ПКМ – Format. Для выделенного блока можно изменить цвет текста и линий (Foreground color), цвет фона (Background color), вывести тень (Show drop shadow), переместить название на другую сторону (Flip name).
Для выделения одного блока или соединительной линии надо щелкнуть ЛКМ по нужному элементу. Для того, чтобы выделить несколько блоков, надо «обвести» их при нажатой ЛКМ. Клавиша Delete удаляют выделенную часть. Чтобы скопировать блок (или выделенную часть), надо перетащить его при нажатой правой кнопке мыши (ПКМ).
Блоки соединяются линиями связи, по которым распространяются сигналы. Для того, чтобы соединить блоки, надо щелкнуть ЛКМ по источнику сигнала и затем, при нажатой клавише Ctrl, по блоку-приемнику. Можно также протянуть мышкой линию связи между нужными выходом и входом.
Чтобы подать один сигнал на два блока (сделать «развилку»), надо сначала создать одну линию обычным способом. Чтобы провести вторую линию, следует нажать правую кнопку мыши на линии в точке развилки и протащить линию ко второму блоку.
Модель можно скопировать в буфер обмена в виде растрового рисунка. Для этого в окне модели надо выбрать в верхнем меню пункт Edit – Copy model to clipboard. Предварительно лучше уменьшить размеры окна до минимальных, чтобы не было белых полей.
Для того, чтобы запустить моделирование,
надо щелкнуть ЛКМ по кнопке
![]() на панели инструментов. Эта же кнопка
позволяет остановить моделирование
при необходимости.
на панели инструментов. Эта же кнопка
позволяет остановить моделирование
при необходимости.
Параметры моделирования (метод интегрирования, обработка ошибок) устанавливаются с помощью окна Simulation – Parameters. Самые важные параметры – это время моделирования (Stop time) и метод численного интегрирования уравнений (Solver options).
Основные источники сигналов (Sources)
|
Constant – сигнал постоянной величины. |
|
Step – ступенчатый сигнал, меняется время скачка (Step Time), начальное (Initial Value) и конечное значение (Final Value). |
|
Ramp – линейно возрастающий сигнал с заданным наклоном (Slope). Можно задать также время начала изменения сигнала (Start Time) и начальное значение (Initial Value). |
|
Pulse Generator – генератор прямоугольных импульсов, задаются амплитуда (Amplitude), период (Period), ширина (Pulse Width, в процентах от периода), фаза (Phase Delay). |
|
Repeating Sequence – последовательность импульсов, их форма задается в виде пар чисел (время; величина сигнала) |
|
Sine Wave – синусоидальный сигнал, задается амплитуда (Amplitude), частота (Frequency), фаза (Phase) и среднее значение (Bias). |
|
Signal Builder – построитель сигналов, позволяющий задавать форму сигнала, перетаскивая мышью опорные точки. |
|
Random Number – случайные числа с нормальным (гауссовым) распределением. Можно задать среднее значение (Mean Value), дисперсию (Variance), период изменения сигнала (Sample Time). |
|
Uniform Random Number – случайные числа с равномерным распределением в заданном интервале от Minimum до Maximum. |
|
Band Limited White Noise – случайный сигнал, ограниченный по полосе белый шум (имеющий равномерный спектр до некоторой частоты). Блок используется как источник белого шума для моделей непрерывных систем. Задается интенсивность (Noise Power) и интервал дискретизации (Sample Time), в течение которого удерживается постоянное значение сигнала. Чем меньше интервал, тем точнее моделирование, однако больше вычислительные затраты. |
Основные устройства вывода (Sinks)
|
Display – цифровой дисплей, показывает изменение входного сигнала в цифровом виде. |
|
Scope – осциллограф, показывает изменение сигнала в виде графика, позволяет передавать данные в рабочую область Matlab для последующей обработки и оформления. |
Линейные системы (Continuous)
|
Transfer Fcn – передаточная функция, в параметрах задаются числитель (Numerator) и знаменатель (Denominator) в виде полиномов. |
|
State Space – модель в пространстве состояний, в параметрах задается четверка матриц, определяющих модель, и начальные условия для вектора состояния (Initial conditions). |
|
Zero-Pole – модель в форме «нули-полюса», в параметрах задаются массивы нулей (Zeros), полюсов (Poles), а также коэффициент усиления (Gain). |
|
Integrator – интегратор с возможностью установки начальных условий (Initial condition), а также пределов насыщения (Lower saturation limit и Upper saturation limit). Когда сигнал выхода выходит за границы, определяемые этими пределами, интегрирование прекращается. |
Другие часто используемые блоки
Math Operations
-

Gain – усилитель, задается коэффициент усиления (Gain).

Sum – сумматор, используется для сложения и вычитания входов. Параметр List of signs задает количество входов, их знаки («+» для сложения и «–» для вычитания). Промежутки между входами (обозначаются знаком |).

Trigonometric Function – тригонометрическая функция.
Signal Routing
-

Manual Switch – ручной переключатель, позволяет двойным щелчком переключать выход на один из двух входных сигналов.

Mux – мультиплексор, объединяет несколько сигналов в один «жгут» (векторный сигнал), в параметрах задается число входов (Number of Inputs).

Demux – демультиплексор, позволяет «разбить» векторный сигнал на несколько скалярных, в параметрах задается число выходов (Number of Outputs).
Блок Scope
В окне блока Scope
изображается график изменения входного
сигнала. Если вход соединен с выходом
мультиплексора, сразу строится несколько
графиков (по размерности входного
«жгута»).
окне блока Scope
изображается график изменения входного
сигнала. Если вход соединен с выходом
мультиплексора, сразу строится несколько
графиков (по размерности входного
«жгута»).
По умолчанию на оси ординат используется
диапазон от -5 до 5. Если этот вариант не
подходит, выбрать масштаб автоматически
(так, чтобы весь график был виден) можно
с помощью кнопки
![]() .
Соседняя кнопка
.
Соседняя кнопка
![]() сохраняет эти настройки для следующих
запусков.
сохраняет эти настройки для следующих
запусков.
Кнопка
![]() открывает окно настроек, причем наиболее
важные данные содержатся на вкладке
Data history.
Если не сбросить флажок Limit
data points,
в памяти будет сохраняться только
заданное число точек графика, то есть,
при большом времени моделирования
начало графика будет потеряно.
открывает окно настроек, причем наиболее
важные данные содержатся на вкладке
Data history.
Если не сбросить флажок Limit
data points,
в памяти будет сохраняться только
заданное число точек графика, то есть,
при большом времени моделирования
начало графика будет потеряно.
Отметив на этой же странице флажок Save data to workspace можно сразу передать результаты моделирования в рабочую область Matlab для того, чтобы их можно было дальше обрабатывать, выводить на графики и сохранять в файле. Поле Variable name задает имя переменной в рабочей области, в которой сохраняются данные. В простейшем случае выбирается формат Array (в списке Format). Это означает, что данные будут сохраняться в массиве из нескольких столбцов (первый столбец – время, второй – первый сигнал, третий – второй сигнал и т.д., по порядку входов мультиплексора).
Оформление графиков
Для создания нового окна для рисунка в Matlab используется команда
>> figure(1);
Вместо единицы можно ставить любой номер рисунка. Если рисунок с таким номером уже есть, он становится активным и выводится на первый план. Если такого рисунка нет, он создается и становится активным.
В Matlab есть возможность строить несколько графиков на одном рисунке. Иначе говоря, рисунок можно разбить на «клетки», в каждой из которых строится отдельный график. Для этого надо сделать активным нужный рисунок и применить команду
>> subplot(2, 1, 1);
Первое число в команде subplot показывает количество «строк» в такой матрице, второе – количество столбцов, третье – какой по счету график сделать активным (считая по строкам, справа налево и сверху вниз). Все дальнейшие команды (plot, title, xlabel, ylabel, legend и др.) относятся к этому «подграфику».
В командах можно передавать в качестве аргументов не целые массивы, а их части. Например, по команде
>> plot(x(1:20), y(11:30));
строится график, на котором по оси абсцисс откладываются значения элементов массива x с номерами от 1 до 20, а по оси ординат – соответствующие им значения из массива y с номерами от 11 до 30.
Двоеточие означает «все строки» или «все столбцы». Например, по команде
>> plot(x(:,1), x(:,2));
строится зависимость между первым и вторым столбцами массива x (здесь двоеточие вместо первого индекса обозначает «все строки»).
С помощью команды plot (а также и других подобных – semilogx, semilogy, loglog) можно строить несколько линий на одном графике. Для этого среди аргументов перечисляются пары массивов:
>> plot(x, y, v, z);
Первая линия будет показывать зависимость y от x, а вторая – зависимость z от v. массивы в каждой паре должны быть одинаковой длины. При желании можно указать цвета для каждой линии, Например,
>> plot(x, y, 'b', v, z, 'g');
Первая линия (зависимость y от x) будет синей, вторая (зависимость z от v) – зеленой. Можно использовать следующие цвета
b синий (blue)
g зеленый (green)
r красный (red)
c голубой (cyan)
m фиолетовый (magenta)
y желтый (yellow)
k черный (black)
По умолчанию первая линия – синяя, вторая – зеленая и т.д. в порядке перечисления цветов в списке. Дополнительно можно указать тип линии
- сплошная
: точечная
-. штрих-пунктирная
-- штриховая
Например,
>> plot(x, y, 'b:', v, z,'g--');
Первая линия – точечная синего цвета, вторая – штриховая зеленого цвета. По умолчанию все линии сплошные.
Для оформления графика также используются команды
title заголовок графика
xlabel название оси абсцисс
ylabel название оси ординат
У всех этих команд обязателен один аргумент – текст в апострофах.
Команда legend служит для вывода легенды графика. Легенда нужна, если на графике есть несколько линий и надо показать, что обозначает каждая из них. Параметрами команды legend являются символьные строки, их должно быть столько, сколько построено линий.
В надписях можно использовать некоторые
команды системы ТеХ17.
Например, греческие буквы записываются
в виде «\alpha»,
«\beta» и т.д. Верхний
индекс (степень) обозначается знаком
«^», Например,
 запишется как «a^2».
Для обозначения индекса используют
нижнее подчеркивание, например,
запишется как «a^2».
Для обозначения индекса используют
нижнее подчеркивание, например,
 кодируется как «a_{22}».
кодируется как «a_{22}».
Компенсация постоянных возмущений
На любое судно в реальных условиях действуют возмущающие силы, вызванные ветром, морским волнением и другими причинами. Некоторые из них (например, влияние ветра) содержат постоянную составляющую, т.е., их среднее значение не равно нулю. Тем не менее, система управления должна поддерживать заданный курс судна даже в таких условиях. Возмущающие силы и моменты приложены непосредственно к входу объекта управления, т.е., структурная схема имеет такой вид:

Подавление возмущений (обозначенных
на схеме через
 )
определяется передаточной функцией
системы по возмущению, т.е., передаточной
функцией от входа w к
выходу
:
)
определяется передаточной функцией
системы по возмущению, т.е., передаточной
функцией от входа w к
выходу
:
 .
.
Если она содержит нуль в точке , соответствующая АЧХ равна нулю на нулевой частоте, т.е., постоянные возмущения в установившемся режиме компенсируются полностью. Для этого требуется, чтобы интегратор входил в модель привода, обратной связи или регулятора. Таким образом, если регулятор содержит интегральный канал (И-канал), в системе нет статической ошибки при постоянном возмущении .
Моделирование систем управления в пакете Simulink Цели работы
освоение методов моделирования линейных систем в пакете Simulink
Задачи работы
научиться строить и редактировать модели систем управления в пакете Simulink
научиться изменять параметры блоков
научиться строить переходные процессы
научиться оформлять результаты моделирования
изучить метод компенсации постоянных возмущений с помощью ПИД-регулятора
Оформление отчета
Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать
название предмета, номер и название лабораторной работы
фамилию и инициалы авторов, номер группы
фамилию и инициалы преподавателя
номер варианта
краткое описание исследуемой системы
результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.
При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.
Описание системы
В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.
Структурная схема системы стабилизации судна на курсе
Линейная математическая модель, описывающая рыскание судна, имеет вид
где – угол рыскания (угол отклонения от заданного курса), – угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, – постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
.
Привод (рулевая машина) приближенно моделируется как интегрирующее звено, охваченное единичной отрицательной обратной связью, так что его передаточная функция равна
 .
.
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией18
.
Исследуются переходные процессы в системе при использовании ПД-регулятора
 ,
,
и ПИД-регулятора
 .
.
Инструкция по выполнению работы
Этап выполнения задания |
Команды Matlab |
|
simulink |
|
File – New – Model |
|
Двойной щелчок на блоке
|
|
ЛКМ на имени блока |
|
|
|
File – Save |
|
Нажать Ctrl+I или дважды нажать Ctrl+R. |
|
ПКМ на блоке, Format - Flip name |
|
ПКМ на блоке, Format – Background color |
|
ЛКМ |
|
Двойной щелчок на блоке, ввести |+- в поле List of signs |
|
|
|
Двойной щелчок на блоке, 0 в поле Step time 10 в поле Final value |
|
ЛКМ на источнике, удерживать Ctrl и ЛКМ на приемнике, или протащить ЛКМ от выхода одного блока к входу другого |
|
|
|
Нажать ПКМ на линии в точке отбора сигнала, затем, не отпуская ПКМ, тащить линию к входу блока. |
|
Edit – Copy model to clipboard
|
|
Simulation – Simulation parameters 100 в поле Stop time |
|
ЛКМ по кнопке |
|
Двойной щелчок по блоку |
|
|
|
ЛКМ по кнопке |
|
ЛКМ по кнопке вкладка Data history
Variable name: phi (Курс) или delta (Руль) Format: Array |
|
ЛКМ по кнопке |
|
figure(1); |
|
subplot(2, 1, 1); |
|
plot(phi(:,1),phi(:,2)); |
|
title('Курс'); |
|
xlabel('Время, сек'); ylabel('\phi, градусы'); |
|
subplot(2, 1, 2); plot(delta(:,1),delta(:,2)); title('Угол поворота руля'); xlabel('Время, сек'); ylabel('\delta, градусы'); |
|
print -dmeta |
|
ЛКМ по линии, нажать Delete. |
|
Двойной щелчок по блоку ++| в поле List of signs |
|
|
|
Перетаскивание ПКМ. Двойной щелчок по блоку 2 в поле Final Value Двойной щелчок по имени |
|
Edit – Copy model to clipboard |
|
Simulation – Simulation parameters - Stop time ЛКМ по кнопке |
|
|
|
|
|
phi0 = phi; delta0 = delta; |
|
|
|
ЛКМ по кнопке |
|
|
|
|
|
subplot(2, 1, 1); plot(phi0(:,1), phi0(:,2),... phi (:,1), phi(:,2)); title('Курс'); xlabel('Время, сек'); ylabel('\phi, градусы'); legend('ПД-регулятор', ... 'ПИД-регулятор'); |
|
|
|
|
|
|
|
[gm,phim] = margin(W) gm = 20*log10(gm) |
Таблица коэффициентов
Вариант |
, сек |
, рад/сек |
, сек |
, сек |
|
|
16.0 |
0.06 |
1 |
1 |
|
|
16.2 |
0.07 |
2 |
2 |
|
|
16.4 |
0.08 |
1 |
3 |
|
|
16.6 |
0.07 |
2 |
4 |
|
|
16.8 |
0.06 |
1 |
5 |
|
|
17.0 |
0.07 |
2 |
6 |
|
|
17.2 |
0.08 |
1 |
1 |
|
|
17.4 |
0.07 |
2 |
2 |
|
|
17.6 |
0.06 |
1 |
3 |
|
|
17.8 |
0.07 |
2 |
4 |
|
|
18.0 |
0.08 |
1 |
5 |
|
|
18.2 |
0.09 |
2 |
6 |
|
|
18.4 |
0.10 |
1 |
1 |
|
|
18.6 |
0.09 |
2 |
2 |
|
|
18.8 |
0.08 |
1 |
3 |
|
|
19.0 |
0.07 |
2 |
4 |
|
|
19.2 |
0.08 |
1 |
5 |
|
|
19.4 |
0.09 |
2 |
6 |
|
|
19.6 |
0.10 |
1 |
1 |
|
|
18.2 |
0.0694 |
2 |
6 |
Контрольные вопросы к защите
См. все вопросы к работам № 1 и № 2.
Как найти передаточную функцию интегратора, охваченного обратной связью?
Как запустить пакет Simulink?
Что такое Library Browser?
Какое расширение имеют файлы – модели Simulink?
Как создать новую модель?
Как соединить два блока, имеющих соответственно свободный выход и свободный вход?
Как сделать, чтобы один и тот же сигнал поступал на несколько блоков?
Как передать результаты моделирования в рабочую область Matlab? В каком виде они передаются?
Как удалить блок или связь между блоками?
Как определить нужные масштабы для осей координат в окнах Scope и запомнить их?
Как скопировать блок в окне модели?
Как изменить знаки арифметических действий в сумматоре?
Как скопировать изображение модели в документ Microsoft Word?
Как изменить время моделирования?
Как изменить название у блока?
Как сделать, чтобы название блока было с другой стороны?
Как изменить цвет фона блока? цвет надписи?
Как ввести параметры блока Transfer Fcn (передаточная функция)?
Как найти передаточную функцию системы по возмущению?
Почему при использовании ПД-регулятора система не компенсирует постоянное возмущение?
Как, зная статический коэффициент усиления по возмущению, определить установившееся отклонение от заданного курса?
Какими свойствами должна обладать передаточная функция по возмущению для того, чтобы постоянное возмущение полностью компенсировалось?
Какими свойствами должен обладать регулятор для того, чтобы постоянное возмущение полностью компенсировалось?
Какие преимущества дает использование интегрального канала в ПИД-регуляторе?
Почему порядок передаточной функции замкнутой системы по возмущению с ПИД-регулятором на 1 больше, чем для системы с ПД-регулятором?
Какие параметры принимает команда subplot?
Что означает двоеточие в записи phi(:,1)?
Как вывести на график заголовок и названия осей?
Как построить в одном окне два разных графика?
Как на одном графике построить несколько кривых?
Что такое легенда? Как вывести легенду на график?
Как выводить на графике буквы греческого алфавита?
Пример оформления отчета. Моделирование систем управления в пакете Simulink
1.Описание системы
Исследуется система управления судном по курсу, структурная схема которой показана на рисунке.
Движение судна описывается линейной математической моделью в виде передаточной функции
, где рад/сек, сек,
Привод моделируется как интегрирующее звено, охваченное единичной отрицательной обратной связью, так что его передаточная функция равна
 ,
сек,
,
сек,
Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией
, сек,
Исследование системы с пд-регулятором
передаточная функция ПД-регулятора, обеспечивающего переходный процесс минимальной длительности
,
где
 ,
сек,
сек,
,
сек,
сек,
модель системы с ПД-регулятором
переходные процессы в системе с ПД-регулятором при изменении курса на 10 градусов
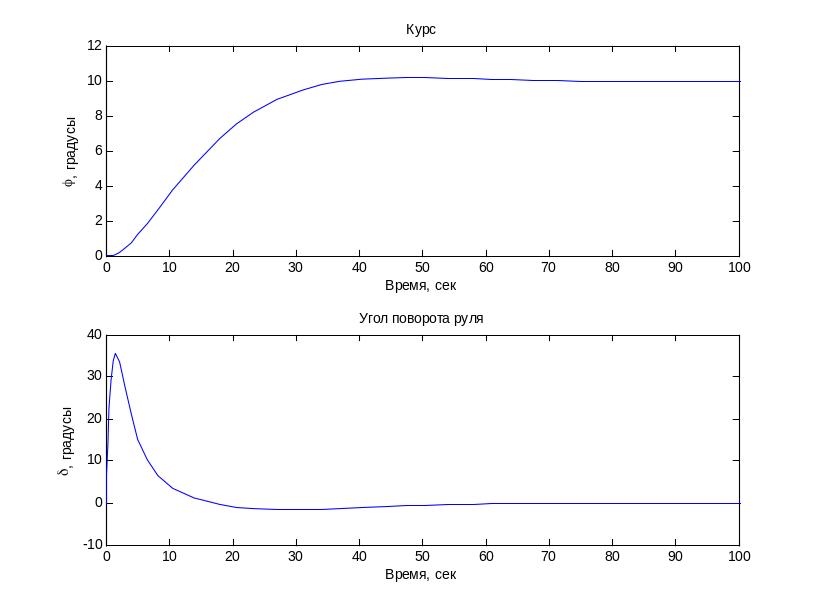
модель системы с ПД-регулятором с учетом внешнего возмущения
передаточная функция по возмущению для системы с ПД-регулятором
0.003813 s^3 + 0.006355 s^2 + 0.00286 s + 0.0003178
------------------------------------------------------------------
s^5 + 1.722 s^4 + 0.8416 s^3 + 0.1245 s^2 + 0.008877 s + 0.0002239
судно с ПД-регулятором не вышло на заданный курс 10 градусов, потому что …
статический коэффициент усиления
 ,
установившееся значение сигнала выхода
должно быть равно
,
установившееся значение сигнала выхода
должно быть равно
 ,
потому что …; эти данные согласуются
с результатами моделирования
,
потому что …; эти данные согласуются
с результатами моделирования
3.Исследование системы с пид-регулятором
передаточная функция ПИД-регулятора
,
где
,
сек,
сек,
 сек,
сек,
модель системы с ПИД-регулятором с учетом внешнего возмущения
передаточная функция по возмущению для системы с ПИД-регулятором
0.003813 s^4 + 0.006355 s^3 + 0.00286 s^2 + 0.0003178 s
-----------------------------------------------------------------------------------
s^6 + 1.722 s^5 + 0.8416 s^4 + 0.1245 s^3 + 0.008877 s^2 + 0.0002255 s + 1.589e-006
при использовании ПИД-регулятора судно выходит на заданный курс, потому что …
статический коэффициент усиления
 ,
установившееся значение сигнала выхода
должно быть равно
,
потому что …; эти данные согласуются
с результатами моделирования
,
установившееся значение сигнала выхода
должно быть равно
,
потому что …; эти данные согласуются
с результатами моделированияпереходные процессы в системах с ПД- и ПИД-регуляторами

при использовании ПИД-регулятора вместо ПД-регулятора … (что улучшилось?),
при этом сигнал управления … (как изменился?)
в то же время … (что ухудшилось?)
передаточная функция разомкнутой системы с ПИД-регулятором
0.004298 s^2 + 0.0002255 s + 1.589e-006
--------------------------------------------------------
s^6 + 1.722 s^5 + 0.8416 s^4 + 0.1245 s^3 + 0.004579 s^2
запас устойчивости по амплитуде
 дБ,
по фазе
дБ,
по фазе
 ,
запасы являются достаточными
,
запасы являются достаточными
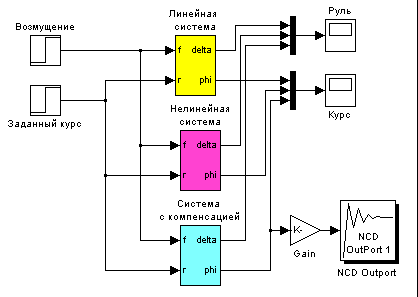
Самостоятельная работа студента с преподавателем № 4 (7, 8 недели обучения) Моделирование нелинейных систем управления Модели нелинейных звеньев (Discontinuities)
|
Saturation – насыщение, в параметрах задаются верхний и нижний пределы (Upper limit и Lower limit). |
|
Dead zone – нечувствительность, «мертвая зона». В параметрах задаются пределы нечувствительности (Start of dead zone и End of dead zone). |
|
Rate Limiter – ограничитель скорости изменения сигнала, в параметрах задаются пределы на скорость увеличения (Rising slew rate) и на скорость уменьшения (Falling slew rate). |
|
Relay – реле, в параметрах задаются точки переключения (Switch on point и Switch off point), в также величины сигналов в режимах «включено» (Output when on) и «выключено» (Output when off). |
|
Backlash – люфт, «мертвый ход». В параметрах задаются величина мертвого хода (Deadband width) и начальное значение выхода (Initial output). |
|
Coulomb and Viscous Friction – кулоновское и вязкое трение. |
Подсистемы
Если на схеме много блоков, она становится громоздкой и работать с такой схемой неудобно. Чтобы не перегружать схемы, можно объединять блоки в подсистемы. Проще всего выделить нужные блоки мышкой («обвести» при нажатой ЛКМ) и нажать клавиши Ctrl+G (или выбрать пункт меню Edit – Create subsystem). На основной схеме подсистема изображается как блок типа Subsystem (из группы Ports and Subsystems). Этот блок можно добавить и вручную, перетащив из окна Library Browser.
С помощью двойного щелчка ЛКМ можно «открыть» подсистему. Входы обозначаются блоками In, а выходы – блоками Out (также из группы Ports and Subsystems). Можно добавлять новые входы и выходы, удалять ненужные, менять названия, работая с ними так же, как с остальными блоками.
Внутри подсистем можно создавать вложенные подсистемы. В подсистеме не может быть блоков с одинаковыми названиями, однако в разных подсистемах – могут быть.
С охранить
модель можно из окна любой подсистемы,
но закрытие окна подсистемы не приводит
к закрытию модели.
охранить
модель можно из окна любой подсистемы,
но закрытие окна подсистемы не приводит
к закрытию модели.
Б лок Scope (несколько сигналов)
К входу осциллографа (блока Scope) можно подключать несколько сигналов одновременно. Для этого их надо объединить в один векторный сигнал («жгут») с помощью блока Mux (мультиплексор) из группы Signal Routing.
Если используется два входных сигнала, первый изображается желтой линией, второй – фиолетовой. При передаче данных в рабочую область Matlab в формате Array, массив будет содержать три столбца – время, первый сигнал и второй сигнал. Если сигналов больше, соответственно увеличивается количество столбцов массива.
Скрипты
При работе в Matlab часто для получения нужного результата надо ввести последовательно несколько команд. Если выяснится, что в какой-то команде была сделана ошибка или нужно изменить исходные данные, все команды придется вводить снова. Чтобы не набирать их вручную, можно записать всю последовательность команд на диск в виде текстового файла (М-файла с расширением .m), а затем выполнять его, вызывая по имени. Такой файл называется скриптом.
Скрипт – это программа, которая представляет собой список команд на языке системы Matlab. Скрипты можно создавать и редактировать в любом простейшем текстовом редакторе (например, в Блокноте), однако удобнее всего использовать встроенный редактор Matlab, в котором есть подсветка синтаксиса (команды, символьные строки, комментарии и другие элементы программы выделяются разными цветами).
В М-файле перечисляются последовательно все необходимые команды. Точка с запятой в конце команды подавляет вывод результата на экран. Можно располагать в одной строке несколько команд, разделяя их запятой (если нужен вывод результата на экран) или точкой с запятой. Если надо перенести длинную команду на следующую строчку, в конце строки ставится троеточие.
Комментарием считается все, что расположено справа от знака % до конца строки. Его можно ставить в любом месте строки, например, справа от команды Matlab.
Для вызова скрипта надо набрать его имя в командном окне Matlab и нажать клавишу Enter. Скрипт должен находиться в рабочей папке (имя которой показано в окне Current directory в верхней части командного окна) или в одной из папок, входящих в путь для поиска. В путь для поиска включены папки, в которых находятся М-файлы для стандартных функций системы Matlab и дополнительных пакетов (toolbox). Если надо, чтобы скрипт запускался из любой папки, надо включить папку, где он находится, в путь для поиска (команда File – Set Path верхнего меню).
Запустить скрипт можно непосредственно из окна редактора Matlab, нажав на клавишу F5. Можно выполнить не весь скрипт, а только некоторые строки – их нужно выделить и нажать клавишу F9. Можно расположить два окна (редактор и командное окно Matlab) рядом так, чтобы они не перекрывали друг друга. Тогда при выполнении скрипта (или отдельных команд) сразу будет виден результат.
Если в командах скрипта есть ошибки (или они возникли при выполнении), соответствующие сообщения выводятся в командное окно Matlab.
Форматирование графика
По умолчанию команда plot рисует на активном графике новую кривую, стирая старые линии. Для того, чтобы существующие кривые сохранились, перед вызовом plot надо выполнить команду
>> hold on
Обратная ей команда
>> hold off
восстанавливает стандартный режим.
Каждый объект на графике (оси координат, надписи, линии и т.п.) представляют собой объекты, имеющие свойства. Для того, чтобы получить значение свойства, используют команду get, а для изменение свойства – команду set. Сокращение gca обозначает текущие (активные) оси координат (get current axes). Команда
>> get(gca)
выводит на экран все свойства осей и их значения. Для управления размером шрифта (он измеряется в пунктах) используется свойство Font Size:
>> get(gca, ‘FontSize’) % определить размер шрифта
ans =
10
>> set(gca, ‘FontSize’, 16) % изменить размер шрифта
Для того, чтобы настроить свойства отдельной линии, надо сначала получить ее хэндл (handle – ручка, рукоятка, указатель). Так называется уникальный числовой код объекта, через который к этому объекту можно обращаться. Команда gca в самом деле возвращает хэндл текущих координатных осей. Команда
>> h = get(gca, 'Children')
записывает в переменную h массив хэндлов – указателей на объекты линии. Для каждой линии можно установить толщину (в пунктах, по умолчанию – 0,5 пункта) .
>> set(h(1),'LineWidth',1.5)
>> set(h(2),'LineWidth',1.5)
Аналогично можно управлять и другими свойствами.
Лабораторная работа № 4 Моделирование нелинейных систем управления Цели работы
освоение методов моделирования нелинейных систем в пакете Simulink
Задачи работы
научиться строить и редактировать модели с подсистемами
научиться использовать нелинейные звенья типа «насыщение»
научиться строить несколько графиков одновременно на одном осциллографе
научиться составлять, редактировать и отлаживать скрипты
научиться изменять свойства элементов графика (шрифт, толщину линии)
Оформление отчета
Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать
название предмета, номер и название лабораторной работы
фамилию и инициалы авторов, номер группы
фамилию и инициалы преподавателя
номер варианта
краткое описание исследуемой системы
результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.
При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.
Описание системы
В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.

Структурная схема системы стабилизации судна на курсе
Линейная математическая модель, описывающая рыскание судна, имеет вид
где – угол рыскания (угол отклонения от заданного курса), – угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, – постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
.
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
 ,
,
 .
.
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией21
,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией22
 ,
где
сек
и
сек.
,
где
сек
и
сек.
Инструкция по выполнению работы
Этап выполнения задания |
Команды Matlab |
|
ЛКМ по кнопке
|
|
View – Current directory |
|
двойной щелчок на lab3.mdl |
|
File – Save as ... |
|
Edit – Create subsystem |
|
Двойной щелчок на имени ПКМ – Format – Flip name ПКМ – Background color |
|
Двойной щелчок на блоке ЛКМ на имени входа или выхода |
|
|
|
Edit – Create subsystem |
|
Перетащить с помощью ПКМ Format – Background color |
|
Двойной щелчок на блоке |
|
ЛКМ на элементе, нажать Delete. |
|
Двойной щелчок на блоке
|
|
View – Library Browser |
|
Двойной щелчок на блоке |+- в поле List of signs |
|
|
|
Двойной щелчок на блоке
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
File – New – M-file |
|
figure(1); % открыть рис. 1 subplot(2,1,1); plot(phi(:,1),phi(:,2),'b'); hold on; plot(phi(:,1),phi(:,3),'g'); hold off; legend('Линейная система', ... 'Нелинейная система') |
|
File - Save |
|
клавиша F5 |
|
set(gca,'FontSize',16); |
|
title('Поворот на 10 градусов') xlabel('Время, сек'); ylabel('\phi, град'); |
|
h = get(gca, 'Children') set(h(1),'LineWidth',1.5) set(h(2),'LineWidth',1.5) |
|
|
|
|
|
|
|
Двойной щелчок на блоке Заданный курс ввести 90 в поле Final value |
|
title('Поворот на 90 градусов') клавиша F5 print -dmeta |
|
|
Таблица коэффициентов
Вариант |
, сек |
, рад/сек |
, сек |
, сек |
|
|
16.0 |
0.06 |
1 |
1 |
|
|
16.2 |
0.07 |
2 |
2 |
|
|
16.4 |
0.08 |
1 |
3 |
|
|
16.6 |
0.07 |
2 |
4 |
|
|
16.8 |
0.06 |
1 |
5 |
|
|
17.0 |
0.07 |
2 |
6 |
|
|
17.2 |
0.08 |
1 |
1 |
|
|
17.4 |
0.07 |
2 |
2 |
|
|
17.6 |
0.06 |
1 |
3 |
|
|
17.8 |
0.07 |
2 |
4 |
|
|
18.0 |
0.08 |
1 |
5 |
|
|
18.2 |
0.09 |
2 |
6 |
|
|
18.4 |
0.10 |
1 |
1 |
|
|
18.6 |
0.09 |
2 |
2 |
|
|
18.8 |
0.08 |
1 |
3 |
|
|
19.0 |
0.07 |
2 |
4 |
|
|
19.2 |
0.08 |
1 |
5 |
|
|
19.4 |
0.09 |
2 |
6 |
|
|
19.6 |
0.10 |
1 |
1 |
|
|
18.2 |
0.0694 |
2 |
6 |
Контрольные вопросы к защите
См. все вопросы к работам № 1, № 2 и № 3.
Как построить подсистему из нескольких существующих блоков модели?
Сколько входов и выходов может иметь подсистема?
Как редактировать подсистему?
Как изменить названия входов и выходов подсистемы?
Как скопировать существующий блок или подсистему?
Как удалить блок или соединительную линию?
Объясните структуру нелинейной модели привода.
Почему в нелинейной модели нельзя использовать общую передаточную функцию линейной модели привода ?
Как выбираются пределы насыщения для блока, расположенного на входе интегратора?
Как освободить блок от связей с другими блоками?
Объясните назначение блока Mux.
Как разобраться, какой сигнал поступает на первый вход осциллографа (через мультиплексор), какой – на второй?
Что такое скрипт в среде Matlab?
Что означает знак % внутри скрипта?
Как вводить несколько команд в одной строке?
Как правильно перенести длинную команду на следующую строку?
Что означает третий параметр при вызове функции plot?
Что означают команды hold on и hold off?
Как запустить скрипт на выполнение?
Как выполнить только некоторые команды из скрипта?
Что означает gca?
Для чего служат функции set и get?
Как узнать и изменить размер шрифта на графике?
Зачем нужен хэндл (handle) графического объекта?
Как изменить толщину линии на графике?
Где выводятся сообщения об ошибках в скрипте?
Пример оформления отчета. Моделирование нелинейных систем управления
1.Описание системы
Исследуется нелинейная система управления судном по курсу, структурная схема которой показана на рисунке.

Движение судна описывается линейной математической моделью в виде передаточной функции
, где рад/сек, сек,
Линейная модель привода представляет собой интегрирующее звено с передаточной функцией
, сек,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией
, сек,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией
,
где , сек, сек, сек,
2.Построение нелинейной модели
модель системы управления с выделенными подсистемами
нелинейная модель привода
нижний и верхний пределы насыщения
блок Saturation: от
 до
до

блок Saturation1: от
 до
до

эти величины объясняются тем, что …
3.Сравнение линейной и нелинейной моделей
структурная схема системы для сравнения линейной и нелинейной моделей
скрипт для построения и оформления графиков
close(1);
figure(1);
subplot(2,1,1);
...
set(h(1),'LineWidth',1.5)
set(h(2),'LineWidth',1.5)
переходные процессы при изменении курса на 10 градусов

расхождение между результатами моделирования линейной и нелинейной системы объясняется тем, что …
наибольшее влияние оказывает … (какая нелинейность?), потому что …
в то же время … (что можно сказать о второй нелинейности?)
переходные процессы при изменении курса на 90 градусов
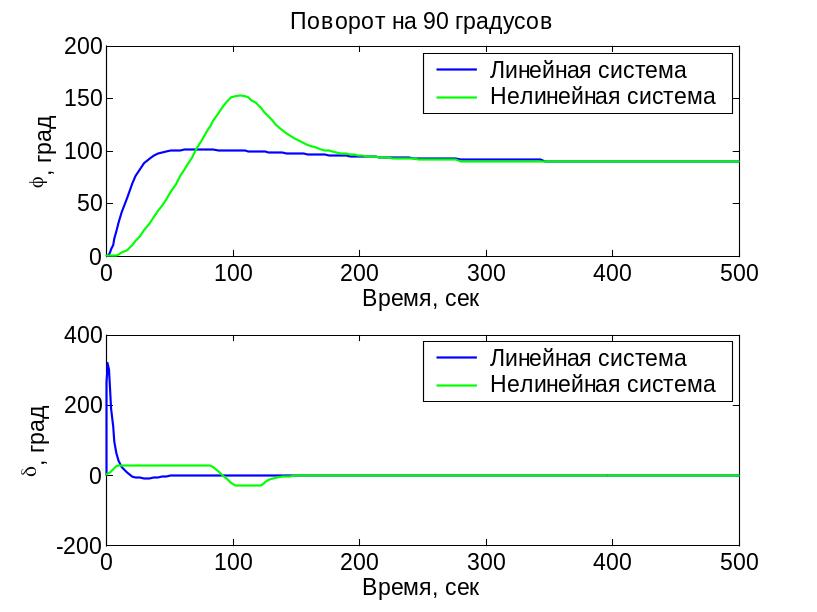
при больших углах поворота наблюдается существенное расхождение между процессами в линейной и нелинейной системах, потому что …
в этом случае … (как влияют нелинейности?)
Самостоятельная работа студентов с преподавателем № 5 (9, 10 недели обучения) Программирование в среде Matlab Передача данных в модель Simulink
Если параметры блоков модели часто изменяются, удобнее сделать так, чтобы их можно было менять прямо в командном окне Matlab или даже из скрипта. Для этого при задании параметров блоков надо использовать не числовые значения, а имена переменных. При запуске моделирования Simulink будет искать переменные с такими именами в рабочей области Matlab и подставлять их значения. Например, в параметрах блока Transfer Fcn можно задать
Numerator: n
Denominator: d
Тогда для того, чтобы звено соответствовало
передаточной функции
 в командном окне Matlab
надо задать значения для этих массивов
в командном окне Matlab
надо задать значения для этих массивов
>> n = [1 2]
n =
1 2
>> d = [2 3 1]
d =
2 3 1
При любом изменении этих массивов в
рабочей области меняются и свойства
соответствующего блока в модели. Можно
использовать и более сложные выражения,
например, в поле Numerator
можно ввести Kc*[Ts
1 0]. Это означает, что числитель имеет
вид
 ,
при старте моделирования из рабочей
области Matlab
будут загружены значения двух переменные
с именами Kc и Ts.
,
при старте моделирования из рабочей
области Matlab
будут загружены значения двух переменные
с именами Kc и Ts.
Функции Matlab
Все М-файлы, с которыми работает система Matlab, делятся на две категории: скрипты и функции. Скрипт – это просто последовательность команд, в которой используются переменные из основного рабочего пространства Matlab. Функция – это подпрограмма, которая принимает аргументы (параметры) и возвращает результаты. В отличие от функций в большинстве языков программирования, функция Matlab может возвращать несколько результатов (а не один). Функция отличается от скрипта тем, что имеет заголовок, который начинается словом function. Например, заголовок
function [a,b,c,d] = qq ( x, y, z )
определяет функцию с именем qq, которая принимает три параметра (x, y и z) и возвращает 4 результата (a, b, c и d). В отличие от большинства современных языков, типы переменных (целая, вещественная, символьная, массив и т.д.) не определяются заранее, каждая из них содержать любые допустимые в Matlab данные.
Функция записывается в М-файл (с расширением .m), имя которого должно совпадать с именем функции. Например, функция qq должна быть записана в файл qq.m. Современные версии Matlab вообще не обращают внимание на имя функции (в заголовке), важно только имя файла.
Функция имеет своё пространство переменных и не может напрямую обращаться к переменным основного рабочего пространства. Внутри функции доступны аргументы, кроме того, можно вводить и использовать новые переменные. Для того, чтобы вернуть нужные значения, надо записать их в переменные a, b, c и d. Оператор return используется для досрочного возврата из функции (до этого во все выходные переменные должны быть записаны нужные значения).
Функции могут вызываться по имени из командной строки Matlab, из скрипта или из другой функции. Например, для вызова рассмотренной выше функции qq надо набрать команду вида
[w,e,r,t] = qq ( x1, 4*x2, 3 )
В данном случае при работе функции вместо x используется значение переменной x1, вместо y – значение выражения 4*x2, а вместо z – число 3. Результаты функции записываются в переменные w, e, r и t.
При вызове функции количество входных и выходных переменных может быть меньше (но не больше!), чем в заголовке функции. Внутри функции число входных параметров хранится в специальной переменной nargin, а число выходных величин – в переменной nargout.
Некоторые стандартные функции Matlab
Система Matlab включает большой набор стандартных функций. Большинство этих функций также оформлены в виде М-файлов, их адрес можно узнать с помощью команды which (см. работу № 1). В этой работе используются три функции:
abs – вычисление модуля числа или модуля каждого элемента массива
max – вычисление максимального значения в массиве (есть также функция min для вычисления минимального значения)
find – поиск элементов массива, соответствующих заданному условию.
Работа с функциями abs и max достаточно очевидна, поэтому рассмотрим только функцию find. Она возвращает индексы (номера) элементов массива, которые удовлетворяют заданному условию. Например, если A – массив, а b – число, по команда
>> ind = find ( A > b )
в переменную ind записывается массив номеров элементов массива A, которые больше b. В условии можно использовать знаки <, >, <=, >=, = = (равно), ~= (не равно). Сложные условия строятся с помощью операций ~ (НЕ), & (И) и | (ИЛИ) так же, как и в других языках программирования.
Программирование в среде Matlab Цели работы
освоение методов программирования в среде Matlab
Задачи работы
научиться передавать данные из рабочей области Matlab в модель Simulink
научиться составлять дополнительные функции Matlab
освоить некоторые способы автоматизации вычислений
Оформление отчета
Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать
название предмета, номер и название лабораторной работы
фамилию и инициалы авторов, номер группы
фамилию и инициалы преподавателя
номер варианта
краткое описание исследуемой системы
результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.
При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.
Описание системы
В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.
Структурная схема системы стабилизации судна на курсе
Линейная математическая модель, описывающая рыскание судна, имеет вид
где – угол рыскания (угол отклонения от заданного курса), – угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, – постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
.
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией24
,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией25
, где сек и сек.
Инструкция по выполнению работы
Этап выполнения задания |
Команды Matlab |
|
ЛКМ по кнопке справа от поля Current Directory |
|
View – Current directory |
|
двойной щелчок на lab4.mdl |
|
File – Save as ... |
|
|
|
Двойной щелчок на блоке Final value |
|
Судно, Numerator: K Denominator: [Ts 1 0] ПД-регулятор: Numerator: Kc*[Ts+1 1] И-канал, Denominator: [TI 0] Гирокомпас, Denominator: [Toc 1] Привод, Denominator: [TR 0] Ограничение скорости перекладки руля: ±TR*ddMax Ограничение угла перекладки руля: ±deltaMax |
|
|
|
|
|
File – New – M-file |
|
clear all; clc; K = 0.0694; Ts = 18.2; TR = 2; Toc = 6; ddMax = 3; deltaMax = 30; phiZad = 30; fConst = 0; TI = 200; Kc = 0.7045; |
|
клавиша F5 ЛКМ по кнопке |
|
двойной щелчок на lab4graph.m File – Save as... |
|
function lab5graph ( phi, delta ) |
|
|
|
title ( ... ) |
|
sysdata; sim ( 'lab5' ) lab5graph ( phi, delta ) |
1 function [sigma,Tpp] = overshoot ( t, y ) 2 yInf = y(end); 3 diff = (y - yInf) / abs (yInf); 4 sigma = max(diff) * 100; 5 i = find(abs(diff) > 0.02); 6 Tpp = t(max(i)+1); Комментарий: 1 – объявление функции overshoot, которая принимает два параметра-массива (время t и переходный процесс y) и возвращает два значения (перерегулирование в процентах sigma и время переходного процесса Tpp). 2 – вычисление последнего значения массива y, которое принимается за установившееся значение 3 – вычисление относительного отклонения в каждой точке графика 4 – вычисление перерегулирования в процентах 5 – в массив i записываются номера всех элементов массива diff, которые по модулю больше 0.02 (для определения времени переходного процесса используется отклонение 2%) 6 – вычисляется время переходного процесса как первый элемент массива t, после которого все элементы массива y отклоняются от установившегося значения не более, чем на 2%. |
|
|
|
|
|
1 Ts0 = Ts; 2 aTs = linspace(0.8, 1.2, 100) * Ts0; 3 aSi = []; aTpp = []; 4 for Ts=aTs 5 sim ( 'lab5' ) 6 [si,Tpp] = overshoot ( phi(:,1), phi(:,2) ); 7 aSi = [aSi si]; 8 aTpp = [aTpp Tpp]; 9 end; Комментарий: 1 – сохраняем номинальное значение постоянной времени в переменной Ts0 2 – создается массив из 100 постоянных времени, которые изменяются в диапазоне от 80 до 120% от номинального (расчетного) значения 3 – создаются пустые массивы aSi (для хранения значений перерегулирования) и aTpp (для хранения значений времени переходного процесса) 4 – начало цикла, переменная Ts принимает последовательно все значения из массива aTs 5 – моделирование при новом значении Ts 6 – вычисление перерегулирования и времени переходного процесса 7 – в конец массива aSi добавляется новое значение 8 – в конец массива aTpp добавляется новое значение 9 – конец цикла |
|
|
ПД-регулятор: Numerator: Kc*[Ts0+1 1] |
|
клавиша F5 |
|
|
|
выделить строки, клавиша F9 |
|
Simulation – Simulation parameters – Max step size = 0.2 |
|
|
|
|
|
|
Таблица коэффициентов
Вариант |
, сек |
, рад/сек |
, сек |
, сек |
|
|
16.0 |
0.06 |
1 |
1 |
|
|
16.2 |
0.07 |
2 |
2 |
|
|
16.4 |
0.08 |
1 |
3 |
|
|
16.6 |
0.07 |
2 |
4 |
|
|
16.8 |
0.06 |
1 |
5 |
|
|
17.0 |
0.07 |
2 |
6 |
|
|
17.2 |
0.08 |
1 |
1 |
|
|
17.4 |
0.07 |
2 |
2 |
|
|
17.6 |
0.06 |
1 |
3 |
|
|
17.8 |
0.07 |
2 |
4 |
|
|
18.0 |
0.08 |
1 |
5 |
|
|
18.2 |
0.09 |
2 |
6 |
|
|
18.4 |
0.10 |
1 |
1 |
|
|
18.6 |
0.09 |
2 |
2 |
|
|
18.8 |
0.08 |
1 |
3 |
|
|
19.0 |
0.07 |
2 |
4 |
|
|
19.2 |
0.08 |
1 |
5 |
|
|
19.4 |
0.09 |
2 |
6 |
|
|
19.6 |
0.10 |
1 |
1 |
|
|
18.2 |
0.0694 |
2 |
6 |
Контрольные вопросы к защите
См. все вопросы к работам № 1– 4.
В параметрах блока модели указано имя переменной. Как задать ее значение?
Как ввести ограничение на скорость перекладки руля, если известна постоянная времени привода?
Что такое М-файл?
Как создать новый М-файл?
Где выводятся сообщения об ошибках при выполнении скрипта или функции?
Как строится заголовок функции в М-файле?
Может ли функция возвращать несколько величин?
Можно ли обращаться к переменным рабочей области Matlab внутри функции?
Как вызывается функция, записанная в М-файл?
Как выделить последний элемент массива?
Чему равен результат операции A-x, где A – массив, а x – число?
Как работает функция find?
Как изменить функцию overshoot, чтобы она определяла время переходного процесса с точностью 5%?
Что такое грубость (робастность) системы?
Что означает запись
x = [];
x = [x y];
phi(:,1)
phi(1,:)
Как выполнить только несколько строк из скрипта?
Пример оформления отчета. Программирование в среде Matlab
1.Описание системы
Исследуется нелинейная система управления судном по курсу, структурная схема которой показана на рисунке.
Движение судна описывается линейной математической моделью в виде передаточной функции
, где рад/сек, сек,
Линейная модель привода представляет собой интегрирующее звено с передаточной функцией
, сек,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией
, сек,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией
,
где , сек, сек, сек,
Модификация нелинейной модели
подсистема «Судно»

подсистема «Привод»
пределы насыщения для блока «Saturation»,
ограничивающего скорость перекладки
руля, должны быть введены как
 ,
потому что …
,
потому что …
подсистема «Регулятор»

Функция для построения графиков переходных процессов
function lab5graph ( phi, delta )
figure(1);
subplot(2,1,1);
set(gca,'FontSize',16);
...
h = get(gca, 'Children');
set(h(1),'LineWidth',1.5)
Скрипт sysdata.m для загрузки исходных данных
clear all;
clc;
K = 0.0694;
Ts = 18.2;
...
phiZad = 30;
fConst = 0;
Скрипт lab5go.m для запуска модели
sysdata;
sim ( 'lab5' )
lab5graph ( phi, delta )
Функция overshoot
function [sigma,Tpp] = overshoot ( t, y )
yInf = y(end);
diff = (y - yInf) / abs (yInf);
sigma = max(diff) * 100;
i = find(abs(diff) > 0.02);
Tpp = t(max(i)+1);
Влияние постоянной времени судна на показатели качества
скрипт lab5go1.m для проведения расчетов
sysdata;
Ts0 = Ts;
aTs = linspace(0.8, 1.2, 100) * Ts0;
...
h = get(gca, 'Children');
set(h(1),'LineWidth',1.5)
графики изменения перерегулирования и времени переходного процесса

при увеличении постоянной времени перерегулирование … (как изменяется?)
время переходного процесса … (как изменяется?)
Влияние угла поворота на показатели качества
скрипт lab5go2.m для проведения расчетов
sysdata;
aPhi = linspace(1, 110, 180);
...
h = get(gca, 'Children');
set(h(1),'LineWidth',1.5)
графики изменения перерегулирования и времени переходного процесса
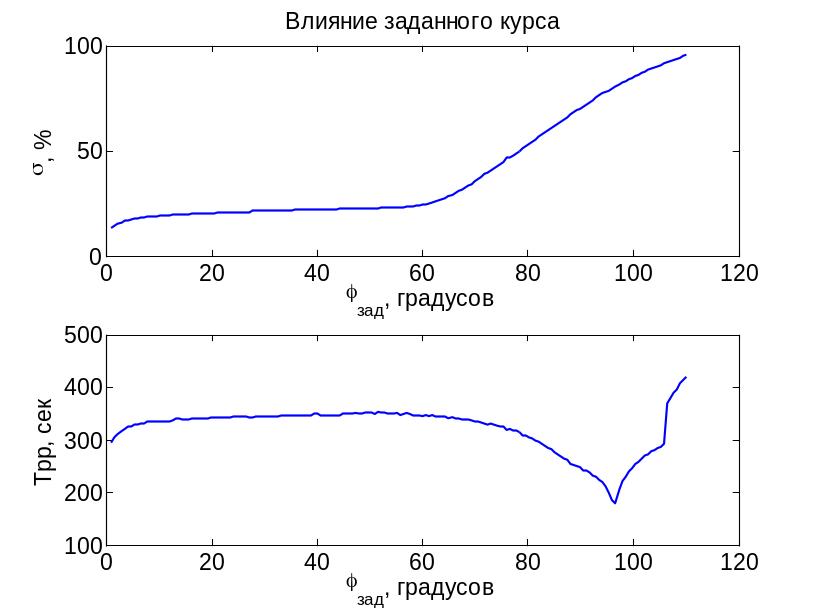
при увеличении угла поворота до
 перерегулирование … (как изменяется?),
время переходного процесса … (как
изменяется?)
перерегулирование … (как изменяется?),
время переходного процесса … (как
изменяется?)при углах поворота свыше перерегулирование … (как изменяется?), время переходного процесса … (как изменяется?); это объясняется тем, что …
при дальнейшем увеличении угла поворота … (что может быть?)
для линейной системы графики … (как должны выглядеть?)
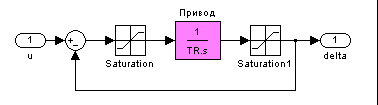
Самостоятельная работа студента с преподавателем № 6 (11, 12). Оптимизация нелинейных систем Эффект насыщения
В реальных системах всегда есть ограничения на максимальную величину управляющего воздействия. В судовых системах управления это, например, предельная скорость электромотора привода, предельное значение угла перекладки руля, предельная скорость перекладки. На малых углах поворота влиянием таких нелинейных ограничений можно пренебречь, однако при больших величинах сигналов они существенно изменяют свойства системы.
Нелинейности такого типа называются «насыщением»:


Они описываются уравнением
 ,
,
где
–
сигнал на входе звена,
–
сигнал на выходе (с учетом насыщения),
 и
и
 –
допустимые пределы.
–
допустимые пределы.
Для компенсации постоянных возмущений в регулятор часто вводится интегрирующее звено. При этом в системах с насыщением наблюдается эффект «залипания» интегратора. Он заключается в том, что управляющий сигнал уже достиг предельного значения, а интегратор продолжает интегрировать («наматывать», windup) ошибку, хотя увеличивать управление уже нельзя. Когда ошибка изменит знак, потребуется переложить руль в другую сторону, но этого не произойдет, поскольку выход интегратора очень велик. В результате увеличивается перерегулирование и время переходного процесса. На практике такое поведение системы может оказаться недопустимым.
Компенсация эффекта насыщения (anti-windup)
Для того, чтобы предотвратить «наматывание» интегратора, используются специальные приемы нелинейной коррекции. Они сводятся к одному из двух вариантов:
Условное интегрирование: если сигнал управления достигает предельного значения, интегратор отключается и интегрирование останавливается
Техника anti-windup: из входа интегратора вычитается сигнал, который поступает с блока компенсации насыщения. Именно этот вариант мы будем исследовать.
Пусть интегратор включается параллельно остальной части регулятора, т.е., имеет вид
 ,
,
где
 – часть регулятора, не содержащая
интегрирующих звеньев, а
– постоянная времени интегрирующего
звена.
– часть регулятора, не содержащая
интегрирующих звеньев, а
– постоянная времени интегрирующего
звена.

Блок компенсации насыщения генерирует сигнал
 ,
,
где – сигнал на выходе регулятора, а – сигнал с учетом насыщения:
,
причем пределы
и
выбираются такие же, как и допустимые
пределы для выходного сигнала привода.
Если сигнал
находится в допустимых пределах (в
интервале
 ),
то
),
то
 и система работает в линейном режиме,
без насыщения. Если же сигнал
выходит из диапазона
,
сигнал
и система работает в линейном режиме,
без насыщения. Если же сигнал
выходит из диапазона
,
сигнал
 ,
не равный нулю, подается через усилитель
на вход интегратора с обратным знаком,
противодействуя «накручиванию»
интегратора и возрастанию его выходного
сигнала.
,
не равный нулю, подается через усилитель
на вход интегратора с обратным знаком,
противодействуя «накручиванию»
интегратора и возрастанию его выходного
сигнала.
Заметим, что вместо усилителя с
коэффициентом
 можно устанавливать динамическое звено,
однако простейшего варианта часто
бывает достаточно.
можно устанавливать динамическое звено,
однако простейшего варианта часто
бывает достаточно.
Аналогичная идея может быть использована и в том случае, когда интегратор подключается последовательно, т.е.,
 ,
,
где – часть регулятора, не содержащая интегрирующих звеньев. Соответствующая блок-схема системы показана на рисунке.

Для того, чтобы выбрать коэффициент , можно использовать различные методы теории нелинейных систем или математическое моделирование. С инженерной точки зрения проще второй способ, который позволяет в интерактивном режиме методом проб и ошибок выбрать подходящее значение . В среде Matlab поиск можно автоматизировать с помощью пакета NCD Blockset (Nonlinear Control Design).
Пакет ncd Blockset
Пакет NCD Blockset (Nonlinear Control Design) предназначен для настройки параметров нелинейной модели методом численной оптимизации по переходному процессу.
С помощью ломаных линий задается область,
из которой не должен выходить переходный
процесс. Интервал, на котором выполняется
моделирование, разбивается на небольшие
участки шириной
 .
Для этих точек строится система
неравенств, которым должна удовлетворять
функция, описывающая переходный процесс.
На рисунке отрезками красного цвета
показано, где эти неравенства нарушены.
Требуется выбрать параметры модели
так, чтобы нарушений было как можно
меньше и величины отклонений были
минимальны. В идеале весь переходный
процесс вписывается в допустимую
область, нарушений вообще нет.
.
Для этих точек строится система
неравенств, которым должна удовлетворять
функция, описывающая переходный процесс.
На рисунке отрезками красного цвета
показано, где эти неравенства нарушены.
Требуется выбрать параметры модели
так, чтобы нарушений было как можно
меньше и величины отклонений были
минимальны. В идеале весь переходный
процесс вписывается в допустимую
область, нарушений вообще нет.
Для решения этой задачи в пакете NCD Blockset используются процедуры нелинейной оптимизации с ограничениями из пакета Optimization Toolbox.

Сначала надо перетащить в модель Simulink блок NCD Outport из группы NCD Blockset и подать на его вход сигнал, который надо «вписать» в заданную область. По умолчанию границы области устанавливаются так, чтобы установившееся значение сигнала было равно единице. Если это не так, на входе блока NCD Outport можно поставить дополнительный усилитель (блок Gain), который изменит масштаб. Например, если установившееся значение равно 10, коэффициент усиления надо сделать равным 0.1, чтобы установившееся значение на входе блока NCD Outport было равно 1.


Двойной щелчок по блоку NCD Outport открывает рабочее окно для подбора параметра.

Перетаскивая красные полоски вверх и вниз, можно менять границы допустимой области (она залита черным цветом). Можно также перетаскивать влево и вправо вертикальные границы. Щелчок ПКМ по красной полосе позволяет задать параметры ограничения более точно в диалоговом окне.
Для того, чтобы разбить полоску на две (сделать более точную границу) надо выделить ее щелчком мыши и щелкнуть по кнопке Split.
Чтобы задать параметры поиска, надо выбрать в этом окне пункт верхнего меню Optimization – Optimization Parameters:

В поле Tunable variables вводятся через пробел имена переменных, значения которых требуется подобрать. Поля Lower bounds (нижние границы значений переменных) и Upper bounds (верхние границы) необязательны для заполнения.
В поле Discretization interval надо ввести величину шага h (см. рисунок выше). От шага зависит количество интервалов и количество ограничений. Чем меньше шаг, тем больше задается ограничений и медленнее работает процедура поиска. С другой стороны, при очень большом шаге снижается точность. Рекомендуется выбирать этот параметр равным 1-2% от общего времени моделирования.
Перед запуском процедуры оптимизации надо ввести первое приближение для неизвестных параметров в командном окне Matlab:
Kaw = 0.2;
После этого следует щелкнуть по кнопке Start в окне блока NCD Outport. Информацию о ходе процесса и сообщения об ошибках можно наблюдать в командном окне Matlab. Обычно для того, чтобы добиться качественных переходных процессов, приходится несколько раз запускать процедуру оптимизации, меняя ограничения и последовательно улучшая результат.
Оптимизация нелинейных систем Цели работы
освоение методов оптимизации нелинейных систем в среде Matlab
Задачи работы
научиться копировать подсистемы из одной модели в другую
изучить приемы, позволяющие частично компенсировать нелинейность типа «насыщение» в системе с ПИД-регулятором
научиться использовать пакет NCD (Nonlinear Control Design)
Оформление отчета
Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать
название предмета, номер и название лабораторной работы
фамилию и инициалы авторов, номер группы
фамилию и инициалы преподавателя
номер варианта
краткое описание исследуемой системы
результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.
При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.
Описание системы
В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.

Структурная схема системы стабилизации судна на курсе
Линейная математическая модель, описывающая рыскание судна, имеет вид
где – угол рыскания (угол отклонения от заданного курса), – угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, – постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
.
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией28
,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией29
, где сек и сек.
Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используется схема с внутренней нелинейной обратной связью, охватывающей интегратор в составе регулятора.

Базовый регулятор, построенный по линейной модели, выделен серым фоном. Сигнал на его выходе представляет собой желаемый угол перекладки руля. Для блока нелинейной коррекции типа «насыщение» выбираются пределы, равные ограничениям на угол перекладки руля.
Если насыщения нет, разность сигналов
 равна нулю, и обратная связь не работает;
используется закон управления,
синтезированный для линейной системы.
Если сигнал
превышает допустимые пределы, разность
подается (со знаком «минус») на вход
интегратора через усилитель. Таким
образом, при насыщении сигнал на входе
интегратора ослабляется тем сильнее,
чем больше разность между желаемым и
допустимым углами перекладки. Такой
метод коррекции получил в литературе
название anti-windup
(противодействие «наматыванию»).
равна нулю, и обратная связь не работает;
используется закон управления,
синтезированный для линейной системы.
Если сигнал
превышает допустимые пределы, разность
подается (со знаком «минус») на вход
интегратора через усилитель. Таким
образом, при насыщении сигнал на входе
интегратора ослабляется тем сильнее,
чем больше разность между желаемым и
допустимым углами перекладки. Такой
метод коррекции получил в литературе
название anti-windup
(противодействие «наматыванию»).
В ходе выполнения работы для выбора оптимального значение коэффициента применяются процедуры численной оптимизации пакета NCD Blockset.
Инструкция по выполнению работы
Этап выполнения задания |
Команды Matlab |
|
ЛКМ по кнопке справа от поля Current Directory |
|
File – New – M-file File – Save клавиша F5 |
|
View – Current directory |
|
двойной щелчок на lab5.mdl |
|
File – Save as ... |
|
выделить ЛКМ, нажать Delete |
|
перетащить ПКМ |+- в поле List of signs |
|
перетащить ПКМ нажать Ctrl+I +-| в поле List of signs |
|
перетащить ЛКМ нажать Ctrl+I
|
|
Kaw в поле Gain |
|
|
|
Kaw = 1; |
|
|
|
открыть нужную модель, перетаскивание ЛКМ |
|
двойной щелчок ЛКМ 3 в поле Number of inputs |
|
|
|
sim ('lab6' ) figure(1) ... |
|
|
|
View – Library Browser перетаскивание ЛКМ двойной щелчок по блоку 1/phiZad в поле Gain |
|
|
|
|
|
|
|
|
|
ЛКМ по кнопке Start |
|
|
|
Kaw |
|
клавиша F5 |
|
[si,Tpp] = overshoot(phi(:,1),... phi(:,4)); |
|
в командном окне phiZad = 30; выделить нужные строки скрипта, нажать F9 |
|
|
Таблица коэффициентов
Вариант |
, сек |
, рад/сек |
, сек |
, сек |
|
|
16.0 |
0.06 |
1 |
1 |
|
|
16.2 |
0.07 |
2 |
2 |
|
|
16.4 |
0.08 |
1 |
3 |
|
|
16.6 |
0.07 |
2 |
4 |
|
|
16.8 |
0.06 |
1 |
5 |
|
|
17.0 |
0.07 |
2 |
6 |
|
|
17.2 |
0.08 |
1 |
1 |
|
|
17.4 |
0.07 |
2 |
2 |
|
|
17.6 |
0.06 |
1 |
3 |
|
|
17.8 |
0.07 |
2 |
4 |
|
|
18.0 |
0.08 |
1 |
5 |
|
|
18.2 |
0.09 |
2 |
6 |
|
|
18.4 |
0.10 |
1 |
1 |
|
|
18.6 |
0.09 |
2 |
2 |
|
|
18.8 |
0.08 |
1 |
3 |
|
|
19.0 |
0.07 |
2 |
4 |
|
|
19.2 |
0.08 |
1 |
5 |
|
|
19.4 |
0.09 |
2 |
6 |
|
|
19.6 |
0.10 |
1 |
1 |
|
|
18.2 |
0.0694 |
2 |
6 |
Контрольные вопросы к защите
См. все вопросы к работам № 1– 5.
Пусть линеаризованная система устойчива. Может ли система стать неустойчивой при учете насыщения привода? На каких режимах это особенно опасно?
Является ли примененный способ коррекции линейным или нелинейным? Почему?
Как работает регулятор, если сигналы не выходят за допустимые пределы? Почему (докажите по схеме)?
Что такое anti-windup?
Объясните действие блока Gain.
Как скопировать блок из одной модели в другую?
Как изменить число входов мультиплексора?
Зачем нужен нормирующий усилитель?
Как нужно подключать блок NCD Outport?
Как устанавливать ограничения на переходную функцию?
Как установить пределы для поиска решения в блоке NCD Outport?
Пример оформления отчета. Оптимизация нелинейных систем в среде Matlab
1.Описание системы
Исследуется нелинейная система управления судном по курсу, структурная схема которой показана на рисунке.
Движение судна описывается линейной математической моделью в виде передаточной функции
, где рад/сек, сек,
Линейная модель привода представляет собой интегрирующее звено с передаточной функцией
, сек,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией
, сек,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией
,
где , сек, сек, сек,
Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используется схема с нелинейной обратной связью, охватывающей интегратор в составе регулятора. В ходе работы требуется выбрать оптимальное значение коэффициента усиления в обратной связи с помощью пакета NCD Blockset.
2.Блок компенсации насыщения
подсистема «Регулятор»
пределы для блока Saturation

номинальное значения

модель для сравнения трех типов систем
переходные процессы при

при введении компенсации насыщения интегрирующего звена … (что наблюдается?)
3.Оптимальный выбор
модель для оптимизации
переходные процессы при
 (поворот на 90 градусов)
(поворот на 90 градусов)

перерегулирование
 ,
время переходного процесса
,
время переходного процесса
 сек.
сек.переходные процессы при повороте на 30 градусов
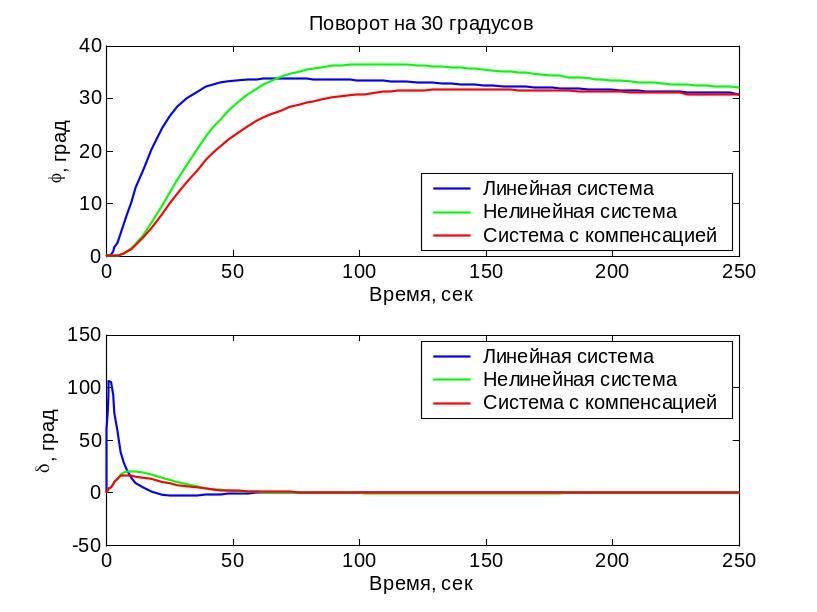
перерегулирование
 ,
время переходного процесса
,
время переходного процесса
 сек.
сек.применение оптимальной компенсации позволило … (сравнить с линейной и нелинейной системой)
Оптимизация нелинейных систем Цели работы
освоение методов оптимизации нелинейных систем в среде Matlab
Задачи работы
научиться копировать подсистемы из одной модели в другую
изучить приемы, позволяющие частично компенсировать нелинейность типа «насыщение» в системе с ПИД-регулятором
научиться использовать пакет NCD (Nonlinear Control Design)
Оформление отчета
Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать
название предмета, номер и название лабораторной работы
фамилию и инициалы авторов, номер группы
фамилию и инициалы преподавателя
номер варианта
краткое описание исследуемой системы
результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.
При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.
Описание системы
В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.
Структурная схема системы стабилизации судна на курсе
Линейная математическая модель, описывающая рыскание судна, имеет вид
где – угол рыскания (угол отклонения от заданного курса), – угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, – постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
.
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией30
,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией31
, где сек и сек.
Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используется схема с внутренней нелинейной обратной связью, охватывающей интегратор в составе регулятора.
Базовый регулятор, построенный по линейной модели, выделен серым фоном. Сигнал на его выходе представляет собой желаемый угол перекладки руля. Для блока нелинейной коррекции типа «насыщение» выбираются пределы, равные ограничениям на угол перекладки руля.
Если насыщения нет, разность сигналов равна нулю, и обратная связь не работает; используется закон управления, синтезированный для линейной системы. Если сигнал превышает допустимые пределы, разность подается (со знаком «минус») на вход интегратора через усилитель. Таким образом, при насыщении сигнал на входе интегратора ослабляется тем сильнее, чем больше разность между желаемым и допустимым углами перекладки. Такой метод коррекции получил в литературе название anti-windup (противодействие «наматыванию»).
В ходе выполнения работы для выбора оптимального значение коэффициента применяются процедуры численной оптимизации пакета NCD Blockset.
Инструкция по выполнению работы
Этап выполнения задания |
Команды Matlab |
|
ЛКМ по кнопке справа от поля Current Directory |
|
File – New – M-file File – Save клавиша F5 |
|
View – Current directory |
|
двойной щелчок на lab5.mdl |
|
File – Save as ... |
|
выделить ЛКМ, нажать Delete |
|
перетащить ПКМ |+- в поле List of signs |
|
перетащить ПКМ нажать Ctrl+I +-| в поле List of signs |
|
перетащить ЛКМ нажать Ctrl+I
|
|
Kaw в поле Gain |
|
|
|
Kaw = 1; |
|
|
|
открыть нужную модель, перетаскивание ЛКМ |
|
двойной щелчок ЛКМ 3 в поле Number of inputs |
|
|
|
sim ('lab6' ) figure(1) ... |
|
|
|
View – Library Browser перетаскивание ЛКМ двойной щелчок по блоку 1/phiZad в поле Gain |
|
|
|
|
|
|
|
|
|
ЛКМ по кнопке Start |
|
|
|
Kaw |
|
клавиша F5 |
|
[si,Tpp] = overshoot(phi(:,1),... phi(:,4)); |
|
в командном окне phiZad = 30; выделить нужные строки скрипта, нажать F9 |
|
|
Таблица коэффициентов
Вариант |
, сек |
, рад/сек |
, сек |
, сек |
|
|
16.0 |
0.06 |
1 |
1 |
|
|
16.2 |
0.07 |
2 |
2 |
|
|
16.4 |
0.08 |
1 |
3 |
|
|
16.6 |
0.07 |
2 |
4 |
|
|
16.8 |
0.06 |
1 |
5 |
|
|
17.0 |
0.07 |
2 |
6 |
|
|
17.2 |
0.08 |
1 |
1 |
|
|
17.4 |
0.07 |
2 |
2 |
|
|
17.6 |
0.06 |
1 |
3 |
|
|
17.8 |
0.07 |
2 |
4 |
|
|
18.0 |
0.08 |
1 |
5 |
|
|
18.2 |
0.09 |
2 |
6 |
|
|
18.4 |
0.10 |
1 |
1 |
|
|
18.6 |
0.09 |
2 |
2 |
|
|
18.8 |
0.08 |
1 |
3 |
|
|
19.0 |
0.07 |
2 |
4 |
|
|
19.2 |
0.08 |
1 |
5 |
|
|
19.4 |
0.09 |
2 |
6 |
|
|
19.6 |
0.10 |
1 |
1 |
|
|
18.2 |
0.0694 |
2 |
6 |
Контрольные вопросы к защите
См. все вопросы к работам № 1– 5.
Пусть линеаризованная система устойчива. Может ли система стать неустойчивой при учете насыщения привода? На каких режимах это особенно опасно?
Является ли примененный способ коррекции линейным или нелинейным? Почему?
Как работает регулятор, если сигналы не выходят за допустимые пределы? Почему (докажите по схеме)?
Что такое anti-windup?
Объясните действие блока Gain.
Как скопировать блок из одной модели в другую?
Как изменить число входов мультиплексора?
Зачем нужен нормирующий усилитель?
Как нужно подключать блок NCD Outport?
Как устанавливать ограничения на переходную функцию?
Как установить пределы для поиска решения в блоке NCD Outport?
Пример оформления отчета. Оптимизация нелинейных систем в среде Matlab
1.Описание системы
Исследуется нелинейная система управления судном по курсу, структурная схема которой показана на рисунке.
Движение судна описывается линейной математической моделью в виде передаточной функции
, где рад/сек, сек,
Линейная модель привода представляет собой интегрирующее звено с передаточной функцией
, сек,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией
, сек,
В качестве управляющего устройства используется ПИД-регулятор с передаточной функцией
,
где , сек, сек, сек,
Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используется схема с нелинейной обратной связью, охватывающей интегратор в составе регулятора. В ходе работы требуется выбрать оптимальное значение коэффициента усиления в обратной связи с помощью пакета NCD Blockset.
2.Блок компенсации насыщения
подсистема «Регулятор»
пределы для блока Saturation
номинальное значения
модель для сравнения трех типов систем
переходные процессы при
при введении компенсации насыщения интегрирующего звена … (что наблюдается?)
3.Оптимальный выбор
модель для оптимизации
переходные процессы при (поворот на 90 градусов)
перерегулирование , время переходного процесса сек.
переходные процессы при повороте на 30 градусов
перерегулирование , время переходного процесса сек.
применение оптимальной компенсации позволило … (сравнить с линейной и нелинейной системой)
Самостоятельная работа студента с преподавателем №7 (13, 14, 15 недели) Переоборудование непрерывного регулятора Задача переоборудования
Классические методы синтеза позволяют построить непрерывный регулятор, который описывается передаточной функцией или соответствующим дифференциальным уравнением. Для непосредственной реализации такого регулятора можно использовать различные аналоговые элементы, в том числе и электронные (RC-цепочки, операционные усилители и т.п.).
В то же время в современных системах управления законы регулирования чаще всего реализуются с помощью бортового цифрового компьютера или микроконтроллера. При этом
отсутствует дрейф параметров элементов регулятора (их изменение со временем, при изменении давления, температуры и т.п.);
компьютер позволяет реализовывать достаточно сложные алгоритмы управления, в том числе и адаптивные, что крайне трудно сделать на базе аналоговой техники;
для перестройки алгоритма управления не требуется менять аппаратуру, а надо просто заменить программу обработки данных.
Цифровые вычислительные устройства представляют собой элементы дискретного действия. Они периодически выполняют измерения входного сигнала и расчет нового управляющего воздействия. Период, через который эти операции повторяются, называется интервалом квантования и обозначается через .
На цифровых компьютерах нельзя напрямую реализовать управляющее устройство, которое описывается дифференциальным уравнением в непрерывном времени. Задача переоборудования состоит в том, чтобы заменить спроектированный непрерывный регулятор цифровым устройством так, чтобы сохранить все существенные свойства непрерывной системы (устойчивость, качество, подавление постоянных возмущений).
Компьютер в контуре управления
Компьютер в контуре управления можно представить в виде последовательное соединение трех звеньев:
импульсного элемента, который выбирает из непрерывного сигнала ошибки
 значения
значения
 в моменты квантования
в моменты квантования
 (при целых
);
импульсный элемент моделирует
аналого-цифровой преобразователь
(АЦП);
(при целых
);
импульсный элемент моделирует
аналого-цифровой преобразователь
(АЦП);линейного цифрового фильтра, который преобразует дискретную последовательность
 в управляющую последовательность
в управляющую последовательность
 ;
свойства этого фильтра определяют
закон управления;
;
свойства этого фильтра определяют
закон управления;восстанавливающее устройство (экстраполятор), которое восстанавливает непрерывный сигнал управления из последовательности ; экстраполятор моделирует цифро-аналоговый преобразователь (ЦАП), чаще всего используется фиксатор нулевого порядка, который удерживает постоянное значение в течение очередного интервала квантования:
 .
.
Схема цифрового регулятора показана на рисунке:

Блок ИЭ обозначает импульсный элемент (АЦП), блок ЦФ – цифровой фильтр, блок Э – экстраполятор (ЦАП). Точечные линии обозначают дискретные сигналы, сплошные линии – непрерывные сигналы.
Экстраполятор
Экстраполятором называют устройство,
которое восстанавливает непрерывный
сигнал управления
по
дискретной последовательности значений
 ,
поступающих с выхода цифрового фильтра
в моменты времени
.
Обычно вычислительное запаздывание
(время, необходимое на расчет очередного
значения
,
поступающих с выхода цифрового фильтра
в моменты времени
.
Обычно вычислительное запаздывание
(время, необходимое на расчет очередного
значения
 )
включают в модель объекта управления,
поэтому считается, что цифровой фильтр
выполняет обработку данных мгновенно.
)
включают в модель объекта управления,
поэтому считается, что цифровой фильтр
выполняет обработку данных мгновенно.
В простейшем случае ЦАП, получив новый
управляющий сигнал
от цифрового фильтра, просто удерживает
(фиксирует) его в течение интервала
квантования
![]() (до получения следующего значения
(до получения следующего значения
 ).
Такой экстраполятор называется фиксатором
нулевого порядка (англ. zero-order
hold, ZOH).
).
Такой экстраполятор называется фиксатором
нулевого порядка (англ. zero-order
hold, ZOH).

Фиксатор нулевого порядка
Фиксатор нулевого порядка восстанавливает сигнал по правилу
.
Здесь
 – так называемое локальное время,
прошедшее с момента последнего
срабатывания импульсного элемента.
– так называемое локальное время,
прошедшее с момента последнего
срабатывания импульсного элемента.
Предположим, что дискретная
последовательность получена в результате
квантования некоторого непрерывного
сигнала. Восстановленный сигнал будет
представлять собой «ступеньки», высота
которых совпадает с истинным значением
сигнала в начале интервала. Если провести
линию через середины этих «ступенек»,
получается сигнал, смещенный относительно
исходного на
![]() .
Поэтому говорят, что последовательно
примененные операции квантования и
восстановления сигнала с помощью
фиксатора нулевого порядка приводят к
его запаздыванию на половину периода.
.
Поэтому говорят, что последовательно
примененные операции квантования и
восстановления сигнала с помощью
фиксатора нулевого порядка приводят к
его запаздыванию на половину периода.
Существуют и более сложные экстраполяторы, учитывающие несколько последних значений последовательности , но они используются на практике крайне редко из-за проблем в реализации.
Цифровые фильтры
Цифровой фильтр – это устройство, преобразующее входную дискретную последовательность

в выходную

В реальных фильтрах для расчета очередного
значения управляющей последовательности
в момент времени
 используется конечное число прошлых
значений входного и выходного сигналов,
хранящихся в оперативной памяти:
используется конечное число прошлых
значений входного и выходного сигналов,
хранящихся в оперативной памяти:

Здесь
 –
некоторая функция своих переменных и
–
некоторая функция своих переменных и
 – целое число, называемое порядком
фильтра. Чаще всего используют линейные
законы управления, которые описываются
формулой
– целое число, называемое порядком
фильтра. Чаще всего используют линейные
законы управления, которые описываются
формулой
 ,
,
где
 и
и
 – вещественные числа. Уравнение такого
вида называют линейным разностным
уравнением регулятора. Оно аналогично
дифференциальному уравнению непрерывной
системы, но входной и выходной сигналы
изменяются в дискретном времени, т.е.,
определены только в моменты времени
.
– вещественные числа. Уравнение такого
вида называют линейным разностным
уравнением регулятора. Оно аналогично
дифференциальному уравнению непрерывной
системы, но входной и выходной сигналы
изменяются в дискретном времени, т.е.,
определены только в моменты времени
.
Как и для линейных непрерывных систем, для описания линейных цифровых фильтров (линейных дискретных систем) можно использовать операторный метод. В литературе чаще всего используется оператор сдвига вперед
 ,
,
 .
.
Обозначив через
 обратный
оператор, получим
обратный
оператор, получим
 и
и
 .
Тогда, перенося в левую часть все члены,
зависящие от выходной последовательности,
можно записать уравнение регулятора в
операторной форме
.
Тогда, перенося в левую часть все члены,
зависящие от выходной последовательности,
можно записать уравнение регулятора в
операторной форме
 .
.
Отношение

называется дискретной передаточной
функцией цифрового фильтра. Таким
образом, в операторной форме получаем
 .
.
Фактически задача переоборудования
сводится к тому, чтобы заменить
передаточную функцию
 непрерывного регулятора дискретной
передаточной функцией цифрового фильтра
непрерывного регулятора дискретной
передаточной функцией цифрового фильтра
 так, чтобы сохранить все существенные
свойства системы.
так, чтобы сохранить все существенные
свойства системы.
Методы численного интегрирования
Простейшие методы переоборудования
основаны на приближенной замене
интегрирующего звена с передаточной
функцией
 его дискретной моделью. Это позволяет
получить дискретную передаточную
функцию цифрового регулятора, сделав
соответствующую замену в передаточной
функции непрерывного регулятора
.
его дискретной моделью. Это позволяет
получить дискретную передаточную
функцию цифрового регулятора, сделав
соответствующую замену в передаточной
функции непрерывного регулятора
.
|
Непрерывный и дискретный интеграторы |
Пусть
 и
—
входной и выходной сигнал непрерывного
интегратора. Если известно значение
и
—
входной и выходной сигнал непрерывного
интегратора. Если известно значение
 ,
то
,
то
 .
.
Такое звено приближенно заменяется дискретным интегратором, для которого
 ,
,
где — некоторое правило построения следующего значения выхода по предыдущим значениям входа и выхода. Для решения этой задачи можно использовать любой метод численного интегрирования. Мы рассмотрим методы прямоугольников и трапеций.
|
Метод Эйлера (а) и метод обратных разностей (б) |
При использовании метода Эйлера имеем
 .
.
Используя оператор (сдвиг вперед), получаем


 .
.
Таким образом, переоборудование по методу Эйлера сводится к замене
 .
.
Аналогично можно построить правило замены для метода обратных разностей:
 .
.
Из курса численных методов известно, что методы прямоугольников дают низкую точность. Более совершенен метод трапеций:
 .
.
|
Метод трапеций |
Формула интегрирования по методу трапеций приводит к замене
 ,
,
которая называется преобразованием Тастина (или Тустена).
Для повышения точности аппроксимации можно использовать более сложные методы, например, замены
 ,
,
 ,
,
соответствующие методам интегрирования Симпсона и Уэддля. Их главный недостаток состоит в том, что порядок переоборудованного регулятора будет выше, чем порядок непрерывного.
Переоборудование пид-регулятора
Рассмотрим непрерывный ПД-регулятор с передаточной функцией
 .
.
Дискретизация с помощью методов Эйлера, обратных разностей и Тастина дает дискретные регуляторы вида
 ,
,
где коэффициенты равны
метод Эйлера
 ,
,
 ,
,
 ,
,
 .
.
метод обратных разностей
 ,
,
 ,
,
 ,
,
 .
.
преобразование Тастина
 ,
,
 ,
,
 ,
,
 .
.
Все регуляторы имеют тот же самый порядок (равный 1), что и непрерывный регулятор. Полученные дискретные регуляторы только приближенно заменяют непрерывный, фактически они всегда будут работать несколько хуже, чем .
ПД-регулятор будем переоборудовать с помощью преобразования Тастина (интегрирования методом трапеций), которое является наиболее точным из этих методов. В системе Matlab для этого можно использовать функцию c2d из пакета Control Toolbox:
>> Dpd = c2d ( Cpd, T, 'tustin' )
Здесь Cpd – модель (например, передаточная функция) непрерывного ПД-регулятора, T –интервал квантования.
Теперь рассмотрим интегральный канал:
 .
.
Используя рассмотренные выше методы переоборудования, получаем
метод Эйлера  ,
,
метод обратных разностей  ,
,
преобразование Тастина  .
.
Как будет показано дальше, для переоборудования интегрального канала лучше использовать преобразование Эйлера.
Ниже показана схема цифрового регулятора с компенсацией насыщения:

Здесь сплошные линии обозначают непрерывные сигналы, а штриховые – дискретные (числовые последовательности). ИЭ обозначает импульсный элемент (АЦП), а блок Э – экстраполятор (ЦАП).
Алгебраические циклы
Пусть интегральный канал переоборудован по методу обратных разностей
,
что соответствует разностному уравнению
 . (*)
. (*)
Теперь построим выражение для сигнала .
Учтем, что
.
Учтем, что
 и
и
 ,
,
где функция
 задает нелинейность типа «насыщение»:
задает нелинейность типа «насыщение»:

Объединяя эти формулы, получим разностное
уравнение для вычисления
 :
:
 .
.
В этой формуле значение , которое требуется рассчитать, входит и в правую часть! Это значит, что для вычисления требуется не просто подставить в формулу известные значения, а решить нелинейное уравнение относительно . Такое явление называется алгебраическим циклом, его желательно избегать. Более того, в сложных случаях это уравнение может не иметь решения вообще. Система Matlab-Simulink выдает предупреждение в случае обнаружения алгебраического цикла (algebraic loop) при моделировании.
Для того, чтобы не было алгебраического
цикла, правая часть разностного уравнения
(аналогичного уравнению (*)) не должна
зависеть от
.
Это будет в том случае, если передаточная
функция
 – строго правильная, т.е., степень ее
числителя меньше степени знаменателя.
Из всех рассмотренных вариантов
переоборудования интегратора этому
условию удовлетворяет метод Эйлера,
который мы и будем использовать в работе.
При попытке применить метод обратных
разностей или преобразование Тастина
возникает алгебраический цикл, потому
что степени числителя и знаменателя
передаточной функции
равны.
– строго правильная, т.е., степень ее
числителя меньше степени знаменателя.
Из всех рассмотренных вариантов
переоборудования интегратора этому
условию удовлетворяет метод Эйлера,
который мы и будем использовать в работе.
При попытке применить метод обратных
разностей или преобразование Тастина
возникает алгебраический цикл, потому
что степени числителя и знаменателя
передаточной функции
равны.
Цифровая реализация непрерывного регулятора Цели работы
освоение методов переоборудования непрерывных регуляторов для реализации на цифровом компьютере
Задачи работы
познакомиться с методами переоборудования непрерывных регуляторов в Matlab
научиться моделировать системы с цифровыми регуляторами
научиться выбирать интервал квантования
Оформление отчета
Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать
название предмета, номер и название лабораторной работы
фамилию и инициалы авторов, номер группы
фамилию и инициалы преподавателя
номер варианта
краткое описание исследуемой системы
результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.
При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.
Описание системы
В работе рассматривается система управления судном по курсу. Ее структурная схема показана на рисунке.

Структурная схема системы стабилизации судна на курсе
Линейная математическая модель, описывающая рыскание судна, имеет вид
где – угол рыскания (угол отклонения от заданного курса), – угловая скорость вращения вокруг вертикальной оси, – угол поворота вертикального руля относительно положения равновесия, – постоянная времени, – постоянный коэффициент, имеющий размерность рад/сек. Передаточная функция от угла поворота руля к углу рыскания запишется в виде
.
Линейная модель привода (рулевой машины) представляет собой интегрирующее звено с передаточной функцией
,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Для измерения угла рыскания используется гирокомпас, математическая модель которого записывается в виде апериодического звена первого порядка с передаточной функцией32
,
В непрерывной системе в качестве управляющего устройства используется ПИД-регулятор с передаточной функцией33
, где сек и сек.
Для компенсации эффекта насыщения, вызванного ограниченным углом перекладки руля, используется схема с внутренней нелинейной обратной связью, охватывающей интегратор в составе регулятора34.

Для реализации регулятора используется цифровой компьютер с интервалом квантования . Регулятор в расчетной схеме заменяется не последовательное соединение трех звеньев:
импульсного элемента, который выбирает из непрерывного сигнала значения в моменты квантования (при целых ); импульсный элемент моделирует аналого-цифровой преобразователь (АЦП);
линейного цифрового фильтра, который преобразует дискретную последовательность в управляющую последовательность ; передаточная функция этого фильтра определяет закон управления;
восстанавливающее устройство (экстраполятор), которое восстанавливает непрерывный сигнал управления из последовательности ; экстраполятор моделирует цифро-аналоговый преобразователь (ЦАП), чаще всего используется фиксатор нулевого порядка, который удерживает постоянное значение в течение очередного интервала квантования:
.
Схема цифрового регулятора показана на рисунке:

Блок ИЭ обозначает импульсный элемент (АЦП), блок Э – экстраполятор (ЦАП). Точечные линии обозначают дискретные сигналы, сплошные линии – непрерывные.
Цифровые регуляторы обладают многими преимуществами в сравнении с классическими (непрерывными):
отсутствует дрейф параметров элементов
в цифровой форме можно реализовать сложные законы управления
цифровые регуляторы легко перестраивать, настройка сводится к просто к замене алгоритма обработки измеряемых сигналов
В то же время между моментами квантования (моментами съема измеряемых сигналов и выдачи нового управляющего воздействия) система ведет себя как разомкнутая (неуправляемая). Это может привести к потере устойчивости (при больших интервалах квантования в сравнении с постоянной времени объекта) и скрытым колебаниям (колебаниям непрерывного сигнала, которые не проявляются в моменты квантования).
Для построения дискретной модели ПД-регулятора используется преобразование Тастина
 ,
,
соответствующее интегрированию по методу трапеций. Для рассматриваемого ПД-регулятора такая замена дает
,
где коэффициенты равны
,
,
 ,
,
 .
.
Для построения дискретной передаточной функции интегрального канала применяется метод интегрирования Эйлера (метод прямоугольников), т.е., замена
 .
.
В ходе выполнения работы требуется построить цифровые реализации регулятора при различных интервалах квантования и сравнить переходные процессы в непрерывной и цифровой системе управления.
Инструкция по выполнению работы
Этап выполнения задания |
Команды Matlab |
|
ЛКМ по кнопке справа от поля Current Directory |
|
File – New – M-file sysdata; Kaw = ... File – Save
|
1 T = 1; 2 Cpd = tf(Kc*[Ts+1 1], [1 1]); 3 Dpd = c2d ( Cpd, T, 'tustin' ); 4 [nD,dD] = tfdata ( Dpd, 'v' ); Комментарий: 1 – установить значение интервала квантования 1 с; 2 – построение передаточной функции ПД-регулятора; 3 – применение преобразования Тастина к передаточной функции Cpd; в результате будет построения соответствующая дискретная передаточная функция; 4 – числитель и знаменатель дискретной передаточной функции Dpd записываются в переменные nD и dD. |
|
|
клавиша F5 |
|
View – Current directory |
|
двойной щелчок на lab6.mdl |
|
File – Save as ... |
|
выделить ЛКМ, нажать Delete |
|
двойной щелчок 2 в поле Number of inputs |
|
перетащить ПКМ ЛКМ на названии |
|
ПКМ – Background color
|
|
ЛКМ выделить ЛКМ, нажать Delete |
|
View – Library browser перетащить ЛКМ |
|
ПД-регулятор Numerator: nD Denominator: dD Sample time: T Интегратор Numerator: [T] Denominator: TI*[1 -1] Sample time: T |
|
перетащить ЛКМ из окна Library browser Sample time: T |
|
|
|
Simulation – Simulation parameters – Stop time |
|
двойной щелчок ЛКМ по блокам Курс и Руль |
1 close all; 2 figure(1); 3 subplot(2,1,1); 4 set(gca,'FontSize',16); 5 subplot(2,1,2); 6 set(gca,'FontSize',16); Комментарий: 1 – закрыть все рисунки; 2 – создать рисунок номер 1; 3 – разбить его на две части по вертикали (курс и угол перекладки руля) и активизировать первый график; 4 – установить размер шрифта 16 пунктов; 5, 6 – те же операции для второго графика. |
|
1 aT = [2 3 5]; 2 col = 'bgr'; 3 for i=1:length(aT) 4 T = aT(i); 5 Dpd = c2d ( Cpd, T, 'tustin' ); 6 [nD,dD] = tfdata ( Dpd, 'v' ); 7 sim('lab7') 8 subplot(2,1,1); 9 plot(phi(:,1),phi(:,3),col(i)); 10 hold on; 11 subplot(2,1,2); 12 plot(delta(:,1),delta(:,3),col(i)); 13 hold on; 14 end; Комментарий: 1 – создается массив интервалов квантования; 2 – создается символьный массив с обозначениями цветов графиков ('b' – синий, 'g' – зеленый, 'r' – красный); 3 – заголовок цикла, i – номер графика; 4 – выбрать значение интервала квантования из массива; 5 – построить дискретную модель ПД-регулятора с помощью преобразования Тастина; 6 – получить числитель и знаменатель этой модели; 7 – выполнить моделирование; 8 – перейти к первому графику; 9 – построить изменение угла курса, цвет линии определяется символом из массива col; 10 – при выводе следующего графика не стирать существующие кривые; 11-13 – те же операции для второго графика (угол перекладки руля); 14 – конец цикла |
|
1 subplot(2,1,1); 2 plot(phi(:,1),phi(:,2),'k--'); 3 legend('T=2', 'T=3', 'T=5', 'Непрерывная система'); 4 h = get(gca, 'Children'); 5 for i=1:4 6 set(h(i),'LineWidth',1.5); 7 end; Комментарий: 1 – перейти к первому графику; 2 – строится переходный процесс в непрерывной системе, штриховая линия ('--') черного цвета ('k'); 3 – выводится легенда; 4 – получить массив указателей на линии; 5-7 – цикл для изменения толщины линий 6 – установить толщину линий 1,5; |
|
|
|
|
клавиша F5 |
|
print –dmeta ПКМ - Вставить |
|
|
Таблица коэффициентов
Вариант |
, сек |
, рад/сек |
, сек |
, сек |
|
|
16.0 |
0.06 |
1 |
1 |
|
|
16.2 |
0.07 |
2 |
2 |
|
|
16.4 |
0.08 |
1 |
3 |
|
|
16.6 |
0.07 |
2 |
4 |
|
|
16.8 |
0.06 |
1 |
5 |
|
|
17.0 |
0.07 |
2 |
6 |
|
|
17.2 |
0.08 |
1 |
1 |
|
|
17.4 |
0.07 |
2 |
2 |
|
|
17.6 |
0.06 |
1 |
3 |
|
|
17.8 |
0.07 |
2 |
4 |
|
|
18.0 |
0.08 |
1 |
5 |
|
|
18.2 |
0.09 |
2 |
6 |
|
|
18.4 |
0.10 |
1 |
1 |
|
|
18.6 |
0.09 |
2 |
2 |
|
|
18.8 |
0.08 |
1 |
3 |
|
|
19.0 |
0.07 |
2 |
4 |
|
|
19.2 |
0.08 |
1 |
5 |
|
|
19.4 |
0.09 |
2 |
6 |
|
|
19.6 |
0.10 |
1 |
1 |
|
|
18.2 |
0.0694 |
2 |
6 |
Контрольные вопросы к защите
См. все вопросы к работам № 1–6.
Что такое переоборудование?
В чем отличие непрерывной и цифровой систем управления?
В чем преимущества цифровых систем управления?
Что такое аналоговые и дискретные сигналы?
Что такое дискретная передаточная функция?
Что такое импульсный элемент? Моделью какого реального устройства он служит?
Что такое экстраполятор? Моделью какого реального устройства он служит?
Что такое фиксатор нулевого порядка? Почему более сложные экстраполяторы применяются редко?
Что такое цифровой фильтр?
Какой оператор используется для построения дискретной передаточной функции цифрового фильтра?
Как найти дискретную передаточную функцию фильтра, заданного разностным уравнением?
Какие методы переоборудования вы знаете? Какой из них наиболее точный?
Как выполнить переоборудование методом Эйлера?
Какая функция Matlab выполняет преобразование Тастина? Как ее вызывать?
В чем недостаток методов переоборудования на основе формул численного интегрирования Симпсона и Уэддля?
Почему для переоборудования ПД-регулятора использовано преобразование Тастина, а для интегральной части – метод Эйлера?
Что такое алгебраический цикл? В каком случае алгебраических циклов не возникает?
Какие эффекты наблюдаются при увеличении интервала квантования?
Как обосновать выбор интервала квантования при переоборудовании непрерывного регулятора?
Пример оформления отчета. Цифровая реализация непрерывного регулятора
1.Описание системы
Исследуется нелинейная система управления судном по курсу, структурная схема которой показана на рисунке.
Движение судна описывается линейной математической моделью в виде передаточной функции
, где рад/сек, сек,
Линейная модель привода представляет собой интегрирующее звено с передаточной функцией
, сек,
охваченное единичной отрицательной обратной связью. На угол перекладки руля и скорость перекладки накладываются нелинейные ограничения
, .
Измерительное устройство (гирокомпас) моделируется как апериодическое звено с передаточной функцией
, сек,
В непрерывной системе в качестве управляющего устройства используется ПИД-регулятор с передаточной функцией
,
где , сек, сек, сек,
2.Переоборудование непрерывного регулятора
Для построения дискретной модели ПД-регулятора используется преобразование Тастина
,
соответствующее интегрированию по методу трапеций. Для рассматриваемого ПД-регулятора получаем

 ,
,
где коэффициенты равны
 ,
,
 ,
,
 ,
,
 .
.
Для построения дискретной передаточной функции интегрального канала применяется метод интегрирования Эйлера (метод прямоугольников), т.е., замена
,
что дает
.
При заданных численных значениях и
 получаем
получаем
 ,
,
 .
.
3.Подсистема «Регулятор» в цифровой системе
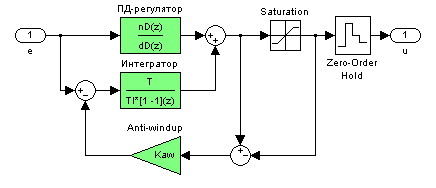
пределы для блока Saturation
коэффициент компенсации насыщения

модель для сравнения трех типов систем
4.Выбор интервала квантования
переходные процессы при


для данной системы рекомендуется выбирать интервал квантования не более …
1 Черным цветом обозначается ввод пользователя, синим – ответ среды Matlab.
2 В зарубежной литературе для одномерных систем используется сокращение SISO = Single Input Single Output.
3 Полюса передаточной функции являются собственными числами матрицы . Таким образом, если у передаточной функции есть полюс в точке , матрица будет вырожденной.
4 Для нелинейных систем это неверно.
5 Значение возвращается функцией damp как собственная частота для вещественного полюса.
6 Все коэффициенты надо взять из таблицы в конце файла.
7 По умолчанию в Matlab время переходного процесса определяется для 2%-ного отклонения от установившегося значения.
8 Точка с запятой в конце команды подавляет вывод на экран результата выполнения. Это удобно при работе с большими массивами.
9 Частотная характеристика возвращается в виде трехмерного массива, в котором каждый элемент имеет 3 индекса: строка, столбец (для многомерных моделей) и номер точки частотной характеристики. Для системы с одним входом и одним выходом команда r = r(:); преобразует эти данные в в обычный одномерный массив.
10 Этим термином также называется совокупность траекторий, которые описывают корни характеристического уравнения при изменении любого числового коэффициента в системе.
11 Численные значения , , и надо взять из таблицы в конце файла.
12 В зарубежной литературе ЛАФЧХ называют диаграммой Боде.
13 SISO = Single Input Single Output, система с одним входом и выходом.
14 LTI = Linear Time-Invariant, линейная стационарная система.
15 По умолчанию в Matlab время переходного процесса определяется для 2%-ного отклонения от установившегося значения.
16 В некоторых версиях Matlab существуют проблемы с русской буквой «Я», поэтому рекомендуется использовать английские названия блоков.
17 ТеХ – лучшая в мире система подготовки текстов с математическими формулами, разработанная математиком и программистом Дональдом Кнутом (автором многотомного издания «Искусство программирования для ЭВМ»). Чаще всего используются так называемые макропакеты (надстройки), расширяющие возможности ядра ТеХ, например LaTeX или AMSTeX.
18 Численные значения , , и надо взять из таблицы в конце файла. Они должны совпадать с данными, которые использовались Вами в лабораторной работе № 2.
19 Все файлы моделей в пакете Simulink имеют расширение .mdl.
20 При вводе этой и следующих команд окно с графиком не появляется на экране. Чтобы увидеть изменения, надо вручную сделать его активным, щелкнув мышью на соответствующей кнопке в панели задач.
21 Численные значения , , и надо взять из таблицы в конце файла. Они должны совпадать с данными, которые использовались Вами в лабораторных работах № 2 и 3.
22 Значение было определено в лабораторной работе № 2.
23 Скриптом называется файл, содержащий команды Matlab. При его запуске команды выполняются последовательно одна за другой.
24 Численные значения , , и надо взять из таблицы в конце файла. Они должны совпадать с данными, которые использовались Вами в лабораторных работах № 2–4.
25 Значение было определено в лабораторной работе № 2.
26 Номера строк вводить не надо, они отображаются автоматически на полях в окне редактора.
27 Свойство системы сохранять устойчивость и существенные показатели качества при малом изменении характеристик объекта управления в сравнении с расчетными значениями называют грубостью или робастностью (robustness). Негрубые системы непригодны доля использования на практике.
28 Численные значения , , и надо взять из таблицы в конце файла. Они должны совпадать с данными, которые использовались Вами в лабораторных работах № 2–5.
29 Значение было определено в лабораторной работе № 2.
30 Численные значения , , и надо взять из таблицы в конце файла. Они должны совпадать с данными, которые использовались Вами в лабораторных работах № 2–5.
31 Значение было определено в лабораторной работе № 2.
32 Численные значения , , и надо взять из таблицы в конце файла. Они должны совпадать с данными, которые использовались Вами в лабораторных работах № 2–5.
33 Значение было определено в лабораторной работе № 2.
34 Значение было определено в лабораторной работе № 6.






 ,
а «\delta» – букву
.
,
а «\delta» – букву
.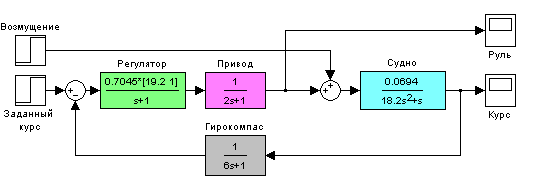
 ,
,
 сек.
Сохраните модель и скопируйте ее в
отчет.
сек.
Сохраните модель и скопируйте ее в
отчет.





 справа от поля Current
Directory
справа от поля Current
Directory

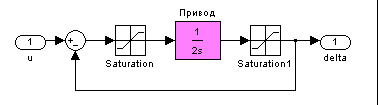



 ),
а через ddMax –
максимальную скорость перекладки
(
),
а через ddMax –
максимальную скорость перекладки
( ).
).