
Анализ инвестиционных программ по вероятным доходам
Анализировать альтернативные инвестиционные программы можно только на основе вероятностного подхода.
Пример: Фирма рассматривает план капиталовложений на ближайшие годы. Берутся четыре варианта: А, Б, В и Г. В табл. 2 приведены расходы на выполнение инвестиционных программ (причем средства должны быть инвестированы в начале первого года), планируемые поступления R в млн. руб. и вероятности поступления наличности. Длительность инвестиционных программ: А – 1 год; Б – 2 года; В – 3 года; Г – 4 года. Планируемые поступления денег происходят в конце года. Ставка дисконтирования считается постоянной и равной i% = 24% годовых. Требуется определить ожидаемый средний доход по четырем вариантам инвестиционных программ и уровень риска.
Таблица 2
Вариант А
n, лет |
S, млн. руб. |
Планир. поступления, Rm |
Вероятность, Pm |
1 |
72 |
100 120 140 160 |
0,2 0,3 0,4 0,1 |
Вариант Б
n, лет |
S, млн. руб. |
Планир. поступления, Rm |
Вероятность, Pm |
1 |
172 |
100 120 140 160 |
0,2 0,3 0,4 0,1 |
2 |
180 210 240 |
0,1 0,3 0,4 |
Вариант В
n, лет |
S, млн. руб. |
Планир. поступления, Rm |
Вероятность, Pm |
1 |
262 |
100 120 140 160 |
0,2 0,3 0,4 0,1 |
2 |
180 210 240 270 |
0,1 0,3 0,4 0,2 |
|
3 |
260 300 340 380 |
0,1 0,4 0,4 0,1 |
Вариант Г
n, лет |
S, млн. руб. |
Планир. поступления, Rm |
Вероятность, Pm |
1 |
420
|
100 120 140 160 |
0,2 0,3 0,4 0,1 |
2 |
180 210 240 270 |
0,1 0,3 0,4 0,2 |
|
3 |
260 300 340 380 |
0,1 0,4 0,4 0,1 |
|
4 |
400 450 500 550 |
0,2 0,3 0,3 0,2 |
Ожидаемое
среднее поступление наличности
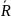 –
это
средневзвешенная величина поступлений
Rm
в
данном варианте. За веса принимаются
вероятности поступления денег Рт:
–
это
средневзвешенная величина поступлений
Rm
в
данном варианте. За веса принимаются
вероятности поступления денег Рт:
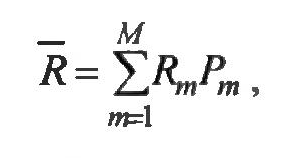
где М – количество планируемых поступлений.
Длительность инвестиционных программ различная, поэтому для анализа альтернативных программ необходимо дисконтировать ожидаемые средние поступления к моменту начала проектов.
Ожидаемый средний доход:
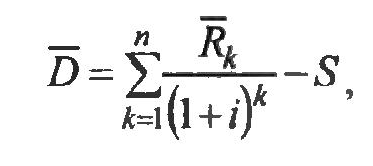
где
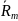 –
средние денежные поступления по годам
для инвестиционной программы, i
– ставка дисконтирования, n
– количество лет, на которые рассчитана
инвестиционная программа. Расчет
ожидаемого среднего дохода дан в табл.
3
–
средние денежные поступления по годам
для инвестиционной программы, i
– ставка дисконтирования, n
– количество лет, на которые рассчитана
инвестиционная программа. Расчет
ожидаемого среднего дохода дан в табл.
3
Таблица 3
m |
n = 1 |
n = 2 |
|||||
Rm, млн. |
Рт |
РтRm, млн. |
Rm, млн. |
Рт |
РтRm, млн. |
||
1 |
100 |
0,2 |
20 |
180 |
0,1 |
18 |
|
2 |
120 |
0,3 |
36 |
210 |
0,3 |
63 |
|
3 |
140 |
0,4 |
56 |
240 |
0,4 |
96 |
|
 =
128
=
128
 =
128
=
128
m |
n = 3 |
n = 4 |
|||||
Rm, млн. |
Рт |
РтRm, млн. |
Rm, млн. |
Рт |
РтRm, млн. |
||
1 |
270 |
0,1 |
26 |
400 |
0,2 |
80 |
|
2 |
300 |
0,4 |
120 |
450 |
0,3 |
135 |
|
3 |
340 |
0,4 |
136 |
500 |
0,3 |
150 |
|
4 |
380 |
0,1 |
38 |
550 |
0,2 |
110 |
|
 =
320
=
320
 =475
=475
Для инвестиционной программы А:
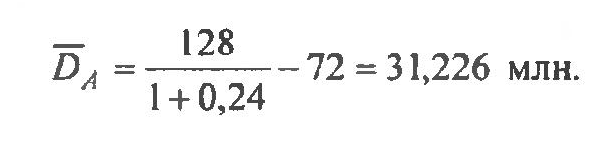
Для инвестиционной программы Б:
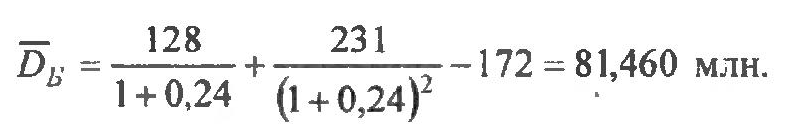
Для инвестиционной программы В:
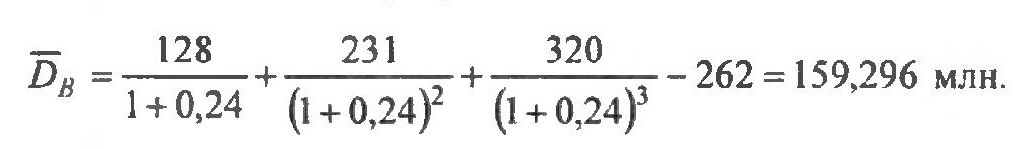
Для инвестиционной программы Г:
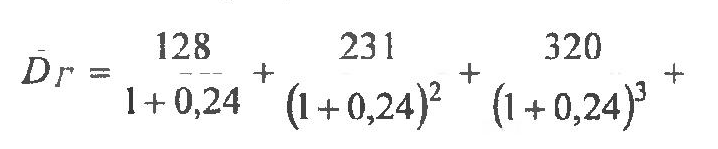
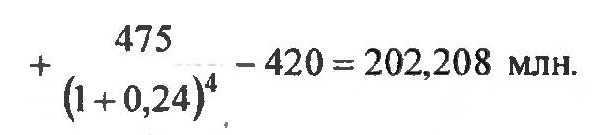
Для оценки риска применяют дисперсию как меру отклонения случайной величины от ожидаемого среднего поступления наличности:
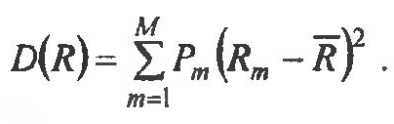
В качестве показателя риска применяют среднее квадратичное отклонение:
![]()
Под относительным риском понимают отношение среднего квадратичного отклонения к ожидаемому среднему доходу инвестиционной программы:
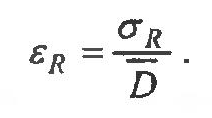
Если поступления наличности независимы друг от друга, то дисперсию инвестиционной программы можно рассчитать следующим образом:
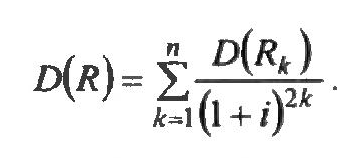
Для сопоставления инвестиционных программ применяют относительный показатель риска ɛR. Расчет дисперсии рассматриваемого примера приведен в табл. 4.
Таблица 4
m |
n = 1 |
n = 2 |
||||
R1-Rm |
Рт |
Рт(R1 -Rm) |
R2-Rm |
Рт |
Рт(R2 -Rm) |
|
1 |
+28 |
0,2 |
156,8 |
+41 |
0,1 |
168,1 |
2 |
+8 |
0,3 |
19,2 |
+11 |
0,3 |
363 |
3 |
-12 |
0,4 |
57,6 |
-9 |
0,4 |
32,4 |
4 |
-32 |
0,1 |
102,4 |
-39 |
0,2 |
304,2 |
|
|
|
||||
m |
n = 3 |
n = 4 |
||||
R3-Rm |
Рт |
Рт(R3 -Rm) |
R4-Rm |
Рт |
Рт(R4 -Rm) |
|
1 |
+60 |
0,1 |
360 |
+75 |
0,2 |
1125 |
2 |
+20 |
0,4 |
160 |
+25 |
0,3 |
187,5 |
3 |
-20 |
0,4 |
160 |
-25 |
0,3 |
1125 |
4 |
-60 |
0,1 |
360 |
-75 |
0,2 |
187,5 |
|
|
|
||||
Для инвестиционной программы A:
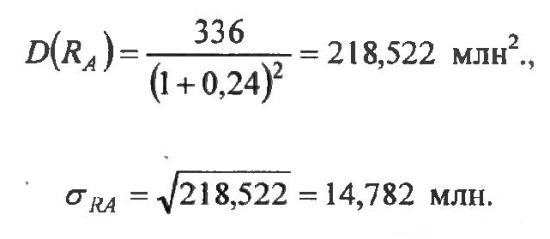
Для инвестиционной программы Б:
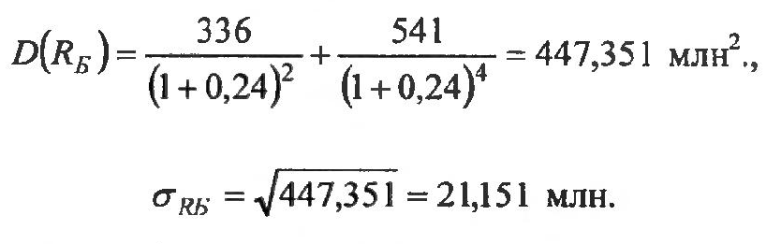
Для инвестиционной программы В:
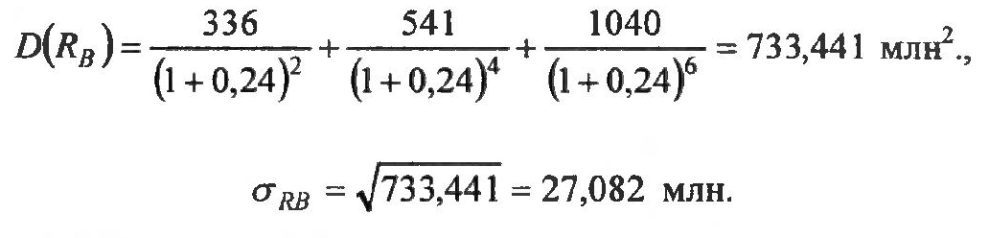
Для инвестиционной программы Г:
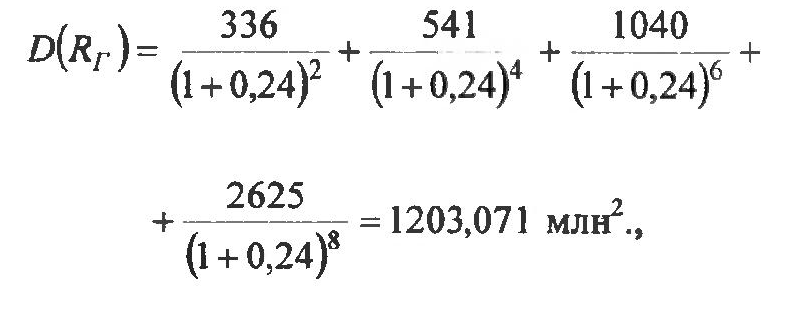
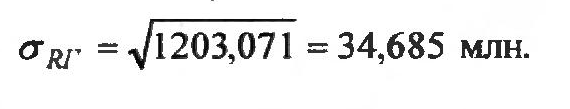
В табл. 5 приведены величины ожидаемого среднего дохода, среднее квадратичное отклонение и относительный коэффициент риска, в последнем столбце – величина ожидаемого среднего дохода в расчете на один год.
Таблица 5
Программа |
|
σ, млн. руб. |
ɛR |
/n, млн. руб. |
А |
31.226 |
14.782 |
0.4734 |
31.226 |
Б |
81.460 |
21.151 |
0.2591 |
40.730 |
В |
159.296 |
27.082 |
0.1700 |
53.099 |
Г |
202.208 |
34.685 |
0.1715 |
20.552 |
Из сопоставления данных следует, что для рассмотренных инвестиционных программ с увеличением длительности их увеличивается доход и снижается коэффициент относительного риска.
Следует отметить, что этот метод анализа инвестиционных программ по их вероятным доходам требует знания о поступлении денег в последующие периоды, что обычно проблематично. Кроме того, принимается, что ставка дисконтирования остается постоянной для всех инвестиционных программ на весь срок их осуществления, что также ограничивает возможности применяемого метода.
Практика показывает, что «средний» бизнесмен стремится избежать повышенного риска и идет на него только в случае высокого дохода. Из всех возможных вариантов инвестиционных программ при одинаковой прибыли выбирается проект с наименьшим риском.
А дальше все зависит от того, какие задачи ставит перед собой владелец капитала. Если его основная задача - наименьший риск, то он будет покупать ценные бумаги с небольшим риском и стабильным средним доходом. Если основная задача бизнесмена - быстрое наращивание капитала, то он будет покупать высоко рискованные акции молодых наукоемких компаний, курсовая стоимость которых может быстро расти. Практика показывает, что лица с небольшим доходом боятся высокого риска и очень осторожны в финансовых делах. Так, по японским данным, в средней семье с годовым доходом 5 млн. йен в акции вкладывается 3,9% капитала, при доходе 10-15 млн. йен –12% капитала, при доходе свыше 100 млн. йен – 16% капитала.
СПИСОК ЛИТЕРАТУРЫ
Аванесов, Э.Т. Инвестиционный анализ. – Мн.: БГУ, 2002.
Башарин, Г.П. Начала финансовой математики. – М.:Инфра – М, 1997.
Брейли Р., Майерс, С. Принципы корпоративных финансов: Пер. с англ. – М.: ЗАО «Олимп-Бизнес», 1997.
Бухвалов, А.В., Идельсон, А.В. Самоучитель по финансовым расчетам. – М.: Мир, Пресс-Сервис, 1997.
Капельян, С.Н., Левкович, О.А. Основы коммерческих и финансовых расчетов. – Мн.: НТЦ «АПИ», 1999.
Капитоненко, В.В. Финансовая математика и ее приложения: учеб.-практ. пособие для вузов. – М.: Издательство ПРИОР, 1998.
Ковалев, В.В., Уланов, В.А. Курс финансовых вычислений. – М.: Финансы и статистика, 2001.
Ковалев, В.В., Уланов, В.А. Введение в финансовую математику: учеб. пособие.- СПб., 1997.
Ковалев, В.В., Уланов, В.А. Простые проценты в коммерческих вычислениях: учеб. пособие. - СПб., 1997.
Мелкумов, Я.С. Теоретическое и практическое пособие по финансовым вычислениям. – М.: Инфра-М, 1996.
Четыркин, Е.М. Финансовая математика: учеб. – М.: Дело, 2001.

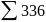
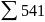
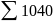
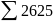
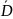 ,
млн.
руб.
,
млн.
руб.