Тема 1: Начисление процентов

1. Начисление процентов и налоги

Налогообложение играет большую роль в экономике любой страны. Во многих странах налогом облагают проценты, полученные при помещении некоторой суммы на депозит, что уменьшает реальную наращенную сумму и реальную доходность финансовой операции. 

Налоги, начисляемые на полученные проценты, уменьшают реальную доходность финансовой операции. Учет налога при определении наращенной суммы приводит к уменьшению ставки.

Введем обозначения:

t- ставка налога на проценты

T – общая сумма налога

F- наращенная сумма до выплаты налога на проценты

F_t - наращенная сумма после выплаты налога на проценты

P – вложенная сумма 

n – продолжительность финансовой операции

Пусть r - простые ссудные проценты, тогда величина процентов, начисленных за период n, равна Pnr.

Сумма налога на начисленные проценты равна ^ Т=Pnrt  (1)

Наращенная сумма после выплаты налога на проценты равна 

F_t = P[(1+r(1-t)n] (2)

Таким образом, налог на проценты уменьшает процентную ставку и вместо ставки r применяется ставка (1-t)r.

Пусть на сумму ^ Р за период времени n начислялись простые учетные проценты по учетной ставке d. Величина начисленных процентов равна Pnd/(1-nd).

Сумма налога на начисленные проценты составит 

T=Pndt/(1-nd) (3)

Наращенная сумма после выплаты налога на проценты равна 

F_t = F-T=P(1-ndt)/(1-nd) (4)

Пусть r - сложные ссудные проценты, тогда величина процентов, начисленных за период n, равна P[(1+r)ⁿ-1]

Сумма налога на начисленные проценты равна 

Т=P[(1+r)ⁿ -1]t  (5)

Наращенная сумма после выплаты налога на проценты равна 

F_t =P[(1+r)ⁿ (1-t)+t] (6)

В случае сложных процентов налог на начисленные проценты можно выплачивать как в конце финансовой операции, так и каждый год. При этом общая сумма исчисленного налога не изменяется.

Пусть на сумму ^ Р за период времени n начислялись сложные учетные проценты по учетной ставке d. Величина начисленных процентов равна:

Сумма налога на начисленные проценты равна  (7)

Наращенная сумма после выплаты налога на проценты равна:  (8)

Пусть на сумму Р за период времени n начислялись непрерывные проценты по ставке δ.

Сумма налога на начисленные проценты равна 

T=P(e^δ -1)t (9)

F_t =P[e^δ (1-t)+t] (10)

Задача 1. На депозит поместили 300 тыс. руб. на полтора года. Банк начисляет простые учетные проценты по ставке под 14% годовых. Определить наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты составляет 12% годовых. Решение Используем формулу (8.4) при P=300; n=1,5; t=0,12; d=0,14

F_t =300(1-1,5∙0,14∙0,12)/ (1-1,5∙0,14)= 370,018

Наращенная сумма с учетом налога на проценты составит 370018 руб. Задача 2. На депозит поместили 300 тыс. руб. на полтора года. Банк начисляет простые проценты по ставке под 16% годовых. Определить наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты составляет 12% годовых.

Решение Используем формулу (8.2) при P=300; n=1,5; t=0,12; r=0,16

F_t =300[1+∙0,16 (1-∙0,12)1,5]= 360,336

Наращенная сумма с учетом налога на проценты составит 360336 руб. Задача 3. На вклад в 2 млн. руб. в течение 4 лет каждые полгода начислялись сложные проценты по годовой номинальной ставке 12% годовых. Определить наращенную сумму после уплаты налога на проценты, если ставка налога на проценты составляет 8% годовых.

Решение Запишем формулу (8.6) с учетом полугодового начисления процентов:

F_t =P[(1+r/m)^nm (1-t)+t] 

при P=2; r=0,12; n=4; m=2; t=0,08

F_t = 3,09268

Наращенная сумма с учетом налога на проценты составит 3 092 680 руб.

2. Проценты и инфляция

1. Основные понятия

Инфляция – это обесценивание денег, обусловленное чрезмерным увеличением выпущенной в обращение массы бумажных денег и безналичных выплат по сравнению с реальным предложение платных товаров и услуг.

Обратный процесс – дефляция – изъятие из обращения части избыточной денежной массы, комплекс мер по сдерживанию или уменьшению инфляция. Дефляция – это процесс уменьшения цен. Процесс дефляции характерен для случая, когда экономика находится в состоянии глубокого кризиса, проявляется инфляция в росте цен на товары. На одни товары цены могут расти, на другие – уменьшаться, но если наблюдается устойчивая тенденция массового повышения цен, то это уже инфляция.

Изменение цен на товары и услуги определяется при помощи индекса цен. Индекс цен численно равен отношению цен на товары, услуги или работы в один период времени к ценам этих же товаров, услуг или работ в другой период времени.

И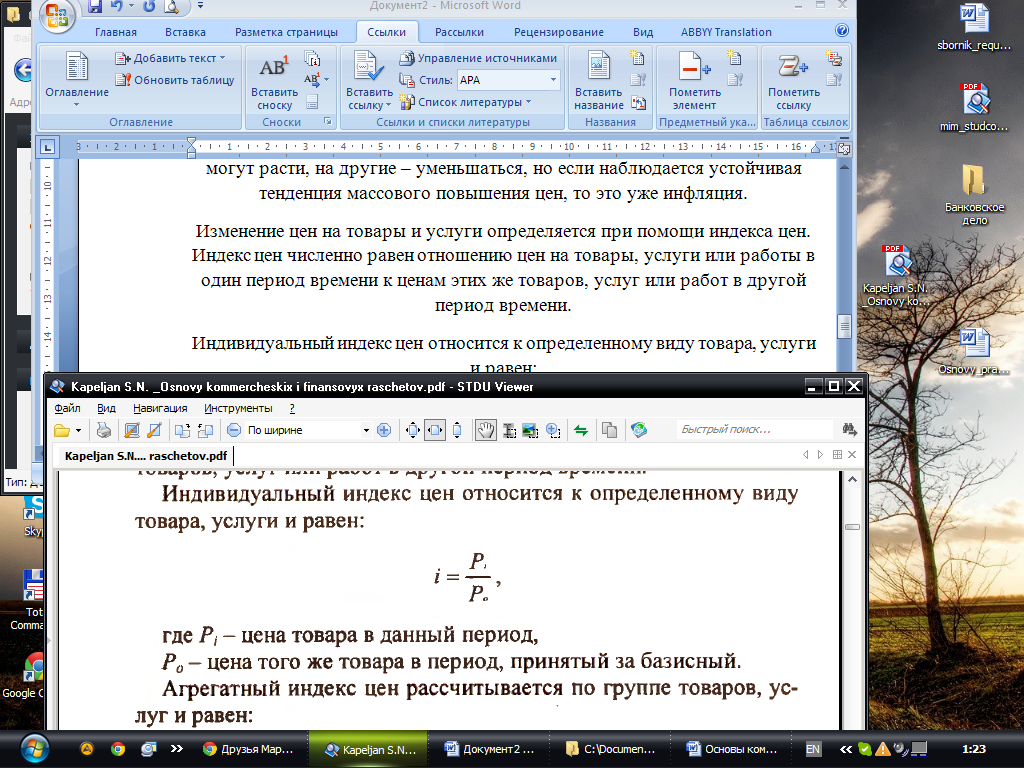 ндивидуальный индекс цен относится к определенному виду товара, услуги и равен:

где Pi- цена товара в данный период,

Po – цена того же товара в период, принятый за бпзисный.

Агрегатный индекс цен рассчитывается по группе товаров, услуг и равен:

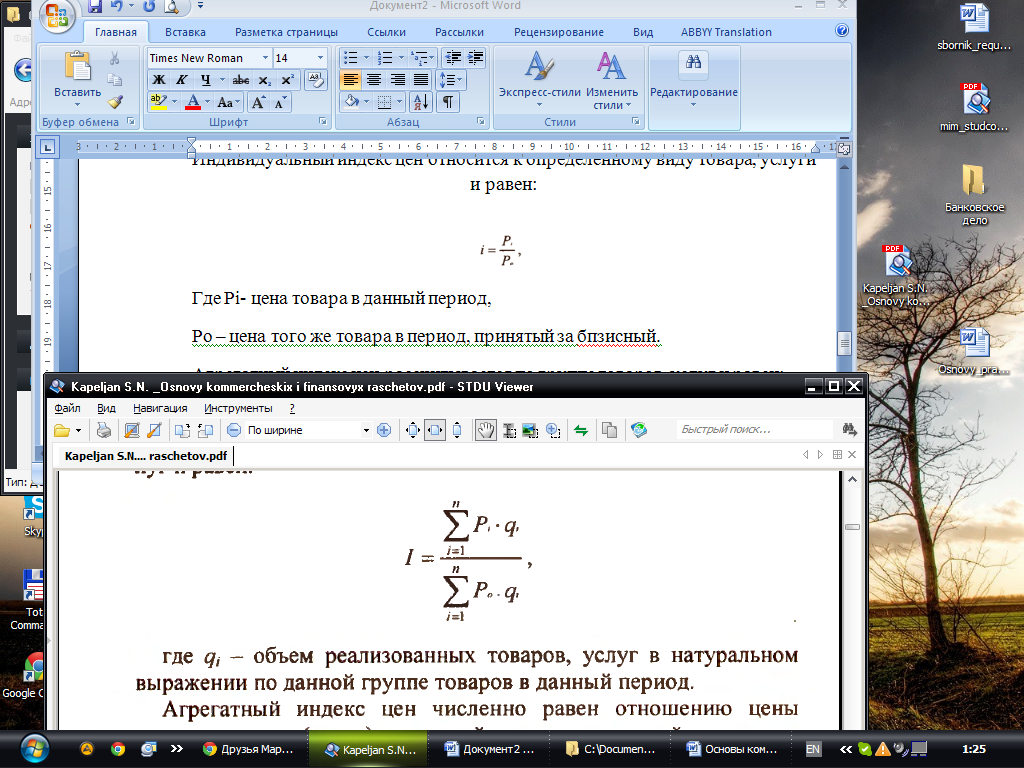
где qi – объем реализованных товаров, услуг в натуральном выражении по данной группе товаров в данный период.

Агрегатный индекс цен численно равен отношению цены группы товаров (услуг) за данный период к цене той же группы товаров (услуг) в базисном периоде.

Индекс цен на потребительские и промышленные товары регулярно публикуется.

Коэффициент падения покупательной способности денег определяется как величина, обратная индексу цен.

Индекс потребительских цен определяется по стоимости «потребительской корзины».

Процентное изменение индекса потребительских цен называется уровнем инфляции.

Пусть S – некоторая сумма денег, имеющаяся у клиента в данный момент; St- сумма денег через время t, покупательная способность которой равна S. Вследствие инфляции St >S и St =S+S, где S – некоторая сумма денег, которая добавляется к S для сохранения покупательной способности. Под средним уровнем инфляции за какой-то период времени понимается

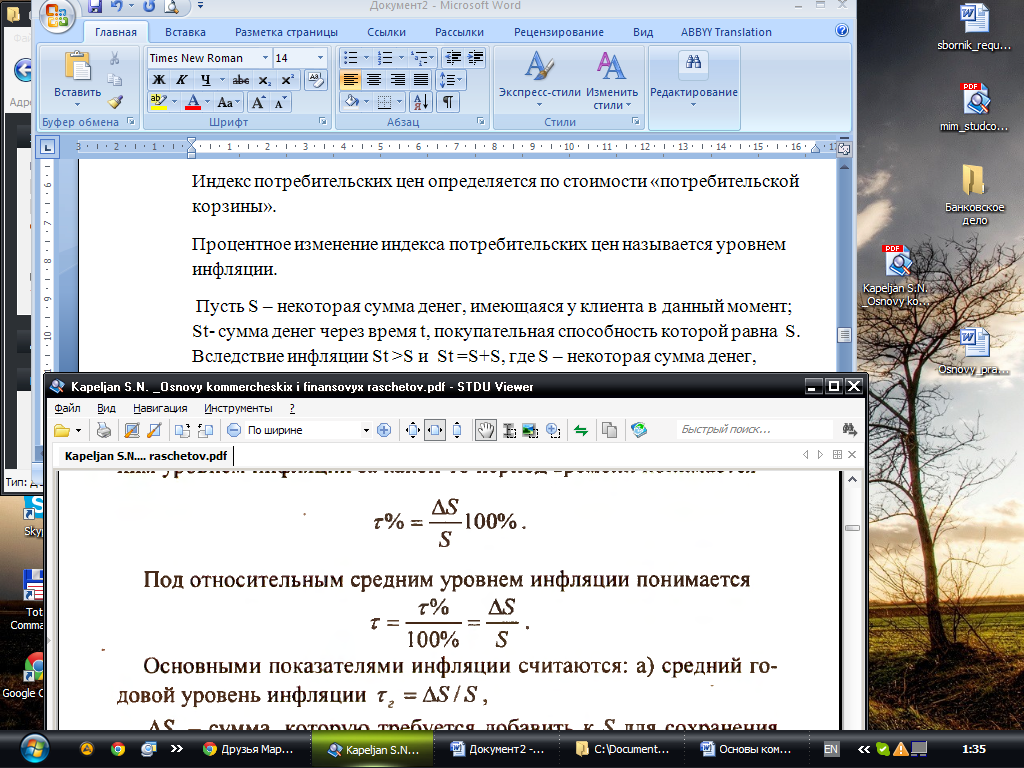
Под относительным средним уровнем инфляции понимается:

О сновными показателями инфляции считаются: а) средний годовой уровень инфляции

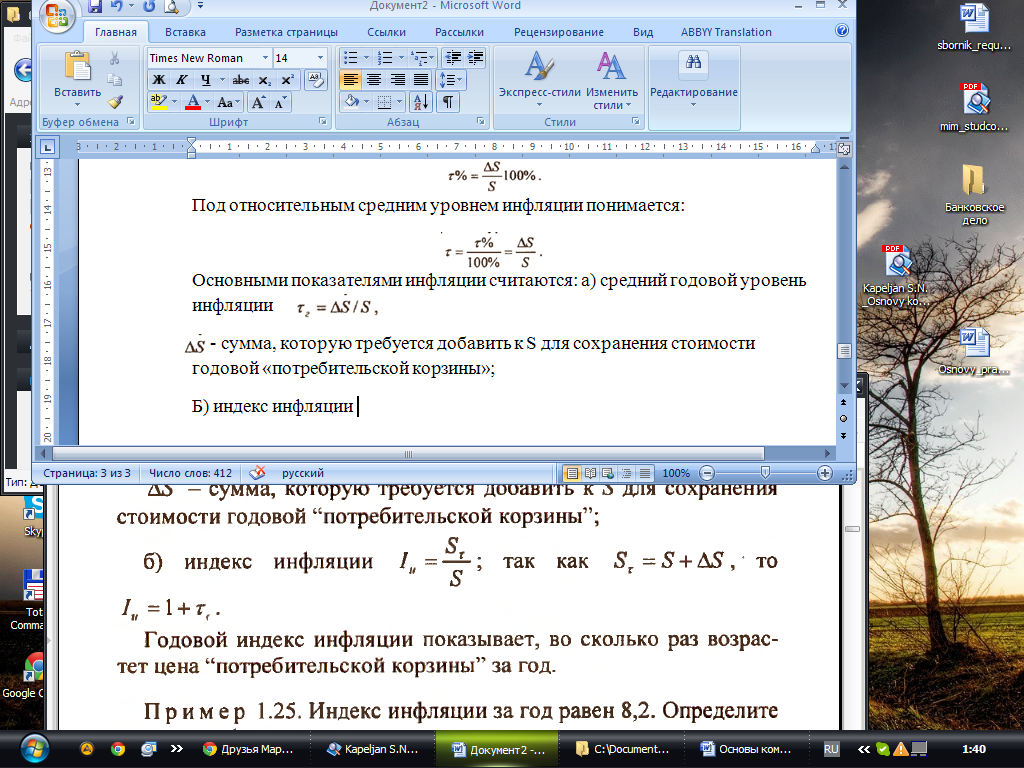- сумма, которую требуется добавить к S для сохранения стоимости годовой «потребительской корзины»;

Б ) индекс инфляции ; так как то

Годовой индекс инфляции показывает, во сколько раз возрастает цена «потребительской корзины» за год.

Различают три вида инфляции: а) умеренная, или ползучая, инфляция с годовым уровнем инфляции от 3 до 10% в год. Стоимость денег соответственно сокращается; б) галопирующая, или открытая, инфляция при уровне инфляция при уровне инфляции от 10 до 20% в год. Потребители ускоренно стараются материализовать деньги в товары. В выигрыше оказываются заемщики, так как уменьшается стоимость кредитов; в) гиперинфляция при годовом уровне инфляции свыше 100%. При инфляции население пытается вложить деньги в активы, не подверженные инфляции, или в стабильную валюту.

2. Простые проценты и инфляция

Пусть годовая процентная ставка равна i. Наращенная сумма за год: S=P(1+i). С учетом инфляции, годовой уровень которой равен t_г, инвесторов устраивает такая годовая процентная ставка, которая бы обеспечивала прибыль от наращения по годовой ставке i и покрывала потери от инфляции. Обозначим эту годовую процентную ставку i_t . Тогда с учетом инфляции S_t=p(1+i_t).

С другой стороны, S_t=S(1+t_г)=p(1+i)(1+t_г). Приравнивая, получим:

Н аращенная сумма с учетом инфляции:

K _{Hu –} коэффициент наращения с поправкой на инфляцию.

Е сли срок кредита, или депозита, составляет дней при годовой процентной ставке i и годовом уровне инфляции t, то величина наращенной суммы

О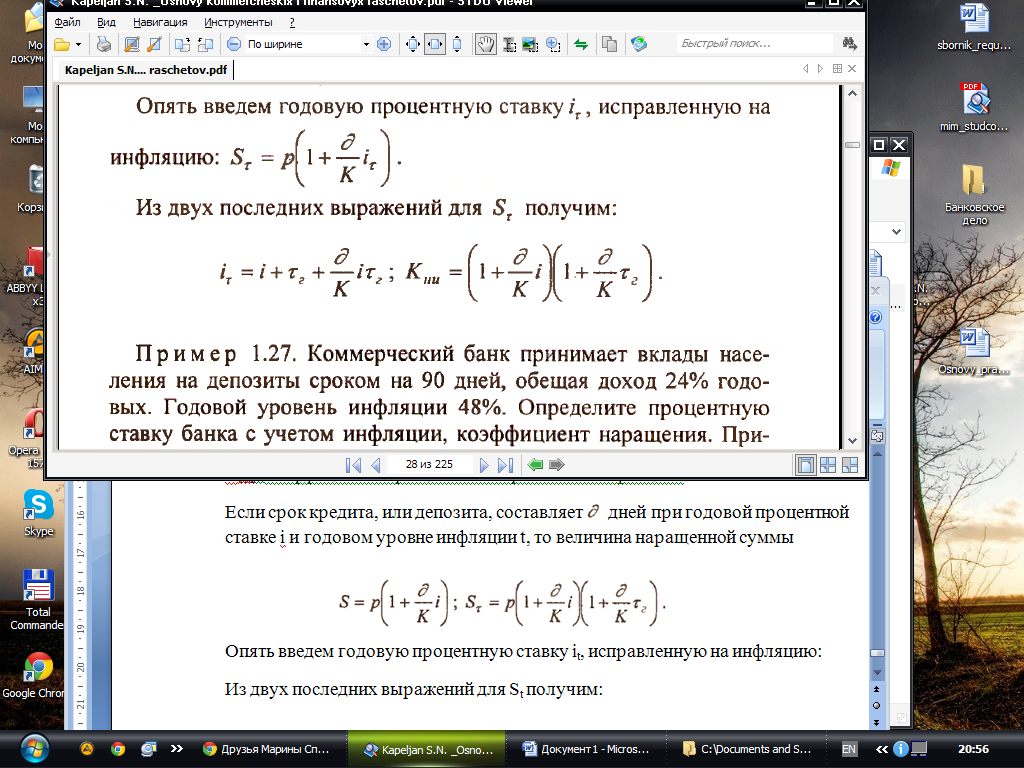 пять введем годовую процентную ставку i_t, исправленную на инфляцию:

И з двух последних выражений для S_t получим:

О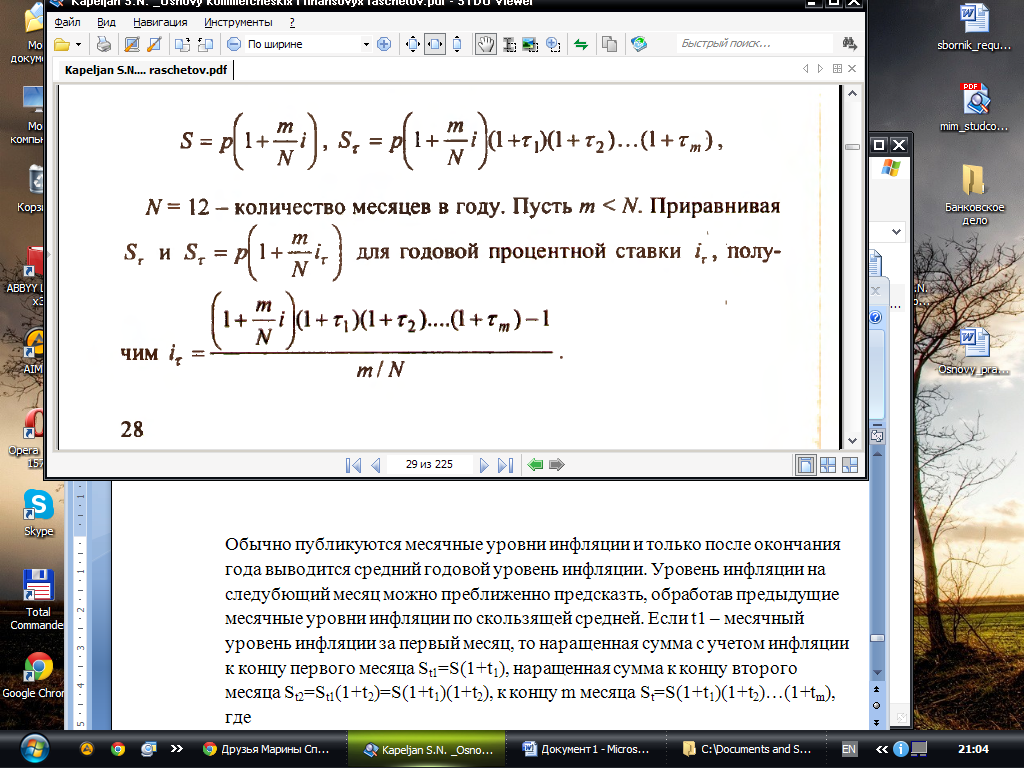 бычно публикуются месячные уровни инфляции и только после окончания года выводится средний годовой уровень инфляции. Уровень инфляции на следубющий месяц можно преближенно предсказть, обработав предыдущие месячные уровни инфляции по скользящей средней. Если t1 – месячный уровень инфляции за первый месяц, то наращенная сумма с учетом инфляции к концу первого месяца S_t1=S(1+t₁), наращенная сумма к концу второго месяца S_t2=S_t1(1+t₂)=S(1+t₁)(1+t₂), к концу m месяца S_t=S(1+t₁)(1+t₂)…(1+t_m), где

N =12 – количество месяцев в году. Пусть m<N.

Приравнивая и для годовой процентной ставки, получим

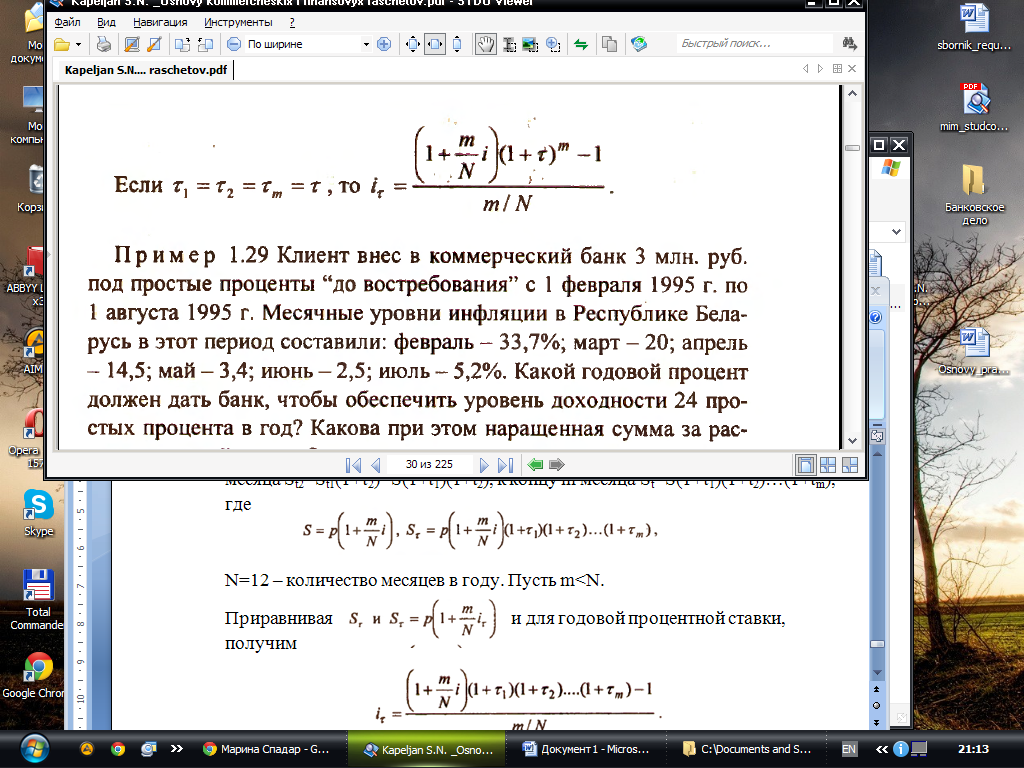
3. Сложные проценты и инфляция

Наращенная сумма по формуле сложных процентов S=p(1+i_c)ⁿ.

С учетом инфляции наращенная сумма, обеспечивающая такую же доходность,

г де - годовые уровни инфляции за первый год, второй и т.д.

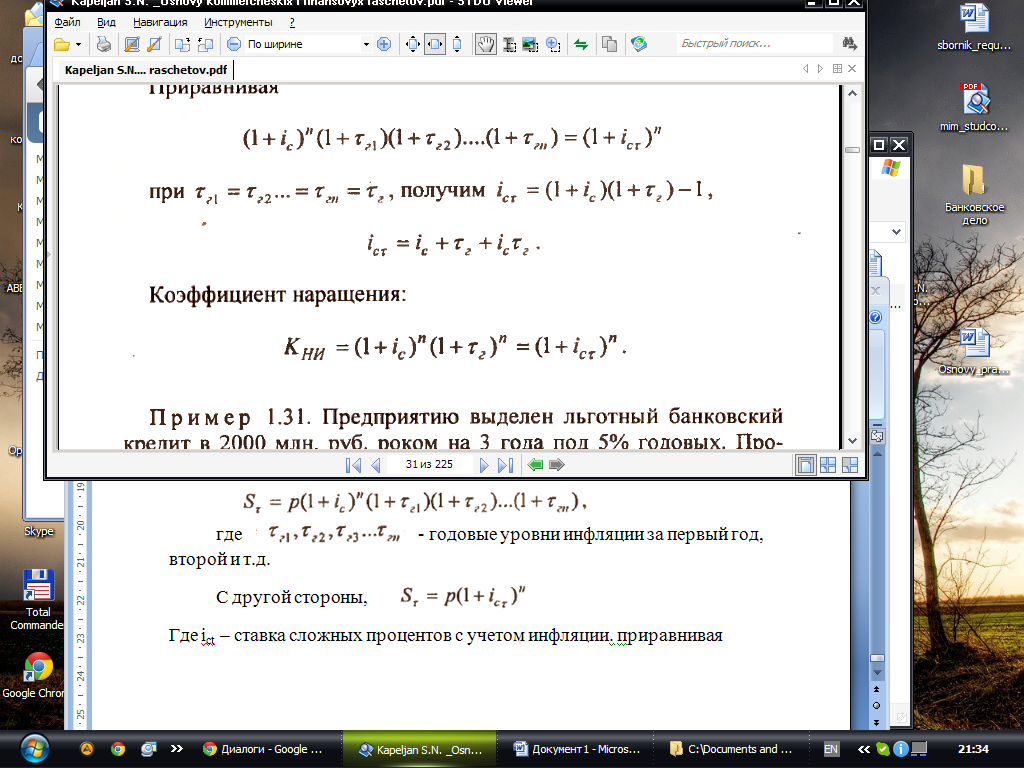
С другой стороны,

Где i_ct – ставка сложных процентов с учетом инфляции. Приравнивая

Е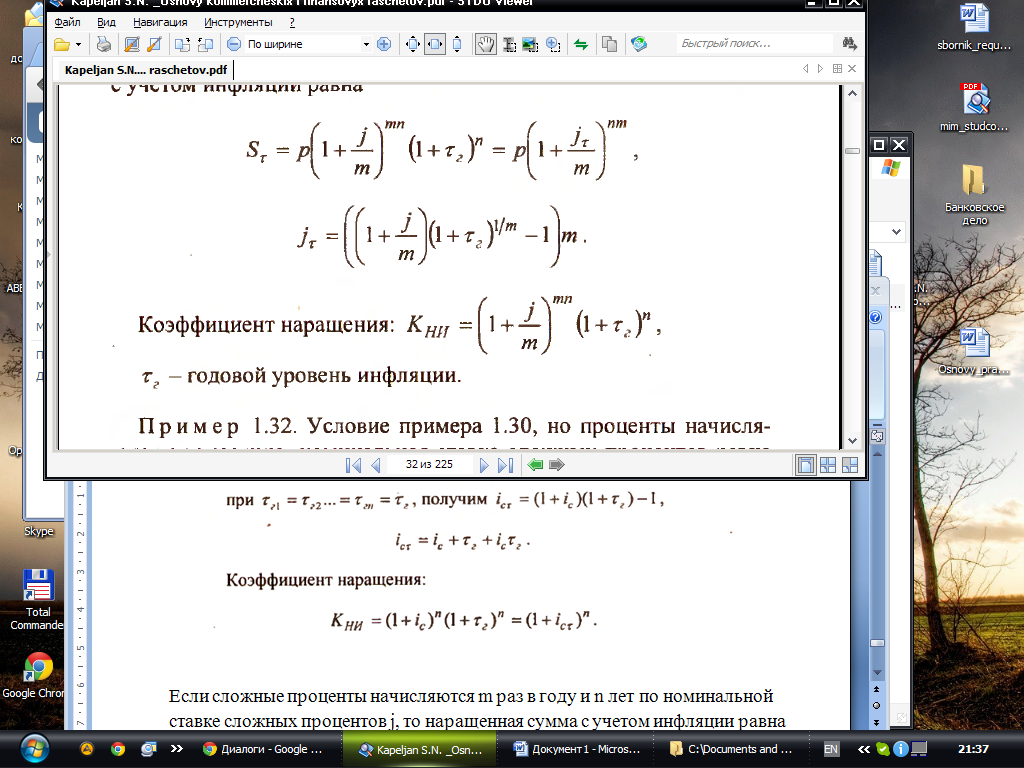 сли сложные проценты начисляются m раз в году и n лет по номинальной ставке сложных процентов j, то наращенная сумма с учетом инфляции равна

Коэффициент наращения:

t_г – годовой уровень инфляции.