Сравнение преимуществ и ограничений мер центральной тенденции
Мера |
Преимущества |
Ограничения |
Среднее. «Центр тяжести» данных. Равно сумме значений всего ряда данных, деленной на количество этих значений |
Выборочная стабильность – менее всего изменяется от выборки к выборке. Поддается математической обработке: может быть использована при подсчете дальнейших статистик. Отражает действительную ценность каждого показателя и поэтому содержит больше информации, относящейся к полному набору данных |
Не используется: – если распределение скошено; – когда значение экстремальных случаев неизвестно. Не используется в номинальной и порядковой шкалах |
Медиана. Разделяет предварительно упорядоченные данные на две равные по размеру части |
Лучше всего репрезентирует центр сильно скошенного распределения (не подвержена влиянию экстремальных значений). Может быть подсчитана, когда экстремальные значения неизвестны |
Зависит от величины принятого интервала (для сгруппированных данных). Редко используется в дальнейших статистиках. Не используется в номинальной шкале |
Мода. Самый типичный случай |
Полезна для неупорядоченных качественных переменных. Быстро дает представление о типичном по группе. Ее очень легко посчитать. Мало чувствительна к экстремальным значениям |
Зависит от принятого интервала (для сгруппированных данных). Редко используется в дальнейших статистиках. Может отсутствовать для некоторых сгруппированных данных |
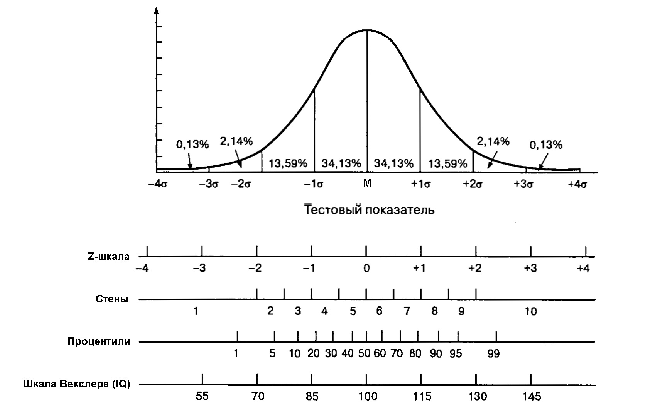
Рис. 1. Соотношение нормального распределения и показателей различных стандартизированных шкал
Виды эмпирических графикОв распределения
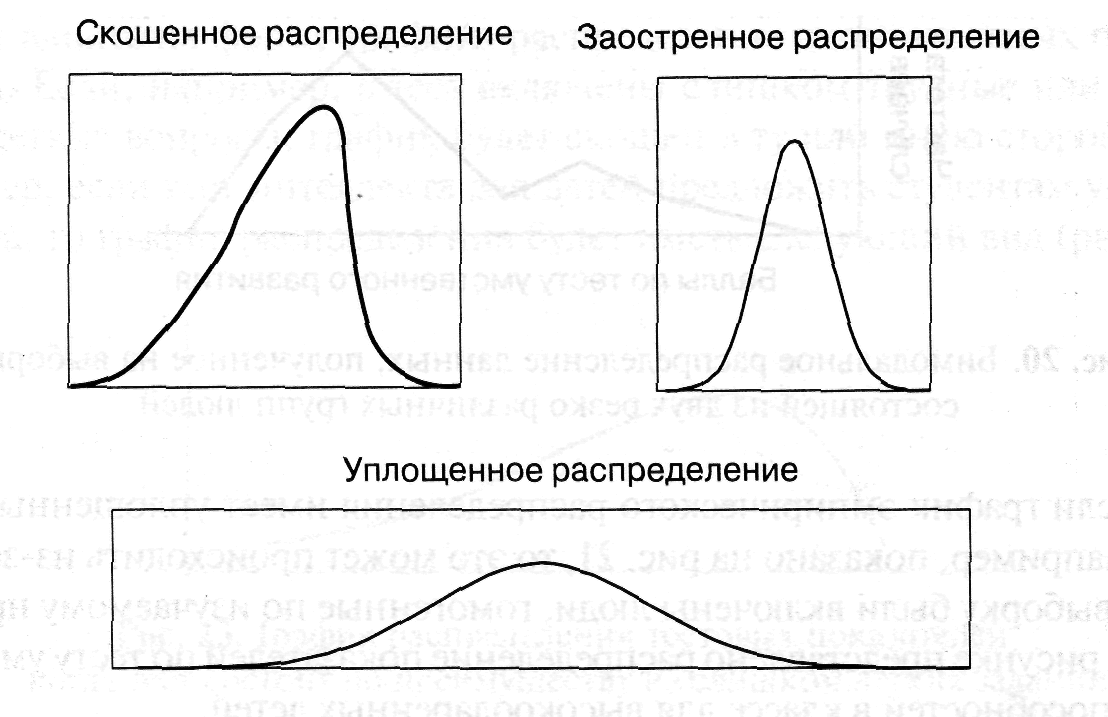
Рис.1. Вид возможных эмпирических распределений
Рис.2. Скошенное распределение данных, полученных на выборке,
состоящей из 2-х различных групп
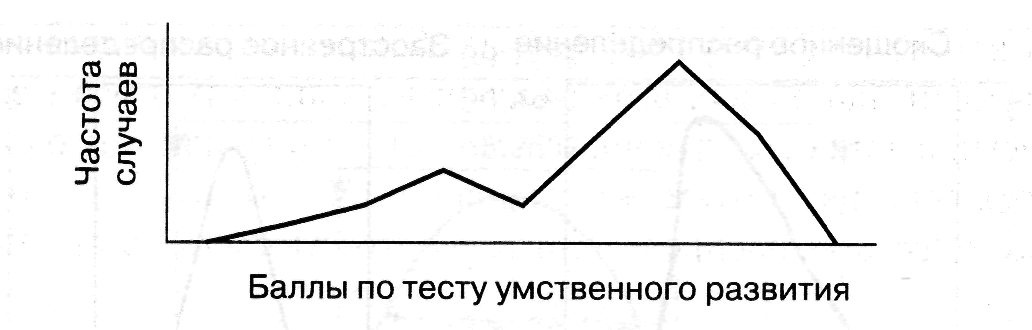
Рис. 3. Бимодальное распределение данных, полученное на выборке,
состоящей из 2-х резко различных групп людей
Рис.4. Распределение данных, полученных на гомогенной выборке
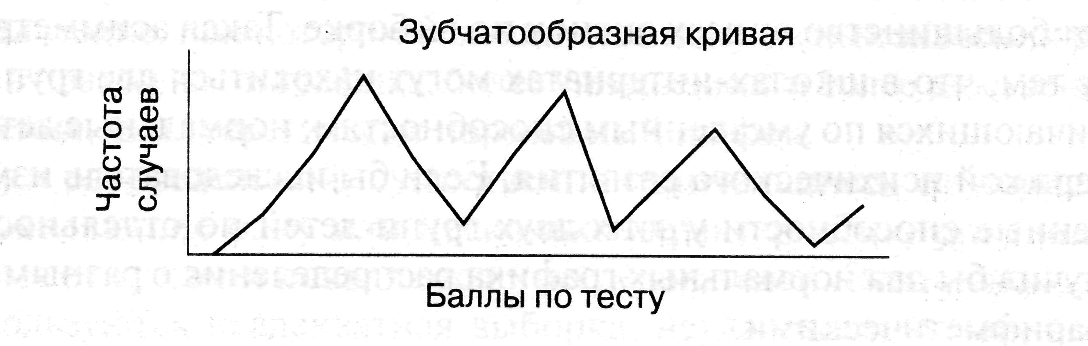
Рис.5. Распределение данных, полученных на слишком маленькой выборке
Рис.6. График распределения тестовых показателей,
когда тест состоит по преимуществу из лёгких заданий
Этапы проверки статистических гипотез
Формулировка основной гипотезы H0 и конкурирующей гипотезы H1. (Гипотезы должны быть чётко формализованы в математических терминах.)
Задание вероятности p (α), называемой уровнем значимости, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы.
Расчёт статистики, такой, что:
её величина зависит от исходной выборки;
по её значению можно делать выводы об истинности гипотезы H0;
сама статистика должна подчиняться какому-то известному закону распределения.
Построение критической области, по которой можно судить о существенных расхождениях с предположением.
Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику и по попаданию (или непопаданию) в критическую область выносится решение об отвержении (или принятии) выдвинутой гипотезы H0.
Классификация методов сравнения
КЛАССИФИКАЦИЯ ЗАДАЧ И МЕТОДОВ ИХ РЕШЕНИЯ
Тема: «Вычисление параметров распределения в EXCEL и SPSS»
Задание № 3.1