2. Расчетно-конструктивная часть

2.1. Расчет предварительно напряженной пустотной плиты перекрытия

Плита перекрытия - предварительно напряженная пустотная с номинальной шириной, равной 1 500 мм; длиной – 3 300 мм.

2.1.1. Расчет пустотной плиты

по предельным состояниям первой группы

2.1.1.1. Расчетный пролет и нагрузки. При опирании на стены расчетный пролет l₀ = l – 0,12 = 3,3 – 0,12 ≈ 3,2 м.

Подсчет нагрузок на 1 м² перекрытия приведен в табл. 2.1.

Таблица 2.1

Нормативные и расчетные нагрузки на 1м² перекрытия

Вид нагрузки	Нормативная нагрузка, Н/м2	Коэффициент надежности по нагрузке	Расчетная нагрузка, Н/м2
Постоянная: пустотная плита перекрытия Слой ЦПР толщ. 20 мм, 2200 кг/м3 Керамические плитки, t=13мм, 1800 кг/м3	3 000 440 240	1,1 1,3 1,1	3 300 570 264
ИТОГО: Временная в том числе: длительная кратковременная	3 680 2 000 1 500 500	1,2 1,2 1,2	4 134 2 400 1 800 600
Полная нагрузка в том числе: постоянная и длительная	5 680 5 180	-	6 534 -

Постоянную нагрузку обозначим g , а временную - , полную - g + .

Расчетная нагрузка на 1 м длины при ширине плиты 1,5 м с учетом коэффициента надежности по назначению здания _n = 0,95 :

постоянная g = 4,134 ^. 1,5 ^. 0,95 = 5,9 кН/м,

полная g +  = 6,534 ^. 1,5 ^. 0,95 = 9,3 кН/м.

Нормативная нагрузка на 1 м:

постоянная g = 3,68 ^. 1,5 ^. 0,95 = 5,2 кН/м,

полная g +  = 5,68 ^. 1,5 ^. 0,95 = 8,1 кН/м,

в том числе постоянная и длительная 5,18 ^. 1,5 ^. 0,95 = 7,4 кН/м.

Усилия от расчетных и нормативных нагрузок.

Усилия от полной расчетной нагрузки:

М = ( g +  ) ^. l₀² / 8 = 9,3 ^. 3,2 ² / 8 = 14,2 кНм;

Q = ( g +  ) ^. l₀ / 2 = 9,3 ^. 3,2 / 2 = 16,3 кН;

от нормативной полной нагрузки:

М = ( g +  ) ^. l₀² / 8 = 8,1 ^. 3,2 ² / 8 = 12,4 кНм;

Q = ( g +  ) ^. l₀ / 2 = 8,1 ^. 3,2 / 2 = 14,2 кН;

от нормативной постоянной и длительной нагрузки:

М = 7,4 ^. 3,2 ² / 8 = 11,3 кНм

2.1.1.2. Размеры сечения плиты

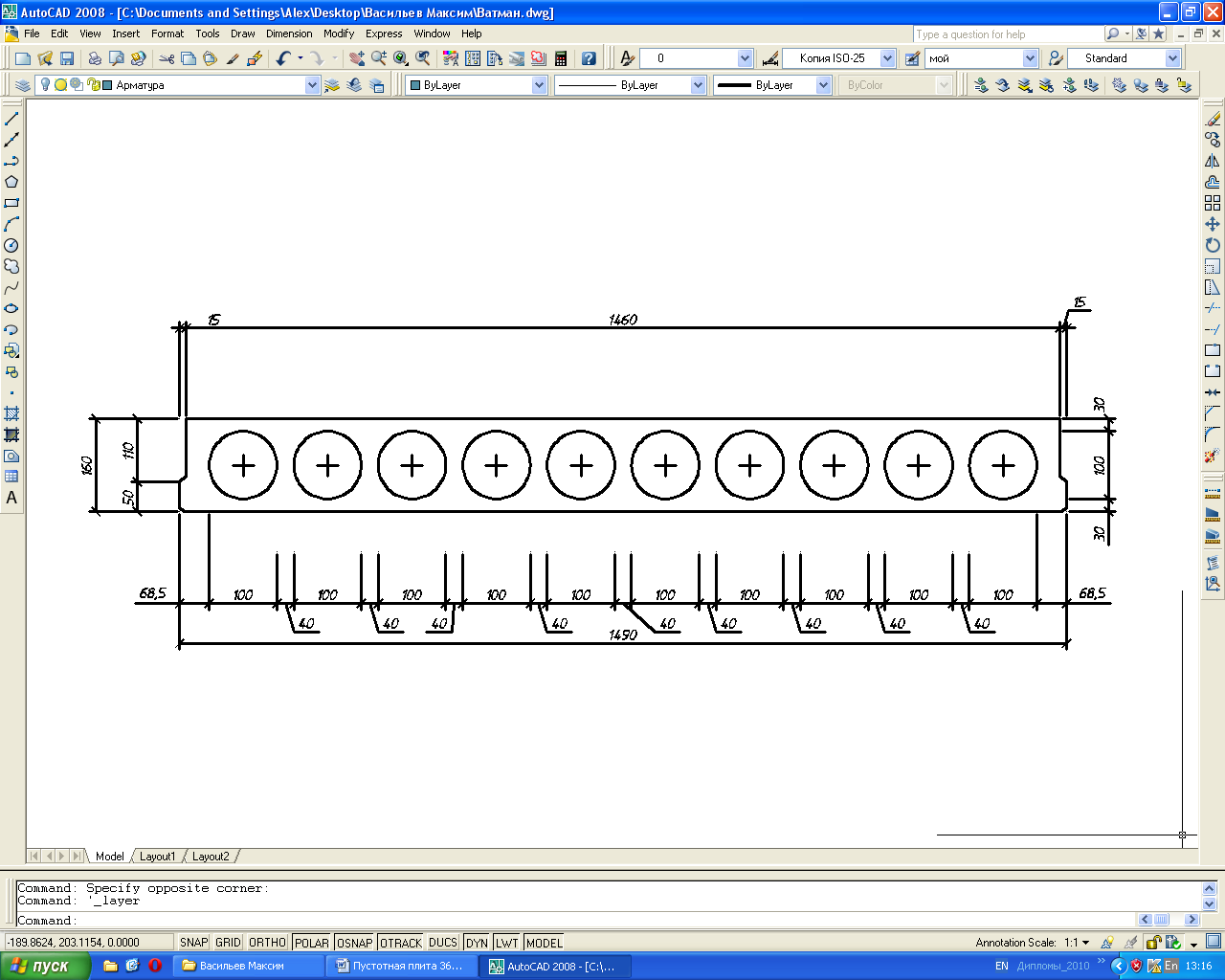
Рис. 2.1. Размеры сечения плиты

Высота сечения пустотной предварительно напряженной плиты (10 круглых пустот диаметром 100 мм)

h = l₀ / 30 = 320 / 30 = 12 см; принимаем h = 16 см.

Рабочая высота сечения h₀ = h - a = 16 - 3 = 13 см.

Размеры: толщина верхней и нижней полок (16 – 10) 0,5 = 3,0 см. Ширина ребер: средних – 4,0 см, крайних – 5,0 см.

В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки таврового сечения h^/_f = 3,0 см.

Отношение h ^/_f / h = 3,0 / 16 = 0,19 > 0,1; при этом в расчет вводим всю ширину полки b ^/_f = 146 см.

Расчетная ширина ребра b = 146 - 10 ^. 10 = 46 см.

2.1.1.3. Характеристики прочности бетона и арматуры

Пустотная предварительно напряженная плита армируется арматурой класса А-V с электротермическим натяжением на упоры.

К трещиностойкости плиты предъявляются требования 3-й категории. Изделие подвергается тепловой обработке при атмосферном давлении.

Бетон тяжелый, класс В40, соответствующий классу напрягаемой арматуры.

Призменная прочность бетона:

нормативная R_bn = R_b,сеч = 29 МПа;

расчетная R_b = 22 МПа;

нормативное сопротивление при растяжении

R_btn = R_bt,сеч = 2,1 МПа ;

расчетное сопротивление при растяжении R_bt = 1,4 МПа;

коэффициент условий работы бетона _b2 = 0,9;

начальный модуль упругости бетона E_b = 32500 МПа.

Передаточная прочность бетона R_bp устанавливается такой, чтобы при обжатии отношение напряжений _bp / R_bp < 0,75 .

Арматура продольных ребер класса А800 (А-V). Нормативное сопротивление арматуры R_sn = 785 МПа; расчетное сопротивление R_s = 680 МПа; модуль упругости E_s = 190 000 МПа.

Предварительное напряжение арматуры

_sp = 0,75 ^. R_sn = 0,75 ^. 785 = 589 МПа.

При электротермическом способе натяжения

p = (30 + 360 / l ) = 30 + 360 / 3,3 = 130 МПа,

где l - длина натягиваемого стержня (длина плиты);

_sp + р = 589 + 130 = 719 < R_sn = 785 МПа - условие выполняется.

Вычисляем предельное отклонение предварительного напряжения:

_sp = 0,5( р / _sp ) ^. ( 1 + ( 1 / ( n_p )^1/2 ) = [( 0,5 ^. 130 ) / 589] ^. [ 1 + 1 / ( 4 ) ^1/2 ]=

= 0,17, где n_p = 4 - число напрягаемых стержней плиты.

Коэффициент точности натяжения при благоприятном влиянии предварительного напряжения

_sp = 1 - _sp = 1 - 0,17 = 0,83;

при проверке на образование трещин в верхней зоне плиты при обжатии

_sp = 1 + _sp = 1 + 0,17 = 1,17

Предварительное напряжение с учетом точности натяжения

_sp = 0,83 ^. 589 = 489 МПа.

2.1.1.4. Расчет прочности плиты по сечению, нормальному к продольной оси

Сечение тавровое с полкой в сжатой зоне. М = 14,2 кНм

Вычисляем коэффициент

_m = M / (_b2 ^. R_b ^. b^\_f ^. h₀² ) = ( 1420 ^. 10³ ) / ( 0,9 ^. 22 ^. 146 ^. 13 ² (100) ) = 0,03 ; по таблице найдем  = 0,03;  = 0,985.

Х =  ^. h₀ = 0,03 ^. 13 = 0,4 < 3,0 см - нейтральная ось проходит в пределах сжатой полки.

Вычисляем характеристику деформативных свойств бетона сжатой зоны

 = 0,85 - 0,008 ^. _b2 ^. R_b = 0,85 - 0,008 ^. 22 ^. 0,9 = 0,69.

Вычисляем граничную высоту сжатой зоны по формуле

_R =  / [ 1 + (_R / 500 ) ^. ( 1 -  / 1,1)] = 0,69 / [ 1 + ( 491 / 500 ) ^.x

x ( 1 - 0,69 / 1,1)] = 0,5,

где _R = R_S + 400 - _sp - _R = 680 + 400 - 589 = 491 МПа;

_R = 0; в знаменателе выражения принято 500 МПа, поскольку _b2 < 1.

Коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести, согласно формуле

_s6 = --1] ^. [(2 /_R)-1]=1,15-[1,15-1 ] ^. [(2 ^. 0,03 / 0,5)-1 ] = 1,24 >  ,

где  = 1,15 для арматуры класса А-V.

Принимаем _s6 =  = 1,15.

Вычисляем площадь сечения растянутой арматуры

А_s = М / (_s6 ^. R_S ^.  ^. h₀ ) = 1420 ^. 10³ / ( 1,15 ^. 680 ^. 0,985 ^. 13 (100)) = 1,4 см²

Принимаем 4  10 класса A-800 (А-V) с А_s = 3,14 см².