5. Система рівнянь методу скінченних різниць

Система рівнянь методу скінченних різниць для згину тонкої плити має вигляд:

,

Розв’язуємо вищенаведену систему лінійних алгебраїчних рівнянь методом оберненої матриці, використовуючи електронну таблицю MS Excel.

Матриця і вектор вільних членів системи рівнянь:

Матриця							Вектор
23	-8	-8	2	1	0		8.74E-02
-16	21	2	-8	0	1		8.74E-02
-8	2	22	-8	-8	2		8.74E-02
2	-8	-16	20	2	-8		8.74E-02
1	0	-8	2	21	-8		8.74E-02
0	1	4	-8	-16	19		8.74E-02

Обернена матриця:

0.091472	0.042683998	0.0668657	0.04002357	0.0339672	0.021869
0.099464	0.106183032	0.1025528	0.08554731	0.0605788	0.0451432
0.067583	0.039697875	0.1451783	0.0793189	0.0835456	0.0512032
0.101122	0.082952749	0.1848176	0.17586199	0.1282551	0.1042289
0.030278	0.019409802	0.0743018	0.04666367	0.1152402	0.0593272
0.048612	0.037326541	0.1044265	0.09214167	0.1302696	0.1333216

Вектор невідомих:

W

0.025942

0.043644

0.040766

0.067916

0.030166

0.047719

Прогини плити у вузлових точках:

0.025942 м = 25,942 мм,

0.043644 м = 43,644 мм,

0.040766 м = 40,766 мм,

0.067916 м = 67,916 мм,

0.030166 м = 30,166 мм,

0.047719 м = 47,719 мм.

6. Обчислення згинальних моментів у вузлах сітки

Співвідношення для згинальних моментів та моментів кручення через прогини плити мають вигляд:

, де μ – коеффіцієнт Пуассона,

,

.

Обчислимо у вузлі 8 похідні другого порядку:

,

Згинальні моменти у вузлі 7:

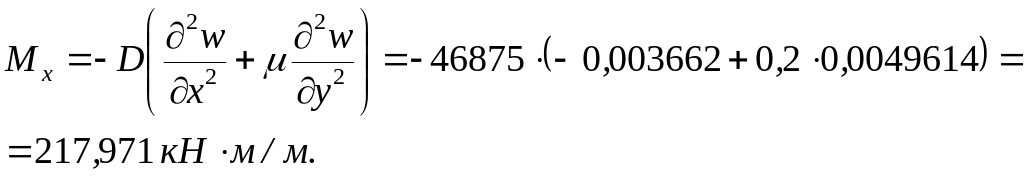
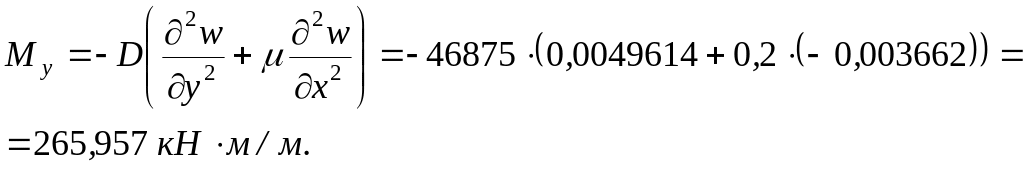
Момент кручення у вузлі 7:

Аналогічно обчислюємо згинальні моменти та моменти кручення в інших вузлах. Автоматизувати обчислення можна за допомогою електронної таблиці MS Excel. Результати цих обчислень подані у таблицях:

Таблиця згинальних моментів Мх:

Поле Mx
x/y	0	1.5	3	4.5	6
0	0.000	-216.182	-363.703	-216.182	0.000
1.5	-1080.912	217.981	818.319	217.981	-1080.912
3	-1698.573	389.585	1316.554	389.585	-1698.573
4.5	-1256.912	344.295	846.044	344.295	-1256.912
6	0.000	0.000	0.000	0.000	0.000

Таблиця згинальних моментів Му:

Поле My
x/y	0	1.5	3	4.5	6
0	0.000	-1080.912	-1818.513	-1080.912	0.000
1.5	-216.182	265.957	551.113	265.957	-216.182
3	-339.715	586.391	1152.694	586.391	-339.715
4.5	-251.382	460.179	719.638	460.179	-251.382
6	0.000	0.000	0.000	0.000	0.000

Таблиця моментів кручення Мху:

Поле Mxy
x/y	0	1.5	3	4.5	6
0	0.000	0.000	0.000	0.000	0.000
1.5	0.000	282.984	0.000	-282.984	0.000
3	0.000	16.977	0.000	-16.977	0.000
4.5	0.000	-282.984	0.000	282.984	0.000
6	0.000	-397.657	0.000	397.657	0.000

7. Побудова епюр згинальних моментів та моментів кручення

Нижче побудовані епюри згинальних моментів та моментів кручення.

Епюра згинальних моментів Мх:

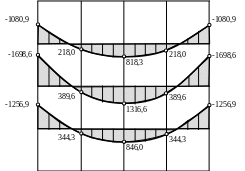
Епюра згинальних моментів Му:

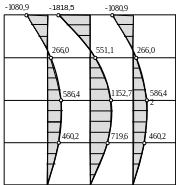
Епюра моментів кручення Мху:

8. Визначення напружень

Визначаємо напруження в крайніх фібрах плити в точці х = 3 м, у = 3 м.

9. Побудова поверхні функції прогинів плити

Використовуючи табличний процесор MS Excel, побудуємо поверхню функції прогинів плити.

Література

1. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. М.: – Высшая школа, 1990.

2. Жемочкин Б.Н. Теория упругости. М.: – Государственное издательство литературы по строительству и архитектуре, 1957.

3. Самуль В.И. Основы теории упругости и пластичности.  М.: Высшая школа, 1982.

4. Безухов Н.И. Основы теории упругости, пластичности и ползучести. М.: – Высшая школа, 1990.

5. Методичні вказівки та контрольні завдання до виконання розрахунково-графічної роботи на тему «Розрахунок тонкої плити методом скінченних різниць» із дисципліни «Будівельна механіка. Спецкурс» для студентів напряму підготовки 6.060101 «Будівництво» освітньо-кваліфікаційного рівня «бакалавр». – Полтава: ПолтНТУ, 2010. – 25 с.

6. Методичні вказівки Застосування методу скінченних різниць до розв’язання інженерних задач для студентів денної форми навчання. / Полтава: ПолтІСІ. Укладачі: О.О.Козир, О.І.Корх, Л.Ф. Крещенко, М.Є.Рогоза.