Граф Кенига

Любому гиперграфу H может соответствовать так называемый граф Кенига G = {E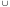 V, U}. Это двудольный граф, состоящий из двух подмножеств вершин E и V, где E – множество вершин гиперграфа, а V – множество его рёбер. Подмножества E и V являются подмножествами несмежных вершин, т.е. между их элементами нет связей (рёбер). Вершины же e_iєE и V_jєV смежные только тогда, когда в гиперграфе вершина e_i принадлежит ребру V_j. Для схемы с рис. 2.2 двудольный граф имеет вид (рис. 2.7).

e₀V₁, V₂, V₅, V₆;

e₁V₁, V₂, V₃;

e₂V₃, V₄, V₅, V₆;

e₃V₂, V₃, V₄, V₆;

e₄ V₄, V₆;

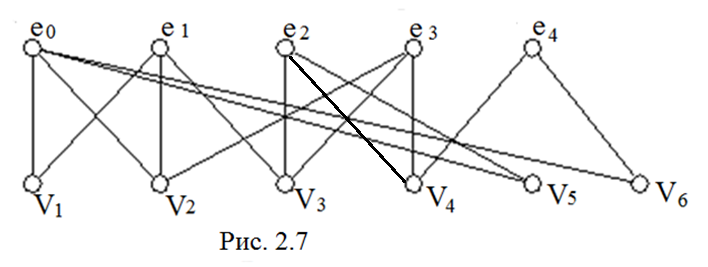
Взвешенный граф схемы

Ч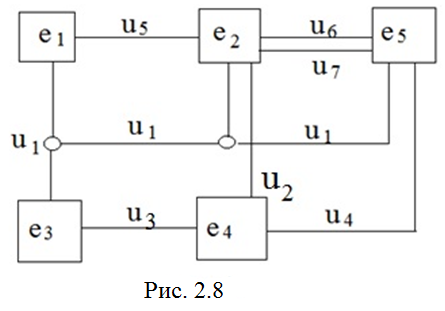 аще других используется более простое представление электрической схемы, когда элементам схемы соответствуют вершины графа eєE , а электрические цепи представляются рёбрами uєU. Пусть схема имеет вид рис. 2.8:

В таком графе каждый узел, т.е. сложная цепь, соединяющая три и более элемента, представляется полным графом с числом рёбер n(n-1)/2, где n - число элементов цепи (рис. 2.9).

Т.е. каждый элементный комплекс в ГЭК представляется полным графом.

U₁={e₁,e₂,e_3,e₅} U₂={e₂,e₄} U₃={e₃,e₄}

U₄={e₄,e₅} U₅={e₁,e₂} U₆={e₂,e₅} U₇={e₅,e₂}

Д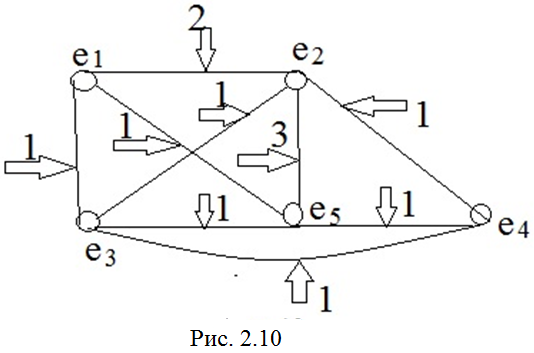 алее перейдём от полученного мультиграфа к взвешенному графу, приписав каждому ему ребру u_ij «вес» z_ij, равный числу элементарных соединений между вершинами e_i и e_j . Получим взвешенный граф схемы (ВГС) (рис. 2.10).

Взвешенный граф схемы может теперь быть описан с помощью матрицы смежности R =║r_ij║_nxn, строки и столбцы которой соответствуют вершинам ВГС.

В нашем случае:

R=		e1	e2	e3	e4	e5
	e1	0	2	1	0	1
	e2	2	0	1	1	3
	e3	1	1	0	1	1
	e4	0	1	1	0	1
	e5	1	3	1	1	0

Представление сложных цепей полным графом вносит избыточность информации, т.к. в действительности элементы соединяются в виде дерева.

М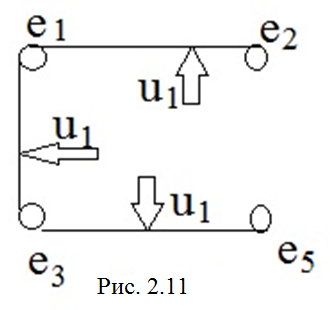 одификацией мультиграфовой модели и ВГС является модель, представляемая графом, в котором полные подграфы, моделирующие цепи u  U, заменяются покрывающими их деревьями. Такая модель проще, но сложностью является выбор одного из n^n-2 покрывающих деревьев, для каждого полного графа. Например, для цепи U₁, можно выбрать такое дерево - рис. 2.11.

Применение гкс, гэк, вгс

ГКС – является наиболее полным и точным описанием и входит в исходную информацию САПР. Непосредственно используется при решении задачи трассировки. ГКС применяется для решения задачи размещения, когда надо учитывать размеры элементов и положения их выводов. Можно для размещения сначала использовать модели ГЭК и ВГС, а для получения окончательного решения ГЭК и ГКС. Для решения задач компоновки информация о точном расположении выводов на элементах не требуется. Поэтому наиболее часто используется ВГС и ГЭК. Причём ГЭК более соответствует физическому содержанию, а ВГС при описании его матрицей смежности наиболее легко реализуется на компьютере.