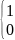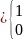Лекция 2 Формальное описание коммутационных схем

Речь идет об описании принципиальных электрических схем. В литературе по САПР принципиальные электрические схемы называют коммутационными. Связи в схеме соответствуют передаче электрических сигналов.

Принципиальную электрическую схему рассматриваем, как состоящую из множества элементов E=e₁,e₂,…,e_n, соединенных между собой электрическими цепями из множества V=v₁,v₂,…,v_m). Назовем такое представление коммутационной схемой (рис. 2.1).

К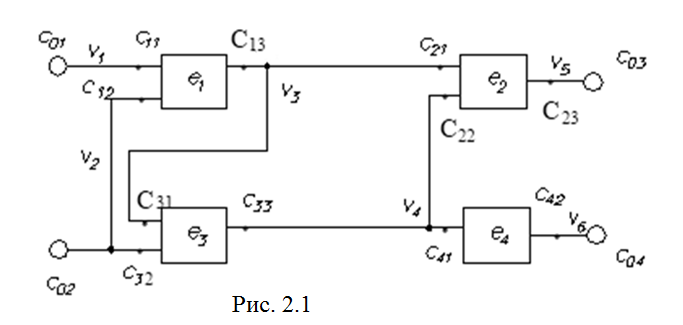 аждый i-ый элемент имеет множество выводов С=с_i1,с_i2,…,c_ik. Внешние выводы схемы, служащие для связи с другими схемами (например, через электросоединитель), удобно представить фиктивным элементом e₀.

Граф коммутационной схемы

Среди различных вариантов описания коммутационных схем наибольшей общностью и наглядностью обладает описание схемы в виде графа. Оно позволяет в целом ряде случаев найти адекватные задачи в теории графов и воспользоваться при разработке алгоритмов решения задач конструирования известными математическими методами.

Наиболее общим способом описания схем графами является граф коммутационной схемы (ГКС) G = (E,V,C,F,W).

Он несколько отличается от обычного линейного графа. Он содержит три типа вершин соответствующих:

• E – элементам;

• C – выводам элементов;

• V – цепям (комплексам).

Рёбра делятся на:

• элементные F;

• cигнальные W.

Элементные рёбра F определяют принадлежность выводов из множества C элементам из множества E и задаются парами вершин (e_i,c_k).

Сигнальные ребра W определяют вхождение выводов из С в отдельные цепи и описываются парами вершин(c_k,v_i).

Для схемы, приведенной на рис. 2.1, (ГКС) приведен на рис. 2.2.

О писание гкс матрицами

Т.к. ГКС содержит вершины и рёбра разных типов, его удобно описать двумя матрицами A и B.

Матрица A представляет цепи схемы и определяется следующим образом: А=║a_ij║_mxk, где m - число цепей, k - число выводов в схеме. Строки матрицы соответствуют цепям, а столбцы – выводам элементов.

Элемент матрицы

aij=	если вывод сi принадлежит цепи vj в противном случае

Для графа, приведенного на рис. 2.2, матрица А имеет вид:

A=		c01	c02	c03	c04	c11	c12	c13	c21	c22	c23	c31	c32	c33	c41	c42
	v1	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0
	v2	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0
	v3	0	0	0	0	0	0	1	1	0	0	1	0	0	0	0
	v4	0	0	0	0	0	0	0	0	1	0	0	0	1	1	0
	v5	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0
	v6	0	0	0	1	0	0	0	0	0	0	0	0	0	0	1

Каждый столбец матрицы A содержит одну единицу, поскольку любой вывод может входить лишь в одну цепь. Число единиц в любой строке матрицы равно размеру соответствующей цепи.

Матрица B=║b_ij║_nxk, выделяет подмножества выводов, принадлежащих отдельным элементам. Строки матрицы соответствуют элементам, а столбцы – выводам.

Элемент матрицы

bij	если вывод сj принадлежит элементу еi; в противном случае

Для графа, приведенного на рис. 2.2, матрица B имеет вид:

B=		c01	c02	c03	c04	c11	c12	c13	c21	c22	c23	c31	c32	c33	c41	c42
	e0	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0
	e1	0	0	0	0	1	1	1	0	0	0	0	0	0	0	0
	e2	0	0	0	0	0	0	0	1	1	1	0	0	0	0	0
	e3	0	0	0	0	0	0	0	0	0	0	1	1	1	0	0
	e4	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1

В каждом столбце матрицы В одна единица, т.к. вывод может принадлежать только одному элементу. Число единиц в строке равно числу выводов на соответствующем элементе.

Структуру ГКС можно задать одной матрицей T=║t_ij║_nxk1, строки которой соответствуют элементам, а столбцы выводам элемента, причём к₁ = max k_i, i=1,n.

Элемент матрицы t_ij представляет номер цепи, связанной с выводом c_j элемента e_i. Т.е. t₂₃ – номер цепи, связанной с выводом c₃ элемента e₂. Для нашей схемы:

T=		c1	c2	c3	c4
	e0	1	2	5	6
	e1	1	2	3	-
	e2	3	4	5	-
	e3	3	2	4	-
	e4	4	6	-	-

Матрица T называется матрицей цепей. Для построения матрицы цепей необходимо каждой цепи присвоить номер.

Существуют упрощенные модели схем. Так, при компоновке элементов в конструктивные узлы можно не рассматривать выводы элементов, а рассматривать только сами элементы. Тогда элементные рёбра можно устранить, т.е. вершины - как бы «стянуть» в элементы (убираем выводы элементов, а цепи обозначаем точками). Тогда можно построить граф элементных комплексов (ГЭК) G¹= (E,V¹,W) Здесь множества вершин соответствуют:

• Е - элементам;

• V¹ - элементным комплексам;

• W - сигнальным рёбрам.

Элементный комплекс V'_j - подмножество элементов из E=e₁,e₂,…,e_n, соединенных цепью j, j=1,M. Элементные комплексы могут содержать общие элементы, то есть V'_jV'_j0, ij. Число элементов в комплексе V'_j назовем размером элементного комплекса p'_j.

Г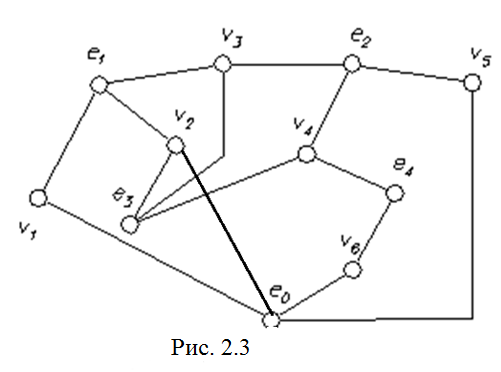 ЭК для схемы рис. 2.2 имеет вид:

Описать множества цепей (комплексов) этого графа

V₁=e₀,e₁; V₂=  ; V₃= ; V₄= ; V₅= ; V₆= 

Для описания ГЭК удобно воспользоваться матрицей Q=║q_ij║_nxm, строки которой соответствуют элементам, а столбцы элементным комплексам:

qij	, если элемент еi принадлежит цепи vj1 (связан с ней); в противном случае

В нашем случае:

Q=		V11	V21	V31	V41	V51	V61
	e0	1	1	0	0	1	1
	e1	1	1	1	0	0	0
	e2	0	0	1	1	1	0
	e3	0	1	1	1	0	0
	e4	0	0	0	1	0	1