30. Эксцесс есть степень крутости эмпирического распределения по отношению к нормальному. Он определяется по формуле:

где числитель — центральный момент четвертого порядка

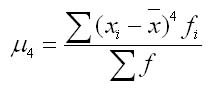
Когда распределение островершинное по отношению к нормальному, эксцесс будет положительным, если плосковершинное — отрицательным. Для нормального распределения Е = 0.

Если частоты убывают слева и справа от центра распределения с разной скоростью, то такие распределения называют асимметричными. Для характеристики степени асимметрии двух или нескольких рядов пользуются коэффициентом асимметрии.

Для одновершинных распределений:

Более точным является коэффициент асимметрии, рассчитанный как отношение центрального момента третьего порядка (μ³) к среднеквадратическому отклонению в 3-й степени (Ϭ³):

31. Показатели вариации.

Для оценки надежности качества средней используют показатели вариации, с помощью которых можно определить меру вариации и выяснить причины, вызывающие вариацию признаков.

Измерение вариации имеет важное теоретическое и практическое значения. С помощью показателей вариации можно охарактеризовать однородность совокупности, планомерность многих процессов распределения.

В теоретическом плане, показатели вариации дают представление об этапах развития. С практической точки зрения, показатели вариации являются отправным пунктом для оценки имеющихся явлений и позволяют оценить типичность средней величины.

Для измерения набора вариации, в статистике используют системы абсолютных и относительных показателей.

Для оценки качества средней, используются показатели меры и степени колеблемости.

Меры колеблемости:

1. Размах вариации:

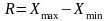
2. Среднее линейное отклонение:

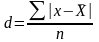
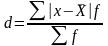
3. Среднее квадратичное отклонение:

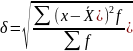
Устойчивость распределения 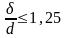, тогда распределение устойчивое.

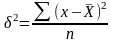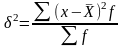4. Дисперсия: - простая - взвешенная

Дисперсия имеет самостоятельное аналитическое значение

32. Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения. Цель его - выявление основных свойств и закономерностей стат. совокупности.

Различают два типа рядов распределения:

атрибутивный;

вариационный.

Ряды распределения, построенные по качественным признакам, называют атрибутивными. (Например, распределение население по полу, характеру труда, национальности и т.д.)

Ряды распределения, построенные по количественному признаку называются вариационными. Числовые значения признака - вариантами.

Например, себестоимость 1 кВт/ч электроэнергии по различным тепловым станциям:

Здесь представлены четыре варианты признака в пределах от 0,58 до 0,67 руб. Колебания себестоимости 1 кВт/ч электроэнергии на различных ТЭЦ обусловлены различными факторами, часто действующими в противоположных направлениях (например, снижение уд. расхода топлива ведёт к снижению себестоимости 1 кВт/ч, а повышение цен на топливо - к увеличению себестоимости). В результате совместного действия многих факторов складывается величина собственности 1 кВт/ч на отдельных ТЭЦ.

Изучение характера и степени вариации признаков и отдельных единиц совокупности является важнейшим вопросом всякого статистического исследования. Данные о стоимости 1 кВт. ч электроэнергии по 5 ТЭЦ образуют так называемый первичный ряд. При наличии достаточно большого количества вариантов значений признака первичный ряд становится труднообозримым и непосредственное рассмотрение его не дает представления о распределении единиц по величине признака в совокупности. Первым шагом в упорядочении первичного ряда является его ранжирование, т.е. расположение всех вариантов ряда в возрастающем (или убывающем) порядке x₁ x₂… x_i… x_n.

вариационный распределение колеблемость ряд

Рассматривая первичный ряд можно видеть, что варианты признака у отдельных единиц совокупности повторяются.

Число повторений отдельных вариантов называют частотой (обозначим ѓ)

Сумма частот, равная объему изучаемой совокупности - n.

По характеру вариации различают дискретные и непрерывные признаки.

Дискретные признаки отличаются друг от друга на некоторую конечную величину, т.е. даны в виде конкретных чисел. (Например, число детей в семье).

Непрерывные признаки могут отличаться друг от друга на сколь угодно малую величину и в определенных границах принимать любые значения. Например, зарплата рабочих, % выполнения.

Способы построения вариационного ряда для этих видов признаков различны. Для построения дискретного ряда с небольшим числом вариантов достаточно перечислить все встречающиеся варианты значений признака (x_i), а затем подсчитать частоту повторений каждого варианта ѓ_{i. (}Например, распределение студентов по успеваемости и т.п.)

Ряд распределения принято оформлять в виде таблицы.

33.С помощью дисперсионного анализа создается возможность выявить влияние факторов положенных в основу группировки на результат и оценить меру этого влияния .Такой анализ возможно осущ-ть различными методами( в частн. Корреляционым) В основе дисперсн-го анализа лежит несколько различных видов дисперсий. 1)Общая дисперсия: в своей величине улавливает влияние всех факторов и факторов положенных в основу группировки и факторов случайных находящихся за пределами группировочного признака.Ϭ²=∑(х-ẋ)²/n( по несгруппированым данным) ;Ϭ²=∑(х-ẋ)²•f/∑•f ( по сгруппированным данным).2) Межгрупповая дисперсия : улавливает влияние фактора положенного в основе группировки,т.е систематического фактора.δ²=∑(ẋ_i-ẋ)²•f_i/∑f_i,где ẋ_i- средняя групповая ẋ- общая средн. По всей совокупности.3) Средняя внутригруповая дисперсия :улавливает влияние случайных величин.Ϭ² =∑Ϭ²_i •f_i/∑f_i 4) Частная дисперсия Ϭ²_iраситывается по каждой группе ,Ϭ²_i =∑(x_i-ẋ)²/n Правило сложений дисперсий:

Для проведения факторного анализа возможно использование различных видов дисперсий:

1. Общая: - простая - взвешенная Общая дисперсия улавливает влияние группы факторов:

   1. Положенного в основу группировки – систематический фактор;

   2. Случайной причины – оказывающей влияние на результат.

Таким образом, с помощью дисперсионного анализа можно выявить влияние систематического фактора и случайных величин на результат, а также оценить тесноту связи между фактором, положенным в основу группировки и результатом.

2. Межгрупповая дисперсия: выражает величину, обусловленную влиянием признака, положенного в основу группировки, выражает влияние систематического фактора.

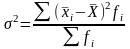, где: 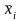- среднее значение факторного признака, положенного в основу группировки по отдельно взятой группе;

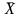- среднее значение факторного признака в целом по совокупности;

-частота повторения в соответствующей группе.

3. Средняя внутригрупповая дисперсия – устанавливает влияние случайных величин.

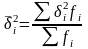- внутригрупповая дисперсия

- средняя внутригрупповая дисперсия