2.3. Минимизация по методу Квайна–Мак-Класки

Одним из наиболее популярных способов минимизации расчетно-табличных методов является алгоритм Квайна с модификацией Мак-Класки. Алгоритм разделяется на ряд этапов, для понимания которых надо ввести некоторые определения. Каждая БФ как было определено в п. 1.8, может быть представлена единственной совершенной нормальной формой (ДСНФ или КСНФ). Но булевы функции могут быть представлены и другими дизъюнктивными (конъюктивными) нормальными формами, имеющими меньшее количество букв, а значит более простыми схемами.

Определение 2.4. Функция входит в функцию , если она принимает значения равные нулю на тех же наборах, что и функция . Вхождение функции записывают .

Пример 2.3. Пусть функции и заданы таблицей истинности (табл. 2.3). Пусть функция , где - часть функции . Она входит в функцию .

Таблица 2.3. К примеру 2.3

0	0	0	0	0	0	0	0	1
0	0	1	1	1	1	1	1	1
0	1	0	0	0	0	0	0	1
0	1	1	1	0	0	1	1	1
1	0	0	0	0	0	0	0	0
1	0	1	0	0	1	0	1	0
1	1	0	1	0	0	0	0	0
1	1	1	0	0	0	0	1	0

Определение 2.5. Функция, являющаяся элементарной конъюнкцией (дизъюнкцией) и входящая в данную функцию, называется импликантой.

Определение 2.6. Простой импликантой называется импликанта, которая входит в данную функцию, но никакая собственная часть ее в функцию не входит. Если выделить собственную часть функции , то по таблице 2.3 она не входит в функцию из-за набора 101, т.е. не является импликантой.

Проверка собственной части функции показывает, что она импликанта. Но простая ли она? Ее собственные части и не входят в функцию . Это видно из таблицы 2.3. Следовательно, простая импликанта. Простые импликанты – самые короткие элементарные конъюнкции (дизъюнкции), входящие в данную функцию.

Определение 2.7. Дизъюнкция всех простых импликант называется сокращенной ДНФ (КНФ). Из сокращенных НФ нельзя выбросить буквы, но можно исключить некоторые импликанты.

Определение 2.8. Если из сокращенной НФ исключить все “лишние” импликанты, то получится тупиковая ДНФ (ТДНФ, ТКНФ), которых может быть несколько.

Определение 2.9. Тупиковая ДНФ (КНФ), содержащая наименьшее число букв, называется минимальной ДНФ (КНФ). Их тоже может быть несколько.

Определение 2.10. Тупиковая НФ, содержащая наименьшее число членов, называется кратчайшей НФ. В общем случае минимальные и кратчайшие НФ могут не совпадать.

Рис. 2.7. Блок-схема алгоритма минимизации

Таким образом, на заключительном этапе минимизация может распадаться на два варианта, которые называют факторизацией и определяются только перебором вариантов.

Общий алгоритм минимизации можно изобразить укрупненной блок-схемой (рис. 2.7), этапы которого представляются следующим образом:

1. Если функция задана таблицей истинности, то представляем ее в виде ДСНФ или КСНФ по п. 1.8.

Если функция задана в произвольном базисе, то ее надо привести к базису {И, ИЛИ, НЕ}, раскрыть групповые отрицания по формулам Де Моргана и развернуть полученную ДНФ (КНФ) до ДСНФ (КСНФ) (пример 1.6).

2. Применяя законы склеивания и поглощения, найти сокращенную ДНФ (КНФ).

3. Исключая лишние импликанты, найти множество тупиковых форм.

4. Перебором тупиковых НФ найти минимальные или кратчайшие нормальные формы.

5. Перейти к скобочным формам (СФ), если это уменьшит количество букв.

Минимизация по числу букв примерно соответствует минимуму числа входов логических элементов, а минимизация по числу членов – минимуму функциональных элементов.

Методы Квайна и Мак-Класки отличаются только на этапе нахождения сокращенных нормальных форм.

Рассмотрим минимизацию на примере.

Пример 2.4. Минимизировать функцию, заданную числовым способом , которая принимает значение 1 на 10 наборах. Найти сокращенную ДНФ по методу Квайна.

Решение. Процесс минимизации удобно выполнить в таблице (табл. 2.4). В первый столбец таблицы запишем ДСНФ в виде набора конституент единицы для заданной функции. Если в совершенной нормальной форме БФ провести все возможные операции склеивания и поглощения, то можно получить сокращенную ДНФ (КНФ), т.е. дизъюнкцию (конъюнкцию) всех ее простых импликант (теорема Квайна).

Напомним операции склеивания и поглощения:

; - склеивание.

; - поглощение.

Обратимся к табл. 2.4. Будем проверять возможность склеивания 1-го члена в 1-м столбце со всеми остальными, затем 2-го члена с остальными и т.д. Результаты склеивания будем записывать в столбец 2. В столбце 1 отмечаем (звездочками, птичками) склеивающиеся члены. В столбце 2 указываем, какие строки столбца 1 участвовали в склеивании. Эти отметки необходимы для самоконтроля с целью обнаружения ошибок на каждом этапе. В табл. 2.4 показано, что пропущенная склейка строк (3-5) первого столбца при втором просмотре обнаружена и записана в последнюю 11-ю строку, так как порядок записи склеек значения не имеет, а вот необнаруженная склейка даст неверный результат.

Таблица 2.4. Получение сокращенной ДНФ по методу Квайна

№	1	2	3
1	*	* (1-2)	(1-8)
2	*	(1-4)	(3-5)
3	*	* (1-6)
4	*	(2-3)
5	*	* (2-8)
6	*	(5-10)
7	*	(6-7)
8	*	* (6-8)
9	*	(8-9)
10	*	(9-10)
11		(3-5)

Конъюнкции 2-го столбца имеют ранг (n-1). Повторяем склеивание для второго столбца, результат записываем в 3-й столбец и т.д. пока склеивания возможны.

Примечание. При склеивании конъюнкций (n-1) –го, (n-2) –го ранга и т.д. следует рассматривать только члены с одинаковыми номерами переменных.

Выполняем поглощения. Все отмеченные конъюнкции будут поглощены, а оставшиеся представляют собой простые импликанты. Дизъюнкция всех простых импликант есть сокращенная ДНФ.

Проделаем указанные действия для заданной функции с занесением результатов в столбцы табл. 2.4. Анализируем результаты. В первом столбце все строки помечены. Значит, все члены с четырьмя переменными в решение не войдут. Во втором столбце не помечены 7 строк. Включаем их в решение. В 3-м столбце имеются две одинаковые импликанты. По закону тавтологии оставляем только одну. Итак, сокращенная ДНФ будет иметь 8 членов:

(2.10)

Порядок записи импликант также не имеет значения.

Алгоритм Мак-Класки отличается незначительно от алгоритма Квайна:

1. Исходные наборы записываются не в виде конъюнкций переменных, а в виде двоичных кодов, где записываются как 1,а - как 0.

2. Все множество наборов, на которых функция принимает значения, равные единице, разбивается на группы, в каждую из которых включаются наборы из единиц. При переменных число групп не может превышать .

3. Склеивание производится только между соседними группами. Склеивающиеся наборы также помечаются. Выпавшие переменные помечаются как или черточками. В решение включаются наборы, не участвовавшие в склеивании.

Пример 2.5. Найти сокращенную ДНФ для функции, заданной в примере 2.4 по методу Мак-Класки.

Решение.

Переводим заданную функцию в двоичные наборы, разбиваем на группы с одинаковым числом единиц в каждой группе и заполняем таблицу 2.5. В первом столбце будут располагаться наборы кубического комплекса . Во втором наборы комплекса и т.д. пока множество кубов не будет пустым.

В результате склеиваний получилась сокращенная ДНФ, которую можно записать в виде дизъюнкций двоичных кодов или перейти к переменным, как в методе Квайна:

(2.11)

Таблица 2.5.

Поиск сокращенной ДНФ по методу Мак-Класки

№
1	* 0 гр		(1-7)
2	1 гр		(3-5)
3
4
5	2 гр
6
7
8	3 гр
9
10	* 4 гр
11

Переходя к переменным, получим тот же результат, что и в выражении (2.10) по методу Квайна, только с другим порядком следования членов сокращенной ДНФ, что несущественно.

Поиск тупиковых форм БФ можно осуществить методом испытания импликант или методом импликантных матриц (таблиц покрытий).

Метод испытания импликант заключается в поочередном вычеркивании каждой импликанты из сокращенной ДНФ с подстановкой в оставшееся выражение таких значений переменных, которые обращают исключенную импликанту в 1. Если оставшееся выражение будет тождественно равно 1, то испытываемая импликанта лишняя. Метод испытания импликант неудобен в практической реализации и может использоваться при небольшом числе переменных.

Метод импликантных матриц (таблиц покрытий) заключается в составлении матрицы, строками которой являются простые импликанты сокращенной НФ, а столбцами – конституенты единицы (минтермы) данной функции при минимизации в ДНФ или конституенты нуля (макстермы) при минимизации в КНФ. Обработка матрицы (таблицы покрытий) состоит из следующих этапов:

1. Расстановка меток.

Если в некоторые конституенты 1 (или 0) входит данная импликанта (говорят, что она покрывает данные столбцы, отсюда и название – таблица покрытий), то на пересечении строки и столбцов ставится метка. Количество меток в строках при минимизации полностью определенных функций строго определено: если число переменных в столбцах равно , а в какой-то строке содержится переменных, то число меток в строке должно быть равно , где равно числу исключенных букв. Значит, если в строке число букв меньше на две, чем в столбцах, то число меток должно быть , при - две, при - одна метка. Если это условие не выполняется, то сокращенная НФ неверна и надо вернуться к первому этапу минимизации.

2. Нахождение существенных импликант.

Если в столбце содержится только одна метка, то импликанта, стоящая в соответствующей строке, называется существенной импликантой. Она обязательно войдет во все тупиковые формы функций, образующих минимальное покрытие. По другой терминологии существенные импликанты называют экстремалями. Множество существенных импликант (экстремалей) образует ядро покрытия функции.

3. Вычеркивание лишних столбцов.

Если в таблице имеются существенные импликанты, то из таблицы можно вычеркнуть столбцы, покрываемые этими импликантами. Если в таблице, полученной после выделения существенных импликант, окажутся два столбца, имеющие метки в одинаковых строках, то один из столбцов вычеркивается.

4. Вычеркивание лишних простых импликант.

Если после вычеркивания столбцов в таблице появляются строки, не содержащие меток, то импликанты, соответствующие таким строкам, вычеркиваются.

5. Выбор минимального покрытия.

В таблице, полученной после выделения ядра покрытия, выбирается совокупность простых импликант, обеспечивающая покрытия всех оставшихся столбцов с минимальной ценой. Другими словами, оставшиеся непокрытыми столбцы нужно покрыть наименьшим числом наиболее коротких импликант.

Примечание.

1. Число минимальных покрытий может иметь несколько вариантов.

2. Функция может не иметь существенных импликант. В этом случае, обработка покрытий отличается от приведенной выше и будет рассмотрена дальше.

3. Таблица покрытий может обрабатываться как по сокращенным формам, так и в виде Мак-Класки.

Пример 2.6. Найти минимальное покрытие для функции, заданной в примере 2.5.

Решение. Строим таблицу покрытий. Ее столбцами будут 10 конституент единиц функции, а строками - простые импликанты, найденные в примере 2.5.

Таблица 2.6. Таблица покрытий для примера 2.5.

В таблице 2.6 введен столбец для буквенного обозначения строк с целью удобства обращения к ним, например, вместо строки проще сказать строка . С этой же целью пронумерованы столбцы.

Расставим метки в строках и убедимся, что количество меток соответствует правилам. Действительно, в последней строке имеются четыре метки, а в остальных строках по две.

Находим существенные импликанты. По одной метке содержится в 4-м и 7-м столбцах, значит, в строках - и - находятся существенные импликанты (экстремали), образующие ядро покрытия.

Вычеркиваем столбцы 1, 4, 6, 7, как покрываемые этими импликантами. Лишних простых импликант после вычеркивания столбцов в данном примере нет. В результате получим сокращенный вариант таблицы покрытий (табл. 2.7).

Выбираем минимальное покрытие. Оно будет состоять из ядра покрытия плюс минимальное число самых коротких импликант, покрывающих невычеркнутые столбцы. Здесь возможны варианты покрытий. Например, можно взять строку , она покроет 2-й и 3-й столбцы, строку (покроет 8-й и 9-й столбцы) и строку (покроет 5-й и 10-й столбцы). Все столбцы табл. 2.7 будут покрыты. Включив в решение ядро покрытия, получим вариант минимального покрытия в кодах.

Таблица 2.7. Сокращенная таблица покрытий

Простые импликанты	0010	0011	0111	1010	1110	1111
	2	3	5	8	9	10

, (2.12)

. (2.12а)

В формулах (2.12, 2.12а) пунктиром отделено ядро покрытия.

Возможны и другие варианты покрытия, например, строкой , строкой , строкой , что в переменных дает выражение:

. (2.13)

Сравним выражения (2.12) и (2.13) по количеству членов и количеству букв. По числу членов оба варианта одинаковы (5 членов), т.е. при минимизации в классе кратчайших форм и равноценны. По числу букв, входящих в покрытия при минимизации в классе минимальных форм, функция предпочтительнее, так как содержит на одну букву меньше (14 букв).

По формулам (2.12), (2.13) можно построить логические схемы, реализующие эти функции. Проследим, как менялась сложность схемы на каждом этапе. Найдем расчетную цену по Квайну:

Здесь при расчете учтено, что сокращенная ДНФ имеет 7 трехбуквенных импликант и одну двухбуквенную (всего 8 импликант). Наконец, для выражения 2.13 цена по Квайну будет равна:

Как видим, цена по Квайну уменьшилась более чем в два раза. Отсюда можно сделать вывод, что уметь минимизировать все-таки полезно. Конечно, не все БФ минимизируются одинаково хорошо. Есть и такие, которые вообще не минимизируются, т.е. их можно записать только в ДСНФ. Далее мы приведем примеры таких функций.

При большем числе переменных число вариантов существенно увеличивается, что затрудняет оценки минимальных покрытий. Известен метод отыскания всех тупиковых форм заданной функции (метод Петрика), который будет рассмотрен далее.

Минимизация БФ в классе конъюнктивных нормальных форм по методу Квайна–Мак-Класски проводится по тому же алгоритму, что и для ДНФ. Исходной является КСНФ. Затем находятся сокращенная и тупиковые формы, а затем, отбирается минимальная или кратчайшая форма.

Рассмотрим минимизацию на примере.

Пример 2.7. Минимизировать в КНФ функцию, заданную в примере 2.5, и сравнить результаты минимизации.

Решение. Заданная функция равна нулю на наборах 1, 5, 6, 11, 12, 13. Запишем КСНФ этой функции, получим:

(2.17)

Найдем сокращенную форму этой функции, для этого построим таблицу 2.8.

Записываем сокращенную форму из табл. 2.8 по результатам склеиваний и поглощений.

(2.18)

Таблица 2.8. Исходная таблица в КНФ

	1	2
1		(1-2)
2		(2-5)
3		(5-6)
4
5
6

Строим импликантную матрицу (табл. 2.9) и находим тупиковые формы функции.

Таблица 2.9. Таблица покрытий в КНФ

Определяем существенные импликанты и вычеркиваем столбцы. После удаления столбцов в строке не оказывается ни одной метки, поэтому строку вычеркиваем.

В результате получаем единственную тупиковую форму, которая является также и минимальной и кратчайшей:

(2.19)

Функция содержит 4 члена, 14 букв. При сравнении этой же функции, минимизированной в ДНФ, из (2.13) видим, что число букв в обеих формах одинаково, но число членов в выражении (2.19) равно четырем, т.е. в классе кратчайших форм функция в КНФ предпочтительнее, хотя разница невелика.

Цена по Квайну:

входа (2.20)

На практике, конечно, конкретная реализация схемы зависит от применяемых типов логических элементов, числам входов в них и от других соображений, но этим примером хотелось обратить внимание на минимизацию в КНФ, которая позволяет получить хорошие результаты, хотя для начинающих проектировщиков ДНФ кажется более “привычной”. На рис. 2.8 приведена логическая схема в ДНФ, построенная по выражению 2.13.

Рис. 2.8. показывает, что даже для небольшой схемы способ непосредственного соединения входов и выходов логических элементов неудобен как с точки зрения удобства изображения, так и для анализа правильности схемы.

Рис. 2.8. Логическая схема, реализующая функцию в ДНФ

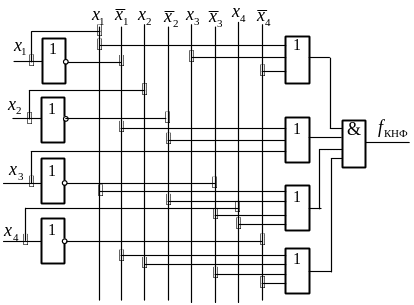
Более удобен способ с использованием шин, с которых разводятся логические переменные. На рис. 2.9 приведена схема, реализующая для КНФ формулу (2.19).

Рис. 2.9. Логическая схема, реализующая логическую функцию в КНФ

При реализации более сложных схем изображают одну шину с нумерацией входящих в нее проводников.