2. Минимизация булевых функций

2.1. Сущность и этапы минимизации бф

Реализация булевых функций по совершенным нормальным формам неэффективна из-за больших затрат на электронное воплощение функций в интегральных схемах. В этом смысле, математике (логике) “пришлось” приспосабливаться к техническим требованиям. Основным требованием при этом подходе является минимальность оборудования при наибольшем быстродействии логических схем. Требования эти могут быть противоречивыми, так как стремление создать наиболее экономичную (в смысле простоты) схему приводит к уменьшению быстродействия, и наоборот.

Количество оборудования приближенно можно определить ценой по Квайну. Существует несколько разновидностей цены.

Определение 2.1. Цена по Квайну схемы определяется числом входов логических элементов схемы

. (2.1)

Каноническая минимизация БФ обычно ведется по критерию минимального числа букв в ДНФ или КНФ, либо по критерию минимального числа членов ДНФ (КНФ).

Несколько иначе задачу минимизации рассматривают исходя из кубических представлений (п. 1.2). Кубический комплекс БФ получается объединением кубов разных размерностей, в которых координаты, обозначенные символами , называются свободными, а остальные связанными.

.

Число свободных переменных определяет размерность куба .

Определение 2.2. Множество кубов в таких, что каждая вершина включена хотя бы в один куб множества , называют покрытием комплекса (и булевой функции). Например, для функции - покрытие, которому соответствует функция .

Определение 2.3. Введем понятие цены покрытия. Цена - куба определяется как и соответствует количеству связанных переменных. Цена покрытия есть сумма всех цен кубов.

, (2.2)

где - число - кубов в покрытии. Суммирование охватывает все значения ( ).

Второй вариант цены покрытия - цена как цена , увеличенная на число кубов в покрытии :

. (2.3)

Например, покрытие имеет цены и .

Покрытие с минимальной ценой называется минимальным покрытием комплекса (БФ) в смысле цены по Квайну, а ДНФ (КНФ) определенная по минимальному покрытию, называется минимальной ДНФ (КНФ).

Способ оценки сложности схемы по суммарному количеству входов (2.1) не определяет абсолютной величины сложности схемы, но обеспечивает возможность сравнения различных вариантов схем по количеству используемого оборудования. Эта оценка сложности схем распространяется и на схемы с большим числом уровней (каскадов).

Другой возможной характеристикой логических схем является их быстродействие, которое на этапе логического проектирования может характеризоваться задержкой прохождения сигнала по самому длинному пути от входа к выходу.

Поясним это на примере. Любая реальная схема не может переключиться мгновенно (это противоречит законам физики). Задержки связаны с процессами в переходах микросхем, с наличием паразитных емкостей и индуктивностей и т.д. Анализ этих задержек изучается в дисциплинах по электронике и схемотехнике. Скажем пока только, что в справочниках по ИМС (интегральные микросхемы) содержатся цифровые данные по задержкам конкретных схем данной серии (в физических единицах).

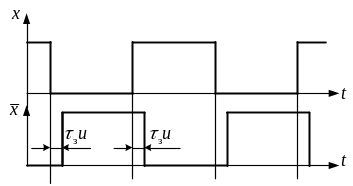
Рис. 2.1. Временные диаграммы логической схемы

При логическом синтезе можно использовать приближенную оценку быстродействия по количеству элементов схемы, через которые должен пройти двоичный сигнал на выход.

Пусть имеется инвертор, на который поступают нули и единицы в какой-то части схемы (рис. 2.1). На выходе должен быть инверсный сигнал, но он появляется с задержкой, которая обозначена как задержка на элементе . Аналогично можно ввести задержки на конъюнкторах, дизъюнкторах и других логических элементах.

Для расчетов задержек на логическом уровне можно приближенно считать их одинаковыми и обозначать как - задержка на элементе.

В этом случае общая задержка схемы будет равна сумме задержек в каждом каскаде (ярусе), т.е.

, (2.4)

где - максимальное количество каскадов (уровней) логической схемы на пути прохождения сигнала.

При построении схем по нормальным формам (ДСНФ, КСНФ) задержка не превышает (или при отсутствии инверторов в схеме). Это самая минимальная задержка в логических схемах. При других способов реализации схем задержка может быть больше. Задержка в схеме связана с максимальной частотой работы схемы соотношением . Если это неравенство не будет выполняться, то схема не будет успевать правильно обрабатывать сигналы.

На первом этапе минимизации БФ стремятся получить минимальные ДНФ (КНФ). На втором этапе пытаются получить скобочные формы (СФ) БФ для уменьшения общего числа букв в логической функции (факторизация БФ). Факторизация бывает важным приемом при реализации БФ в виде интегральных схем с ограниченным числом входов.

Способов минимизации БФ и построения оптимальных логических схем достаточно много, и каждый имеет свои преимущества и недостатки для ручной или машинной минимизации, количества переменных БФ, базиса в котором будут реализовываться схемы и т.д.

Могут применяться расчетные методы минимизации на основе преобразования исходной функции по законам булевой алгебры, использование расчетно-табличных методов (методы Квайна-Мак-Класки, Блока-Порецкого, Нельсона). Такие методы как неопределенных коэффициентов, минимизирующих карт в пособии не рассматриваются, как имеющие уже только исторический интерес. Для небольшого числа переменных успешно применяются табличные методы по картам Вейча-Карно.

С внедрением автоматизированного синтеза логических схем распространение получили алгебраические методы, такие как метод К. Рота (алгоритм извлечения), позволяющие формализовать действия на всех этапах минимизации функции до получения минимальных форм.