Связь со скоростью и нормальным ускорением

Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории точки. При этом существует связь между величиной скорости  , нормальным ускорением   и радиусом кривизны траектории   в данной точке:

путем называют длину траектории, по которой движется тело. Перемеще́ние (в кинематике) — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта.

Вопрос 19 какое движение называют равномерным? Каковы его свойства?

Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени проходит одинаковое расстояние. Равномерное движение материальной точки — это движение, при котором величина скорости точки остаётся неизменной. Расстояние, пройденное точкой за время  , задаётся в этом случае формулой  . Равномерное Прямолинейное движение — это движение, при котором тело (точка) за любые равные и бесконечно малые промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости и времени.

.

Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты   точки от времени является линейной:

,

где   — начальная координата точки,   — проекция вектора скорости на координатную ось.

По определению инерциальной системы отсчёта, точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если векторная сумма всех сил, приложенных к точке, равна нулю.

При равномерном движении точки по окружности её траекторией является дуга. Точка движется с постоянной угловой скоростью  , а зависимость угла поворота точки от времени является линейной:

,

где   — начальное значение угла поворота.

Эта же формула определяет угол поворота абсолютно твёрдого тела при его равномерном вращении вокруг неподвижной оси, то есть при вращении с постоянной угловой скоростью  .

Важной характеристикой данного типа движения является линейная скорость материальной точки 

Нужно помнить, что равномерное движение по окружности — движение равноускоренное. Хотя модуль линейной скорости и не меняется, но меняется направление вектора линейной скорости (из-за нормального ускорения).

Вопрос 20 Какое движение называют равноускоренным? Равнозамедленным? Ускорением a называется отношение изменения скорости тела к малому промежутку времени, за который это изменение произошло[1]  . Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению. Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения. Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

21) Что называют тангенциальным ускорением, нормальным, полным. Приведите примеры. Тангенциа́льное ускоре́ние  — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости в отличие от нормальной компоненты, характеризующей изменение направления скорости. Тангенциальное ускорение равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени. Таким образом, направлено в ту же сторону, что и вектор скорости при ускоренном движении (положительная производная) и в противоположную при замедленном (отрицательная производная).

где   — путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.

Абсолютная величина тангенциального ускорения зависит только от путевого ускорения, совпадая с его абсолютной величиной, в отличие от абсолютной величины нормального ускорения, которая от путевого ускорения не зависит, зато зависит от путевой скорости

Центростремительное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.

Наиболее простым примером центростремительного ускорения является вектор ускорения при равномерном движении по окружности (направленный к центру окружности).

В классической механике центростремительное ускорение вызывается компонентами сил, направленными ортогонально вектору скорости, и, следовательно, оно перпендикулярно касательной к траектории в данной точке. Например, кривизна орбит космических объектов характеризуется центростремительным ускорением, вызванным гравитацией.

Связанное понятие для неинерциальных систем отсчёта — центробежная сила.

Первым правильные формулы для центростремительного ускорения (или центробежной силы) получил, по-видимому, Гюйгенс. Практически с этого времени рассмотрение центростремительного ускорения входит в обычную технику решения механических задач и т.д.

Несколько позже эти формулы сыграли существенную роль в открытии закона всемирного тяготения (формула центростремительного ускорения использовалась для получения закона зависимости гравитационной силы от расстояния до источника гравитации, исходя из выведенного из наблюдений третьего закона Кеплера).

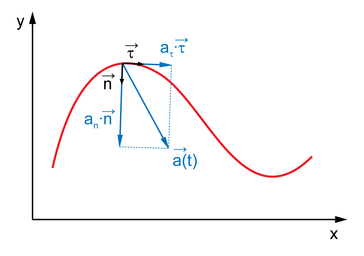
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):

Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав­ляющая ускорения —быстроту изменения скорости по направлению (направлена к цен­тру кривизны траектории).

. 22) Радиус кривизны траектории — это радиус окружности R, по которой в этот момент движется тело.

23) Принцип суперпозиции является следствием, прямо вытекающим из рассматриваемой теории, а вовсе не постулатом, вносимым в теорию a priori. Так, например, в электростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.

Другим следствием линейности уравнений Максвелла является тот факт, что лучи света не рассеиваются и вообще никак не взаимодействуют друг с другом. Этот закон можно условно назватьпринципом суперпозиции в оптике.

Подчеркнём, что электродинамический принцип суперпозиции не есть незыблемый закон Природы, а является всего лишь следствием линейности уравнений Максвелла, то есть уравнений классической электродинамики. Поэтому, когда мы выходим за пределы применимости классической электродинамики, вполне стоит ожидать нарушение принципа суперпозиции.

24) В 1960 г. Данциг и Вульф разработали метод декомпозиции для решения задач высокой размерности со специальной структурой матрицы ограничений [31].

Этот метод оказался наиболее эффективным для решения задач, матрица ограничений которых имеет блочно-диагональный вид с небольшим числом переменных. Однако, как показали дальнейшие исследования, метод применим также и для задач ЛП с матрицей общего вида. Соответствующий метод предложен Д.Б.Юдиным и Э.Г.Гольштейном и называется “блочным программированием” [12].

Отличительной особенностью метода декомпозиции является использование координинующей задачи, которая имеет по сравнению с исходной небольшое число строк и большое число столбцов. Существенным является то, что для решения координирующей задачи не требуется задания всех столбцов в явном виде. Они генерируются в процессе использования симплекс-метода. Такой подход называют методом генерации столбцов.

25) Вращательно движение вокруг неподвижной оси- Это период вращения

Количество вращений за единицу времени.

26)___ Поворот тела на некоторый угол "фи" можно задать в виде отрезка, длинна которого равна "фи", а направление совпадает с осью вокруг которой происходит поворот. Направление вектора связано с направлением вращения правила правого винта. _  Если представить, что мы взяли тело в правую руку и вращаем его в направлении, куда указывают четыре пальца, то оттопыренный большой палец покажет в ту сторону, куда направлена угловая скорость при таком вращении. __________

27) Таким образом, угловая скорость тела в данный момент времени равна первой производной от угла поворота по времени. Угловая скорость измеряется в    и может быть как положительной, так и отрицательной. Угловая скорость    по­ложительна, если в данный момент вращение происходит против движения ча­совой стрелки, и отрицательна - в противоположном случае.

Зная зависи­мость угловой скорости    от времени  , можно определить ее среднее прира­щение за единицу времени

28, 29.

Угол поворота - это физическая величина, характеризующая поворот тела, или поворот луча, исходящего из центра вращения тела, относительно другого луча, считающегося неподвижным.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Линейная скорость точки

Если (  = const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2. Так как промежутку времени t = T соответствует   = 2, то   = 2/T, откуда

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

откуда

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор   сонаправлен вектору   (рис.8), при замедлен­ном — противонаправлен ему 

30) Первый закон Ньютона гласит, что тело движется прямолинейно и равномерно, или находится в состоянии покоя, если результирующая всех действующих на тело сил равна нулю.

31) Инерциальной называется система отсчета, по отношению к которой пространство является однородным и изотропным, а время - однородным.  В такой системе отсчета свободное тело, покоящееся в некоторый момент времени, остается в покое неограниченно долго.  Кроме того, в инерциальной системе отсчета всякое свободное движение происходит с постоянной по величине и направлению скоростью (закон инерции).

32) Тела попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей центры масс этих тел (абсолютно-твердые тела), равными по модулю и противоположными по направлению:  (тоесть сила действия равна силе противодействия)

33) Размер физической величины — значения чисел, фигурирующих в значении физической величины.

34) 34. Что называют силой? Какова ее размерность? Силой называют произведение массы на ускорение: F = ma. Сила измеряется в ньютонах.

Сила характеризуется величиной и направлением.

Сила характеризует действие на данное тело других тел.

1 ньютон- это такая сила, которая действует на тело массой 1 кг, так что тело движется с ускорением 1* м/с^2

35) равнодействующая сила F₀ - сила, заменяющая собой действие всех остальных сил, приложенных к телу. Вместо множества сил, тянущих тело в разные стороны, удобно использовать одну силу - равнодействующую. Равнодействующую силу находят сложением векторов всех сил, приложенных к телу. Иногда сложение векторов сил удобно заменить сложением их проекций на координатные оси.

36) вероятно здесь стоит заменить тяготеющую массу на гравитационную массу

Физическая величина с размерностью массы, входящая во второй закон Ньютона (a = F/m) и являющаяся мерой инерции тела. То есть она показывает, насколько неохотно тело меняет состояние своего движения под действием внешней силы.

Есть ещё гравитационная масса (входящая в закон всемирного тяготения). И их эквивалентность проистекает из Общей теории относительности Эйнштейна.

37) Импульсом материальной точки называется величина, равная произведению массы тела на его скорость.

Еди ница импульса силы имеет наименование ньютон-секунда. Импульс материальной точки - это вектор, равный, в механике Ньютона, произведению массы точки на ее скорость.

38) Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени. размерность импульса силы - кг*м/с

39) По́ле  — физический объект, классически описываемый математическим скалярным, векторным, тензорным, спинорным полем (или некоторой совокупностью таких математических полей), подчиняющимся динамическим уравнениям (уравнениям движения, называемым в этом случае уравнениями поля или полевыми уравнениями — обычно это дифференциальные уравнения в частных производных). Другими словами, физическое поле представляется некоторой динамической физической величиной^[1] (называемой полевой переменной^[2]), определенной во всех^[3]точках пространства (и принимающей вообще говоря разные значения в разных точках пространства, к тому же меняющейся со временем

40) тяготения — сила взаимного притяжения, действующая между всеми материальными телами

41) В физике вес измеряют именно в ньютонах, как и всякую силу. Но вот на практике (скажем, в магазине) интересует на самом деле не вес, а МАССА. А она измеряется в килограммах. И хотя для определения массы используется ВЗВЕШИВАНИЕ (то есть реально определение ВЕСА тела - для чего используется прибор, регистрирующий именно вес, силу), ответ неявно пересчитывается в массу, через ускорение сободного падения (оно постоянно, и поэтому влияет только на масштаб шкалы прибора).

42) Связи и их реакции

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными. Тела, ограничивающие свободу перемещения других тел, называются по отношению к ним связями.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

43) Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации 

44) Кинетической энергией материальной точки называется скалярная величина, которая равняется половине произведения массы точки на квадрат ее скорости.

Кинетическая энергия: характеризует и поступательное и вращательное движения;

не зависит от направления движения точек системы и не характеризует изменение этих направлений;

характеризует действие и внутренних и внешних сил. размерность кг*м/с^2

45) Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени^[1].

Различают среднюю мощность за промежуток времени 

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

46)

47)

48)

49) В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу

48. В физике консервативные силы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует следующее определение: консервативные силы — такие силы, работа по любой замкнутой траектории которых равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Примером потенциальных сил являются упругие силы, сила тяжести.

49. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу. Механическая энергия включает в себя потенциальную и кинетическую энергию.

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ

Тело или система тел может совершать работу вследствие изменения взаимного положения тел. Работу при этом совершают силы, действующие между телами или частями тела.

Примеры

1. При движении груза вниз работу совершает сила притяжения груза к Земле.

2. При распрямлении пружины работу совершает сила упругости, обусловленная взаимодействием между атомами или молекулами вещества, из которого сделана пружина

Часть механической энергии, которая определяется взаимодействием тел, называют потенциальной энергией.

Если вследствие изменения взаимного положения тел система тел совершает работу А, то согласно общей формуле, связывающей изменение энергии с совершенной работой, изменение потенциальной энергии ΔE_п = -А.

При подъеме груза массой m на высоту h над поверхностью Земли сила тяжести совершает отрицательную работу, равную -mgh, поэтому потенциальная энергия увеличивается на mgh. Удобно считать потенциальную энергию этой системы равной нулю, когда груз находится на поверхности Земли: тогда потенциальную энергию можно записать в виде Е_п = mgh.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ

Часть механической энергии, которая определяется движением тела, называют кинетической энергией.

Если вследствие изменения своей скорости тело совершило работу А, то согласно общей формуле, связывающей изменение энергии с совершенной работой, изменение кинетической энергии ΔE_к = -А.

Докажем, что

кинетическая энергия тела Е_к = mV²/2, где m — масса тела, V— его скорость.

Кинетическая энергия Е_к тела массой m, движущегося со ско­ростью v, равна работе А, совершаемой при разгоне первоначаль­но покоившегося тела до этой скорости.

Если к телу приложена постоянная сила и тело прошло путь s, то работа силы А=Fs. Согласно второму закону Ньютона F = mа, где а — ускорение тела. При движении без начальной скорости s =at²/2, V = at, откуда следует, что s = V²/at. Поэтому Е_к = A = Fs = ma(V²/2a) = mV²/2.