Вопрос 12 Напишите формулу Ньютона-Лейбница и объясните смысл всех ее величин.
Пусть
функция y
= f(x) непрерывна
на отрезке [a;
b] и F(x) -
одна из первообразных функции на этом
отрезке, тогда справедлива формула
Ньютона-Лейбница: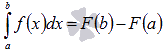 
.
Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.
Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.
Если
функция y
= f(x) непрерывна
на отрезке [a;
b],
то для аргумента 
интеграл
вида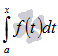 
является
функцией верхнего предела. Обозначим
эту функцию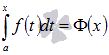 
,
причем эта функция непрерывная и
справедливо равенство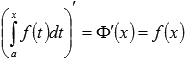 
.
Действительно,
запишем приращение функции 
,
соответствующее приращению аргумента 
и
воспользуемся пятым свойством
определенного интеграла и
следствием из десятого свойства:
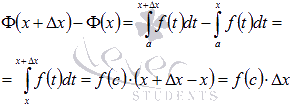где 
.
Перепишем
это равенство в виде 
.
Если вспомнить определение
производной функции и
перейти к пределу при 
,
то получим 
.
То есть,
-
это одна из первообразных функции y
= f(x) на
отрезке [a;
b].
Таким образом, множество всех
первообразных F(x) можно
записать как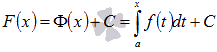 
,
где С –
произвольная постоянная.
Вычислим F(a),
используя первое свойство определенного
интеграла: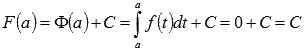 
,
следовательно, 
.
Воспользуемся этим результатом при
вычислении F(b):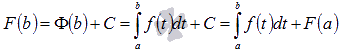 
,
то есть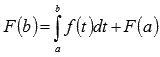 
.
Это равенство дает доказываемую формулу
Ньютона-Лейбница
.
Приращение
функции принято обозначать как 
.
Пользуясь этим обозначением, формула
Ньютона-Лейбница примет вид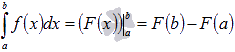 
.
Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразныхy=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке. В статье методы интегрирования разобраны основные способы нахождения первообразной. Приведем несколько примеров вычисления определенных интегралов по формуле Ньютона-Лейбница для разъяснения.
Вопрос 13 Каков геометрический смысл определенного интеграла? Вычисление площади фигуры является одной из наиболее не простых проблем теории площадей. В школьном курсе геометрии мы научились находить площади основных геометрических фигур, например, круга, треугольника, ромба и т.п. Однако намного чаще приходится сталкиваться с вычислением площадей более сложных фигур. При решении подобных задач приходится прибегать к интегральному исчислению.
В этой статье мы рассмотрим задачу о вычислении площади криволинейной трапеции, причем подойдем к ней в геометрическом смысле. Это позволит нам выяснить прямую связь между определенным интегралом и площадью криволинейной трапеции.
Пусть функция y = f(x) непрерывна на отрезке [a; b] и не меняет знак на нем (то есть, неотрицательная или неположительная). Фигуру G, ограниченную линиями y = f(x), y = 0, x = a и x = b, называют криволинейной трапецией. Обозначим ее площадь S(G).
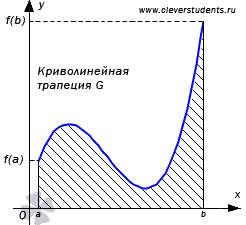
Подойдем
к задаче вычисления площади криволинейной
трапеции следующим образом. В
разделе квадрируемые
фигуры мы
выяснили, что криволинейная трапеция
является квадрируемой фигурой. Если
разбить отрезок [a;
b] на n частей 
точками 
и
обозначить 
,
а точки 
выбирать
так, чтобы 
при 
,
то фигуры, соответствующие нижней и
верхней суммам Дарбу, можно считать
входящей P и
объемлющей Q многоугольными
фигурами для G.
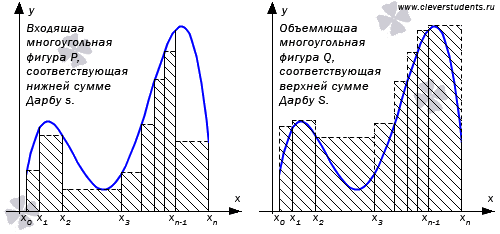
Таким
образом, 
и
при увеличении количества точек
разбиения n,
мы придем к неравенству 
,
где 
-
сколь угодно малое положительное число,
а s и S –
нижняя и верхняя суммы Дарбу для данного
разбиения отрезка [a;
b].
В другой записи 
.
Следовательно, обратившись к понятию
определенного интеграла Дарбу,
получаем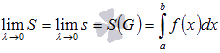 
.
Последнее
равенство означает, что определенный
интеграл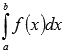 
для
непрерывной и неотрицательной функции y
= f(x) представляет
собой в геометрическом смысле площадь
соответствующей криволинейной трапеции.
В этом и состоит геометрический
смысл определенного интеграла.
То есть, вычислив определенный интеграл , мы найдем площадь фигуры, ограниченной линиями y = f(x), y = 0, x = a и x = b.
Замечание.
Если
функция y
= f(x) неположительная
на отрезке [a;
b],
то площадь криволинейной трапеции может
быть найдена как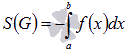 
.
Пример.
Вычислить
площадь фигуры, ограниченной линиями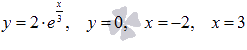 
.
Решение.
Построим
фигуру на плоскости: прямая y
= 0 совпадает
с осью абсцисс, прямые x
= -2и x
= 3 параллельны
оси ординат, а кривая 
может
быть построена с помощьюгеометрических
преобразований графика функции 
.
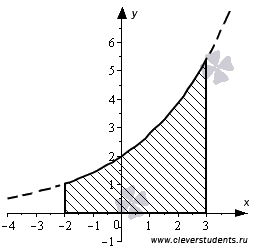
Таким
образом, нам требуется найти площадь
криволинейной трапеции. Геометрический
смысл определенного интеграла нам
указывает на то, что искомая площадь
выражается определенным интегралом.
Следовательно,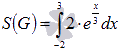 
.
Этот определенный интеграл можно
вычислить по формуле
Ньютона-Лейбница:
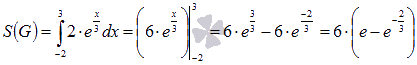
Замечание.
При
нахождении площадей криволинейных
трапеций совсем не обязательно сначала
строить эту фигуру. Если Вы знаете, что
функция y
= f(x) неотрицательная
на отрезке [a;
b] (как
в нашем примере) или неположительная,
то можно сразу применять формулы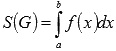 
.