Вопрос 11 Что называют определенным интегралом функции? Приведите примеры. Определенный интеграл Римана.

Рассмотрим функцию y = f(x), которая определена на отрезке [a; b]. Разобьем отрезок [a; b] наn частей   точками  .

Обозначим  , а точки   будем выбирать так, чтобы  при  . Внутри каждого отрезка   выберем точку  .

При озвученных условиях существует множество способов выбора точек   и .

Интегральной суммой функции y = f(x) для данного разбиения отрезка [a; b] и данного выбора точек   называют выражение

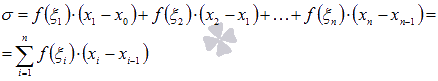
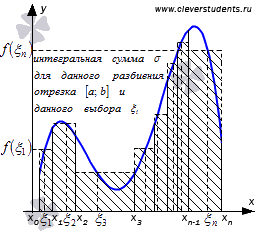
Для конкретного разбиения отрезка [a; b] и выбора точек   мы получим свою интегральную сумму. То есть, мы имеем множество интегральных сумм для различных вариантов выбора   и  .

Число   называется пределом интегральных сумм   при  , если для любого сколь угодно малого положительного ипсилон   существует такое сколь угодно малое положительное, зависящее от ипсилон, дельта  , что как только  , то при любом выборе точек   справедливо неравенство  .

Функция y = f(x) называется интегрируемой на отрезке [a; b], если существует конечный предел ее интегральных сумм при  . Значение предела есть определенный интеграл Римана.

Принято следующее обозначение интеграла Римана: 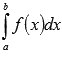 . Тогда по определению определенного интеграла Римана имеем  .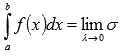

Числа a и b называются нижним и верхним пределом интегрирования соответственно, f(x)называется подынтегральной функцией, x – переменной интегрирования.

Значение определенного интеграла Римана не зависит от переменной интегрирования, то есть, .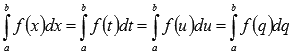

Определенный интеграл Дарбу.

Для понимания необходимого и достаточного условия существования определенного интеграла Дарбу нам потребуется несколько дополнительных определений.

Рассмотрим ограниченную на отрезке [a; b] функцию y = f(x). Вновь разобьем отрезок [a; b]на n частей точками   при прежнем условии   при  . Пусть   и   - точная нижняя и точная верхняя грань множества значений функцииy = f(x) на i-ом отрезке,  . Для непрерывной и ограниченной функции  .

Выражения вида 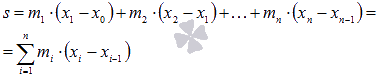и 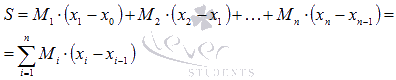   для данного разбиения отрезка [a; b] называют нижней и верхней суммами Дарбусоответственно.

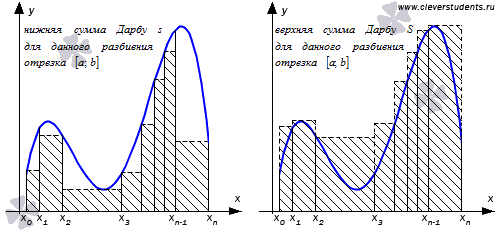
Очевидно, что для фиксированного разбиения отрезка [a; b] справедливо двойное неравенство  . Другими словами, s и S – точная нижняя и точная верхняя грань множества интегральных сумм соответственно.

Для интегрируемости ограниченной на отрезке [a; b] функции y = f(x) необходимо и достаточно, чтобы предел разности верхней и нижней сумм Дарбу был равен нулю при  , то есть, чтобы выполнялось условие  . Это условие есть необходимое и достаточное условие существования определенного интеграла Дарбу, а определенный интеграл, рассмотренный в смысле озвученного условия, называют определенным интегралом Дарбу.

Определенный интеграл Дарбу обозначают также, как и интеграл Римана, то есть,  .

Определенный интеграл Ньютона-Лейбница.

Сейчас покажем, как дается понятие определенного интеграла Ньютона-Лейбница.

Пусть функция y=f(x) имеет первообразную F(x) на отрезке [a; b], причем значение первообразной в точке x=a равно нулю: F(a)=0. Определенным интегралом Ньютона-Лейбница называется значение этой первообразной в точке b, то есть, 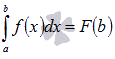  приF(a)=0.

Это определение тесно связано с формулой Ньютона-Лейбница 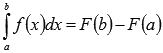 . В формуле Ньютона-Лейбница F(x) – любая первообразная из их множества, а в понятии определенного интеграла Ньютона-Лейбница фигурирует именно та первообразная, которая обращается в ноль при x=a.

Определенный интеграл Римана задается через предел интегральных сумм, интеграл Дарбу – через предел разности верхних и нижних сумм Дарбу, а интеграл Ньютона-Лейбница – через значение первообразной.

Следует отметить, что если интеграл Римана и интеграл Ньютона-Лейбница одновременно существуют для функции y = f(x) на отрезке [a; b], то их значения равны. Определенный интеграл Римана и интеграл Дарбу для ограниченной функции одновременно существуют или не существуют.