Введение

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

• даёт представления множества чисел (целых и/или вещественных);

• даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);

• отражает алгебраическую и арифметическую структуру чисел.

Системы счисления подразделяются на: позицонные, смешанные и несмешанные.Наиболее употребляемыми в настоящее время позиционными системами являются:

• 2 — двоичная (в дискретной математике, информатике, программировании);

• 3 — троичная;

• 8 — восьмеричная;

• 10 — десятичная (используется повсеместно);

• 12 — двенадцатеричная (счёт дюжинами);

• 13 — тринадцатеричная;

• 16 — шестнадцатеричная (используется в программировании, информатике);

• 60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).

В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.

Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические функции. Поскольку техника генерирования гармонических сигналов относительно проста. Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят что осуществлено спектральное разложение этого сигнала.

Задание №1

Провести следующие операции с числом, образованным номером зачетной книжки:

а) перевести в двоичную систему;

б) перевести в восьмеричную систему;

в) перевести в шестнадцатеричную систему;

г) перевести в десятичную систему числа, полученные в двоичной системе, в восьмеричной системе, в шестнадцатеричной системе, то есть сделать обратное преобразование.

Исходные данные

Номер зачетной книжки – 113217₁₀

Задание №2

а) записать математическую модель (формулу), соответствующую импульсу согласно варианту;

б) определить спектральную плотность импульса, заданного в таблице, согласно варианту;

в) построить АЧХ и ФЧХ спектральной плотности при заданной длительности импульса, амплитуде и других параметрах;

г) используя полученные графики, построить аналогичные зависимости для импульса вдвое меньше длительности. Отобразить на графиках влияние задержки импульса на время τ/2;

д) дискретизовать заданный сигнал с шагом Т;

е) записать математическую модель (формулу) дискретизованного сигнала;

ж) найти спектральную плотность дискретизованного сигнала;

з) построить амплитудный спектр дискретизованного сигнала;

Задача №1

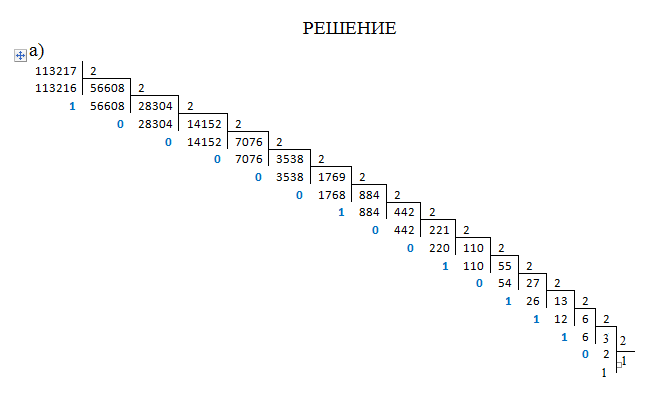
113217₁₀=11011101001000001₂

б)

113217	8
113216	14152	8
1	14152	1769	8
	0	1768	221	8
		1	216	27	8
			5	24	3
				3

113217₁₀=335101₈

в)

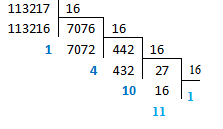
113217₁₀=1ВА41₁₆

г) 1)11011101001000001₂=2¹⁶ ·1+2¹⁵ ·1+2¹³ ·1+2¹² ·1+2¹¹ ·1+2⁹ ·1+2⁶ ·1+2⁰ ·1=

=65536+32768+8192+4096+2048+512+64+1=113217₁₀

2) 335101₈=8⁵·3+8⁴·3+8³·5+8²·1+8¹·0+8⁰·1= 98304+12288+2560+64+1=113217₁₀

3)1ВА41₁₆=16⁴·1+16³·11+16²·10+16¹·4+16⁰·1=65536+45056+2560+64+1= =113217₁₀