3.3.2. Планы второго порядка.

 Для построения полинома второй степени, имеющего вид: , в случае двух факторов, например, к точкам, образующим ядро плана и необходимым для построения линейной модели, добавляются еще точки, лежащие на осях координат ("звездные" точки), и точки в центре плана.

Общее количество точек N=n_c+n_+n₀ (n_c – количество точек, формирующих ядро плана, n_ – количество "звездных" точек, n₀ – количество точек в центре плана). Эти три множества точек как бы образуют три сферы. Свойства плана зависят от величины "звездного" плеча и от количества экспериментов в центре плана.

Например, Если "звездное" плечо равно 1 (ПФЭ 3²) будет получен ортогональный план, характеризующийся тем, что коэффициенты модели в этом случае определяются независимо друг от друга. В случае, когда "звездное" плечо (координата "звездной" точки) равно 1.414 и при n₀=5 получается ротатабельный план (в случае двух факторов), Этот план характеризуется тем, что дисперсия предсказания Y одинакова на одинаковых расстояниях от центра плана.

— Для построения моделей с двумя независимыми переменными удобно использовать программу Table Curve 3D. Эта программа дает возможность построить целый ряд моделей второго и третьего порядка, представляющих собой отрезки ряда Тейлора. Вот эти модели:

301. z=a+bx+cy+dx²+ey²+fxy

302. z=a+blnx+cy+d(lnx)²+ey²+fylnx

303. z=a+b/x+cy+d/x²+ey²+fy/x

304. z=a+bx+clny+dx²+e(lny)²+fxlny

305. z=a+blnx+clny+d(lnx)²+e(lny)²+flnxlny

306. z=a+b/x+clny+d/x²+e(lny)²+f(lny)/x

307. z=a+bx+c/y+dx²+e/y²+fx/y

308. z=a+blnx+c/y+d(lnx)²+e/y²+f(lnx)/y

309. z=a+b/x+c/y+d/x²+e/y²+f/(xy)

310. z=a+bx+cy+dx²+ey²+fxy+gx³+hy³+ixy²+jx²y

311. z=a+blnx+cy+d(lnx)²+ey²+fylnx+g(lnx)³+hy³+iy²lnx+jy(lnx)²

312. z=a+b/x+cy+d/x²+ey²+fy/x+g/x³+hy³+iy²/x+jy/x²

313. z=a+bx+clny+dx²+e(lny)²+fxlny+gx³+h(lny)³+ix(lny)²+jx²lny

314. z=a+blnx+clny+d(lnx)²+e(lny)²+flnxlny+g(lnx)³+h(lny)³+ilnx(lny)²+j(lnx)²lny

315. z=a+b/x+clny+d/x²+e(lny)²+f(lny)/x+g/x³+h(lny)³+i(lny)²/x+j(lny)/x²

316. z=a+bx+c/y+dx²+e/y²+fx/y+gx³+h/y³+ix/y²+jx²/y

317. z=a+blnx+c/y+d(lnx)²+e/y²+f(lnx)/y+g(lnx)³+h/y³+i(lnx)/y²+j(lnx)²/y

318. z=a+b/x+c/y+d/x²+e/y²+f/(xy)+g/x³+h/y³+i/(xy²)+j/(x²y)

— Программа позволяет сформировать различные варианты оформления пространственного изображения получаемой поверхности Z=f(X,Y), обеспечить качественное изображением с использованием специальных символов, подстрочных и надстрочных индексов и пр., показать на графике доверительные интервалы для отклика, дать отдельный график невязок в каждой точке плана, представляет листинг всех полученных моделей, дает результаты вычисления параметров, характеризующих качество модели (значимость коэффициентов, коэффициент детерминации, стандартная ошибка, критерий Фишера), выдает данные сравнения экспериментальных и рассчитанных значений отклика и доверительные интервалы, позволяет графически представить изменение производной отклика по каждому из факторов, позволяет рассмотреть поверхность в режиме анимации и многое другое.

Пример пространственного изображения представлен графически. Здесь же показаны линии равного уровня. К сожалению, программа не позволяеи определить , какому уровню отклика соответствует та или иная линия. Поэтому ц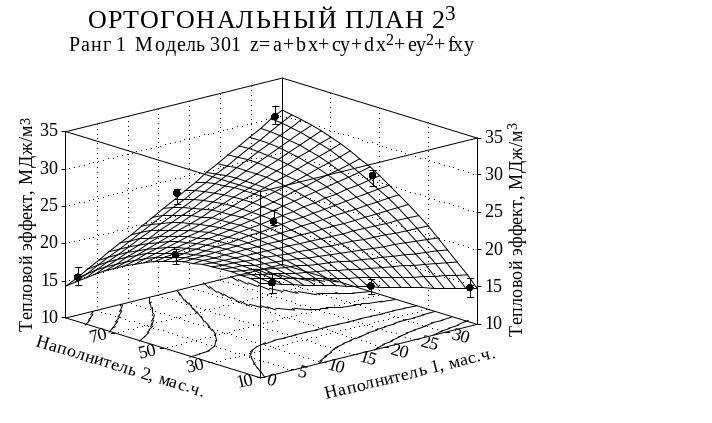 елесообразно получить уравнение в программе Table Curve 3D, а затем построить семейство изолиний в программе MatLab/