Часина третя

3.1. f(x) =x^3-3x²- ; f’(x)=3x²-6x. f’(x) = 0? Коли 3х(х-2)=0; х₁₌0; х₂=2. Зміну знаків похідної подано на рисунку.

Отже, х = 0 – точка максимуму, х = 2 – точка мінімуму.

Відповідь. х =0 – точка максимуму, х 2 точка мінімуму.

3.2. Заміна log_x y= t? тоді log_y x = . Маємо з першого рівняння: t+ t=1.

Тоді Відповідь.(6;6)

3.3. Нехай _ABCDA₁B₁C₁D_{1 –} призма, що задана в умові. Позначимо АВ=ВС= х (см), тоді, за умовою, АА₁ =2х (см). Площа бічної поверхні S_біч =Р_ABCD ·АА₁= 4х·2х= 8х² (см²). Точка К – середина ребра АА₁. Проведемо переріз через точку К і сторону DC. Цей переріз перетинає ВВ₁ у точці L. За властивістю паралельних площин, KL ║CD. Оскільки АD ┴ DC, то, за теоремою про три перпендикуляри, KD ┴ DC. Аналогічно, LC ┴ DC. Оскільки KL ║ CD, то KD ┴ KL i LC ┴ KL, отже KLCD –прямокутник. Діаметри кола, описаного навколо прямокутника, дорівнює його діагоналі, тому КС = 2·2 = 4 (см).

У

У

Тоді S_біч=8·4²=128 (см²).

Відповідь. 128 см²

Варіант 20

А

Б

В

Г

А

Б

В

Г

А

Б

В

Г

1.1

Х

1.1

Х

1.1

Х

1.2

Х

1.2

Х

1.2

Х

1.3

Х

1.3

Х

1.3

Х

1.4

Х

1.4

Х

1.4

Х

1. -10 : (-1 + 3) = -10 : 2 = -5. Відповідь. А.

1.3. Відповідь. Б.

1.6. Відповідь. Б.

1.8. Є 5 непарних цифр. З 5 цифр можна утворити двоцифрових чисел. Відповідь. А.

1.9. Відповідь. Б.

1.10. Отже, менша основа дорівнює

Відповідь. В.

1.11. Відповідь. Г.

1.12. Відповідь. А.

Частина друга

2.1. ; ;

;

1) ,

2) Розв’язків немає, бо

Відповідь. 2

2.2.

Відповідь. .

.3.

Відповідь. 0,5.

2.4. За означенням модуля вектора:

Відповідь. m = 2 або 8.

Частина третя

3.1.

Відповідь. (-∞;1]ﮞ[2;+∞).

3.2.

Знайдемо абциси точок перетину графіків:

Зобразимо схематично графіки на рисунку.

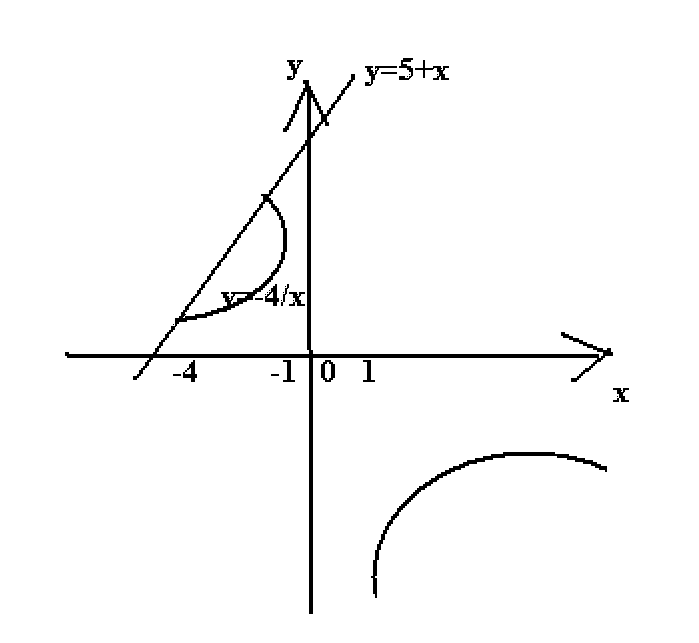
Шукана площа

S=

3.3. Нехай ABCDA_1, В_1,С_1,D₁ – призма про яку йде мова у задачі;

ABCD – ромб; BD<AC. S _{BB D D}= 36 м², S _{aa , c c} = 48 м².

Проекцією діагоналі на площину основи є BD. Тому - кут, що утворює менша діагональ призми із площиною основи. За умовою,

Позначемо BD = x. Y x tg 45 = x.

, за умовою, Тому BD= = 6 (м).

Тоді

У ;

(м)

Площа бічної поверхні

Площа повної поверхні

Відповідь.168 ( )