Частина друга

2.1. ; ;

; ;

Відповідь:

2.2. ; ; ; ;

Відповідь:

2.3. f´ f´ ; f´

Рівняння дотичної: f´ ;

Відповідь:

2.4.Нехай

, , , ,

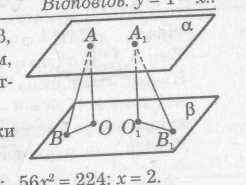
Оскільки і прямокутні . То за теоремою Піфагора: ;

Оскільки AO = A₁O₁ то:

; = ; ;

Тому AO = = Відповідь: 24см

Частина третя

3.1. Знайдемо абсциси точок перетину графіків:

; ; ; x

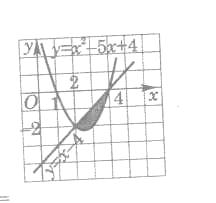
Зобразимо схематично графіки на рисунку.

Шукана площа =

Відповідь:

3.2. . Зміна тоді Маємо

Ця нерівність рівносильна системі

Тоді маємо: Нерівність виконується для всіх значень х. З отримамо . Отже, остаточно маємо: .

Відповідь:

3.3.

Нехай ABCDA₁B₁C₁B₁ – призма що задана в умові; ABCD – ромб; AB=a. Оскільки АА₁ то - кут між площинами А₁АВ і А₁АD. За умовою, - гострий кут.

Тоді AC<BD. Проекцією діагоналі А₁С на площину основи є АС, тому кут нахилу бічної діагоналі призми до площини основи.

У за теоремою косинусів: ; ; ; .

У

Тоді об´єм призми.

Відповідь:

Варіант 16

Частина перша

А	Б	В	Г
	X
		X
			X
X

	А	Б	В	Г
1,5 1,6 1,7 1,8		X
			X
				X
	X

	А	Б	В	Г
1,9 1.10 1.11 1.12			X
		X
			X
				X

1.1 1.2 1.51.6

1.3 1.61.6

1.4

1.1. . Відповідь. Б.

1.4. Відповідь. А.

1.6. Відповідь. Б.

1.7. Відповідь. Г.

1.8. Відповідь. А.

1.9. Відповідь. В.

1.11. Відповідь. В.

1.12. Відповідь. Г.