ВАРІАНТ 10
Частина перша
|
А |
Б |
В |
Г |
1.1 |
× |
|
|
|
1.2 |
|
|
|
× |
1.3 |
|
× |
|
|
1.4 |
|
|
× |
|
|
А |
Б |
В |
Г |
1.5 |
|
|
|
× |
1.6 |
|
|
× |
|
1.7 |
× |
|
|
|
1.8 |
|
× |
|
|
|
А |
Б |
В |
Г |
1.9 |
|
|
× |
|
1.10 |
|
|
|
× |
1.11 |
× |
|
|
|
1.12 |
|
× |
|
|
( 7-5 + 6 ) · 3 = 8 · 3 = 24. Відповідь. А.
1.3
:
=
·
=
-
Відповідь.
Б.
1.8. 6 · 6 = 36. Відповідь. Б.
1.9. 360˚ : 6 = 60˚. Відповідь. В.
1.10 180˚ - (90˚+ 32˚) = 58˚. Відповідь. Г.
1.12.
;
;
;
Відповідь.
Б.
Частина друга
2.1.
;
;
;
Відповідь.
2.2. Заміна:
Маємо:
;
;
;
х є
. Відповідь.
.
2.3. Тіло зупиниться, коли швидкість його руху дорівнюватиме нулю.
Відповідь.
4,5 с.
2.4. Діагоналі АС і BD паралелограма ABCD перетинаються і точкою перетену діляться навпіл. Знайдемо цю точку О як середину BD:
=
О
Нехай
Оскільки
О – середина відрізка АС, то
Відповідь.
А( -6;20;-4).
Частина третя
3.1.
Відповідь. 6
3.2.
З другого рівняння маємо: t1= - 1; t2=3; z2 = - 1.
1)
2)
Відповідь.
(-1;27),(27;-1).
На рисунку зображено конус та переріз QAB, про
який йде мова у задачі,
за
умовою.
Нехай ОК – висота
тоді,
за теоремою про три
перпендикуляри, QK
AB,
а отже, площина QKO
перпендикулярна до АВ, тому
кут,
який
утворює площина перерізу з площиною основи. За
умовою,
-
висота конуса.
У
QK – медіана, висота і бісектриса у рівнобедреному трикутнику QAB.
Тому
У
OB = r – радіус основи конкурса.
У
Тоді об’єм конуса V
Відповідь.
ВАРІАНТ 11
Частина перша
|
А |
Б |
В |
Г |
|
|
А |
Б |
В |
Г |
|
|
А |
Б |
В |
Г |
1.1 |
|
Х |
|
|
|
1.5 |
|
Х |
|
|
|
1.9 |
|
|
Х |
|
1.2 |
|
|
|
Х |
|
1.6 |
Х |
|
|
|
|
1.10 |
|
|
|
Х |
1.3 |
|
Х |
|
|
|
1.7 |
|
|
Х |
|
|
1.11 |
Х |
|
|
|
1.4 |
|
|
Х |
|
|
1.8 |
|
|
|
Х |
|
1.12 |
|
Х |
|
|
1.1. (12 - 8) 5 = 4 * 5 = 20. Відповідь.Б
1.4. q = b2 : b1 = -0,5; b4 = b1q3 = 64 * (-0,5)3 = -8 Відповідь В.
1.6. log5 250 - log5 2 = log5 53 * 2 - log5 2 = log5 53 + log5 2 - log5 2 = 3.
Відповідь А.
1.8.
(х
+ 1)dx =
=
+
2 = 4. Відповідь Г.
1.10. Sсек. =
*
= 8
(см2). Відповідь Г.
1.11. V =
=
= 48 (см3). Відповідь А.
1.12.
~
(
спільний, АВ
).
А
Тому
=
;
=
;
АВ = 6 (см). С Відповідь Б.
А В
С
Частина друга
2.1.
= 50;
=
;
=
;
=
;
х =
. Відповідь
0,5.
2.2. Кількість усіх можливих комбінацій виймання кульок - 5! = 120.
Потрібна комбінація тільки одна. Тому
ймовірність настання вказаної події
дорівнює
. Відповідь
.
2.3.
-
=
5. ОДЗ:
› 0. Заміна:
= а › 0.
2а-
= 5;
= 0; D = 25 + 24 = 49; а1’2 =
;
а1 = -0,5, а2 = 3.
Враховуючи умови, маємо: = 3; х - 1 = 9; х = 10. Відповідь. 10.
2
.4.
АВВА1А1 -
квадрат, А1В =
см.
Точку АВ = АА1 = Н = (6
см). ОЕ
АВ,
ЕВ =АВ/2 = 3 (см). А1
У
ΔОЕВ
: ОЕ = 2ОВ (за умовою), тому
.
О
В
=
(см).
Отже, радіус основи R
=
см.
В
Sбіч. = 2
RH
= 2
(см2). Відповідь.
см2.
Частина третя
3.1.
; 0<
х2 + 4х ≥ (0,2)-1; 0<х2
+ 4х ≥ 5. Маємо систему рівнянь
ВАРІАНТ 12
Частина прерша
|
А |
Б |
В |
Г |
1.5 |
|
|
Х |
|
1.6 |
|
Х |
|
|
1.7 |
|
|
|
Х |
1.8 |
|
|
Х |
|
|
А |
Б |
В |
Г |
1.9 |
|
|
Х |
|
1.10 |
|
Х |
|
|
1.11 |
|
Х |
|
|
1.12 |
Х |
|
|
|
|
А |
Б |
В |
Г |
1.1 |
Х |
|
|
|
1.2 |
Х |
|
|
|
1.3 |
|
Х |
|
|
1.4 |
|
|
Х |
|
1.1.
Відповідь
А.
1.4.
Максимальна
кількість костюмів — 5 Відповідь В.
1.6.
Відповідь
Б.
1.7.
Відповідь
Г.
1.8.
Відповідь
В.
1.9.
Відповідь
В.
1.10.
Відповідь Б.
1.11.
Відповідь
Б.
1.12. Нехай
тоді
оскільки трикутники рівні, то
З
Відповідь А.
Частина друга
2
+
-
+
Як бачимо, при
функція
набуває мінімального значення
а
при
функція набуває максимального значення
Відповідь -1;7.
2.2. ОДЗ:
—
Не входить в ОДЗ,
Відповідь
6.
2.3. Первісна для даної функції має вигляд:
Знайдемо
Остаточно маємо:
Відповідь
2.4. У
Нехай
тоді
За
теоремою Піфагора, маємо:
.
Відповідь
Частина третя
3.1.
,
коли
Зміну знаків похідної дано на рисунку.
Отже,
— точка мінімуму,
— точка максимуму.
Відповідь. — точка мінімуму, — точка максимуму.
3
.2.
,
тоді
y
Маємо
Враховуючи, що
,
маємо
,
тоді
Маємо
Це рівняння не має розв’язків, що
задоволняють умову
Враховуючи, що
,
маємо
Відповідь.
3.3. Нехай піраміда QABCD така, що ABCD — квадрат і QDC ABC та QDA ABC. Звідси отримуємо, що QD ABC, а томубічне ребро QD є також висотою піраміди, а точка D — основої цієї висоти.
З бічних ребер піраміди найбільшими є
те, яке має найбільшу проекцію, тобто
ребро QB. За умовою.
.
Нехай DK — відстан0ь від точки D до середини ребра QB. За умовою, DK=d. Оскільки DK — мередіана прямокутного трикутника, що проведена до гіпотенузи, то QВ = 2d.
У
АBCD — квадрат, нехай DC
= BC = x, тоді
Відповідь.
ВАРІАНТ 13
Частина перша
|
А |
Б |
В |
Г |
1.5 |
|
|
Х |
|
1.6 |
|
Х |
|
|
1.7 |
Х |
|
|
|
1.8 |
|
|
|
Х |
|
А |
Б |
В |
Г |
1.9 |
|
|
|
Х |
1.10 |
|
Х |
|
|
1.11 |
Х |
|
|
|
1.12 |
|
|
Х |
|
|
А |
Б |
В |
Г |
1.1 |
|
|
Х |
|
1.2 |
Х |
|
|
|
1.3 |
|
Х |
|
|
1.4 |
|
|
|
Х |
1.4 х+3>2x-7; х<10 Відповідь Г.
1.7 F´(x) = (3-cosx)´= sinx Відповідь A.
1.8 f (x)
= 3x2-12. 3x-12
= 0; х2 = 4; х =
2
Отже, функція спадає на проміжку х
[-2;2] Відповідь Г.
1.9
Відповідь
Г.
1.10 ВС = АВ
= 9 (см) Відповідь Б.
1.11 S =
(cм2) Відповідь
А.
1.12
.
Тому
. Відповідь
В.
Частина друга
2.1 Нехай шукані числа х і у. Тобто
х < log
11
< у. Перетворимо дану нерівність,
врахувавши що
< 1.
<
<
.
Або 2-у < 11<2-х
. Дану нерівність задовольняють
числа х = -4, у = -3. Відповідь.
-4; -3.
2.2
х>0 : х(х-1) = 110; х2 –
х – 110 = 0; х
= 11, х
=
10 – не є корнем.
Відповідь. 11.
S
=
= 6
(м).
Відповідь 50 м
SABC – правильна трикутна піраміда, SO - висота, апофема бічної грані SAB; Н – середина SO; L – середина SM; HL = 2 см.
У
:
HL – середня лінія, OM
= 2 HL = 4 cм.
.
Тому SO = OM=
4 см. OM – радіус кола,
вписаного у правильний
(см).
S
=
(cм2).
V =
(cм2)
.
Відповідь
(cм2)
Частина третя
2log
(-х)>
log
(10-9
х).
ОДЗ нерівності визначимо із системи:
,
тобто х<0.
Далі маємо log
(-x)2
>log
(10-9);
х2 <10-9х; х2 +9х-10<0.
Дана нерівність виконується при -10 <х<1 (див.рисунок). Враховуючи ОДЗ, остаточно отримаємо (-10;0).
Відповідь (-10;0)
cos2х+
.
cosх
,
тоді
;
cosх
.
а) cosх = 0;
х
=
k,
;
б) cosх +
sinх
=
,
tgх =
;
х = -
,
l
Z.
Враховуючи, що cosх
,
маємо
х2 =
,
m
Z.
2) cosх < 0, тоді
;
cosх
.
а) cosх = 0. Це рівняння не має розв’язків, що задовольняють умову cosх < 0.
б) cosх
;
tgх =
;
х =
,
l
Z.
Враховуючи, що cosх <
0, маємо х3 =
,
n
Z.
Відповідь: k, k Z.
Нехай ABCDA1B1C1D1 – призма, що задана в умові; ABCD – ромб; AC > BD. У призмі проведено переріз AB1C; S
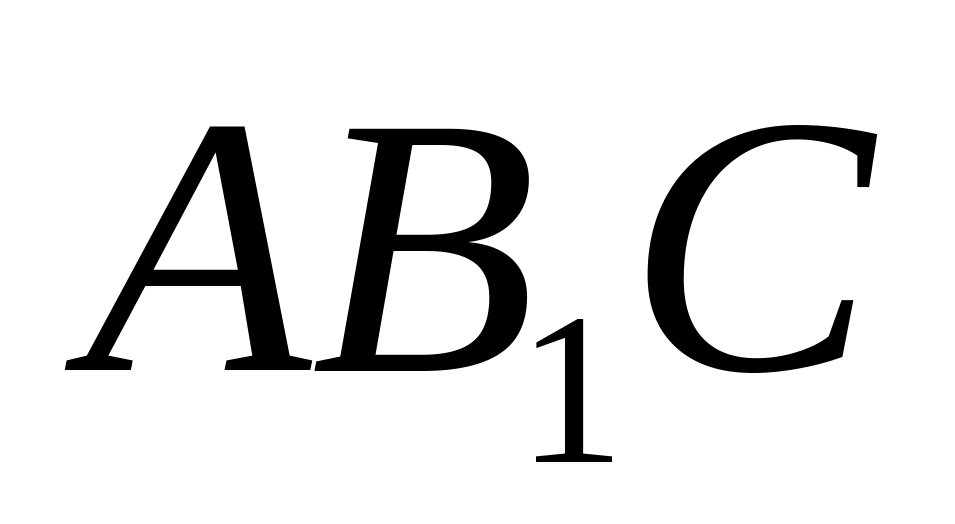= 36 см2,
AB1C
= 60
Оскільки
є ортогональною проекцією
на площину основи, то S
= S
, де
- кут між площинами перерізу та основи.
Отже, S
=
(см2).
Тоді S
(см2).
BO
AC,
тоді, за
теоремою про
три перпендикуляри,
B1O
AC,
тому BOB1
AC
і
BOB1
– кут
між площинами
перерізу і
нижньої основи.
За умовою
BOB1
=
.
(за
двома катетами), тому АВ = В1С і
-
рівнобедрений.
Оскільки
AB1C
=
,
то
,
-
рівносторонній. Позначимо
,
тоді
;
;
.
У
:
.
У
:
(см).
Тоді об’єм призми
.
Відповідь:
см3.
Варіант 14
Частина перша
|
а |
б |
в |
г |
|
|
а |
б |
в |
г |
|
|
а |
б |
в |
г |
1,1 |
|
|
|
X |
|
1,5 |
|
|
|
|
|
1,9 |
|
|
|
|
1,2 |
|
|
|
|
|
1,6 |
|
|
|
|
|
1,10 |
|
|
|
|
1,3 |
|
|
|
|
|
1,7 |
|
|
|
|
|
1,11 |
|
|
|
|
1,4 |
|
|
|
|
|
1,8 |
|
|
|
|
|
1,12 |
|
|
|
|
1.1. x км – весь шлях.
Відповідь.
Г.