Постановка задачи

Из уравнений Максвелла следует, что вектор электрического поля световой волны E(r, t) удовлетворяет волновому уравнению

(1)

где с – скорость света, Δ – оператор Лапласа, который в декартовы координатах имеет вид

В нашем случае задача обладает осевой симметрией, поэтому удобно перейти к цилиндрическим координатам ρ, φ, z. В этом случае оператор Лапласа записывается следующим образом:

и уравнение (1) принимает вид

(2)

Будем искать решение уравнения (2) в виде

где k=ω/c=2π/λ – волновое число. Так как мы рассматриваем установившееся распределение световой волны после прохождения отверстия, то амплитуда А от времени не зависит. Отметим, что амплитуда – функция комплексного переменного.

Подставляя этот вид решения в уравнение, получим уравнение для амплитуды

(3)

Будем считать, что амплитуда достаточно медленно изменяется вдоль оси z, т.е.

(4)

Тогда уравнение (3) упрощается

(5)

Полученное уравнение называют параболическое уравнение дифракции. Его мы и будем решать.

Решение параболического уравнения дифракции

Решать уравнение дифракции будем с помощью интегральных преобразований Ханкеля. Прямое преобразование Ханкеля нулевого порядка преобразует исходную функцию f(ρ) переменной ρ в функцию F(s) новой переменной s согласно выражению:

По известной функции F(s) можно восстановить вид функции f(ρ) с помощью обратного преобразования Ханкеля

здесь J₀(x) – функция Бесселя первого рода нулевого порядка. Ее график приведен на рис.2.

I₀(r)

r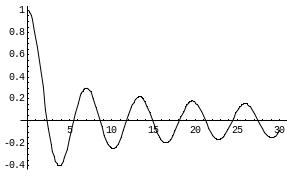

Рис.2. График функции Бесселя первого рода нулевого порядка

Преобразование Ханкеля целесообразно применять тогда, когда в уравнении встречается комбинация производных, стоящая в правой части (5), так как основное свойство этого преобразования следующее:

Применив преобразование Ханкеля по переменной ρ к уравнению (5), получим

или

(6)

Поскольку амплитуда теперь является функцией только одной переменной z (переменная s может рассматриваться просто как параметр, поскольку по ней дифференцирование не производится), то частную производную можно заменить на полную производную.

Решение уравнения (5) легко находим методом разделения переменных:

, (7)

где А(0) – значение A(s,z) при z=0.

Будем считать падающую на отверстие в экране волну плоской, т.е. распределение амплитуды по сечению отверстия однородным с постоянной фазой

Для дальнейшего рассмотрения удобно перейти к безразмерным переменным

,

Комбинация переменных πR²/λ называется длина Рэлея.

В дальнейшем знак ~ над буквой писать не будем для упрощения формы записи.

В новых переменных исходное уравнение (5) запишется как

а образ Ханкеля его решения (7)

(8)

A(s,z) при z=0 находим как

Подставляя полученное выражение в (7) получим образ решения параболического уравнения (5)

где J₁(s) – функция Бесселя первого рода первого порядка. Ее график представлен на рис.3.

I_l(r)

r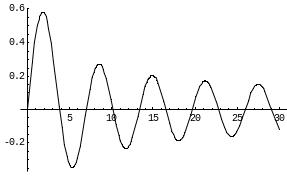

Рис.3. График функции Бесселя первого рода первого порядка

Само решение получим, взяв обратное преобразование от A(s,z)

(9)

Выражение (9) позволяет определить амплитуду, интенсивность и фазу волны после прохождения ею круглого отверстия в экране. Так, интенсивность волны пропорциональна квадрату модуля амплитуды, и ее удобно нормировать на интенсивность волны в плоскости отверстия, т.е. при z=0:

(10)

(в дальнейшем знак ~ будем опускать).

Кроме того, с помощью рассмотренной модели можно рассчитать процесс распространения ограниченных в пространстве волновых пучков, в частности, лазерных.

Отметим еще раз, что полученное решение будет справедливо при выполнении условия (4), которое в безразмерных переменных будет выглядеть следующим образом

(11)

(множитель i под знаком модуля в правой части (10) можно опустить).