ЗАДАНИЕ № 1.

Расчет центрированной оптической системы.

1.Раcсчитать параметры толстой линзы:

оптическую силу, главные фокусные расстояния, положение главных плоскостей.

Основные формулы:

1. Сферическая поверхность.

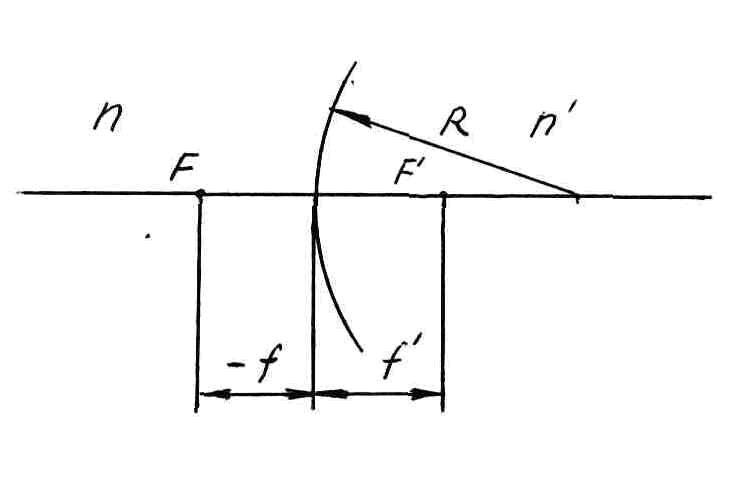
Рис.1

Оптическая сила сферической поверхности :

Главные фокусные расстояния:

; ;

2. Толстая линза.

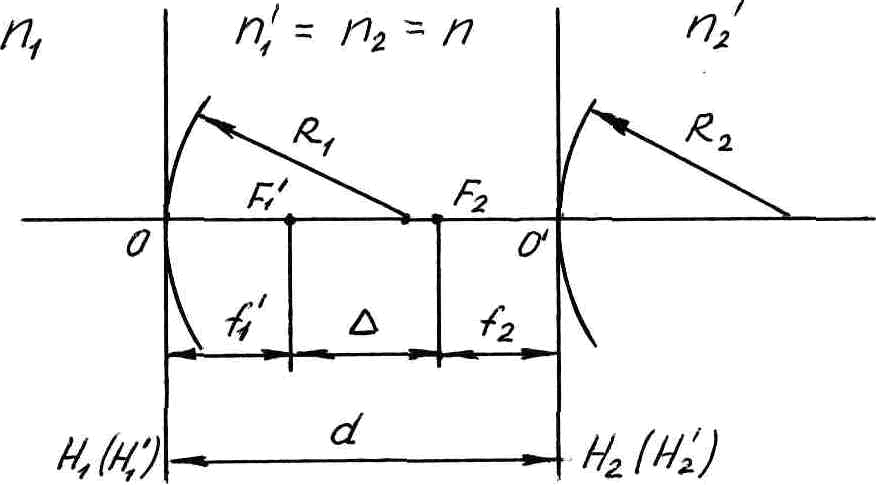
Рис.2

Оптическая сила линзы:

;

где Ф₁ и Ф₂ - оптические силы первой и второй сферических поверхностей;

d - толщина линзы;

n - показатель преломления линзы;

Положение главных плоскостей:

(отсчет от О)

(отсчет от О’)

Оптический промежуток:

где f₁ и f₂ -главные фокусные расстояния первой и второй сферических поверхностей.

Главные фокусные расстояния линзы:

; ;

Расчет произвести для двух линз.

Данные для своего варианта получить у преподавателя.

2. Рассчитать параметры центрированной оптической системы, состоящей из двух линз.

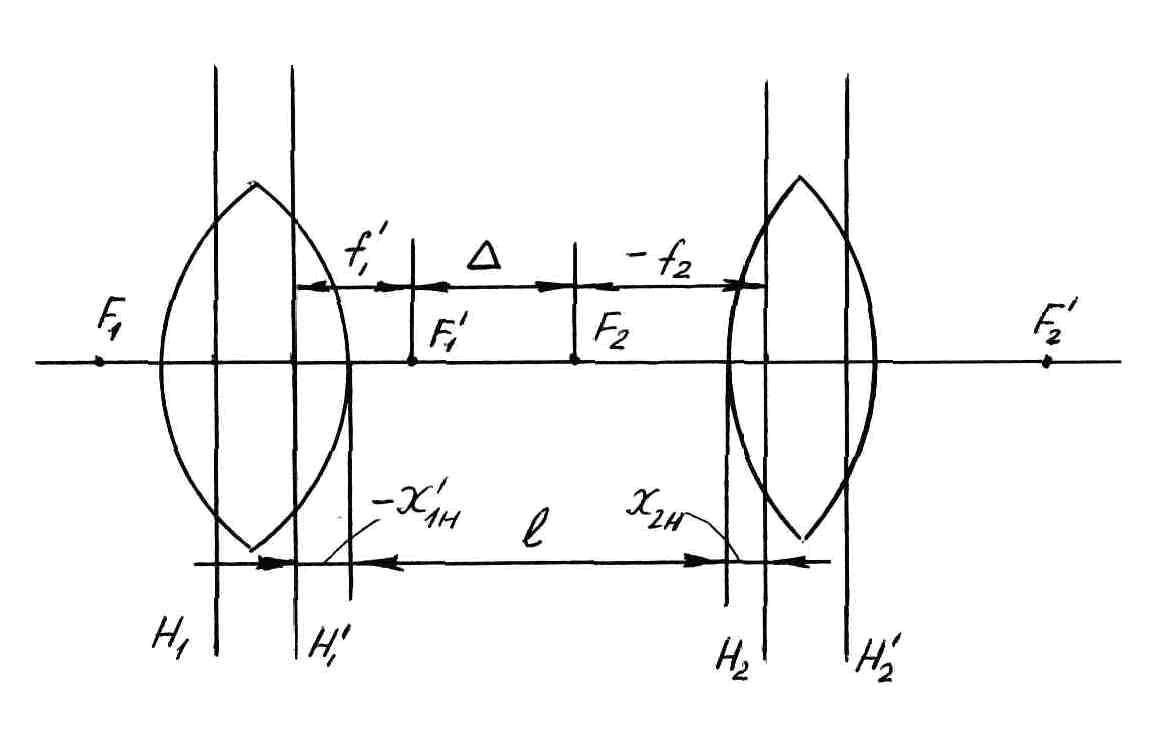
Рис. 3

Рис.4

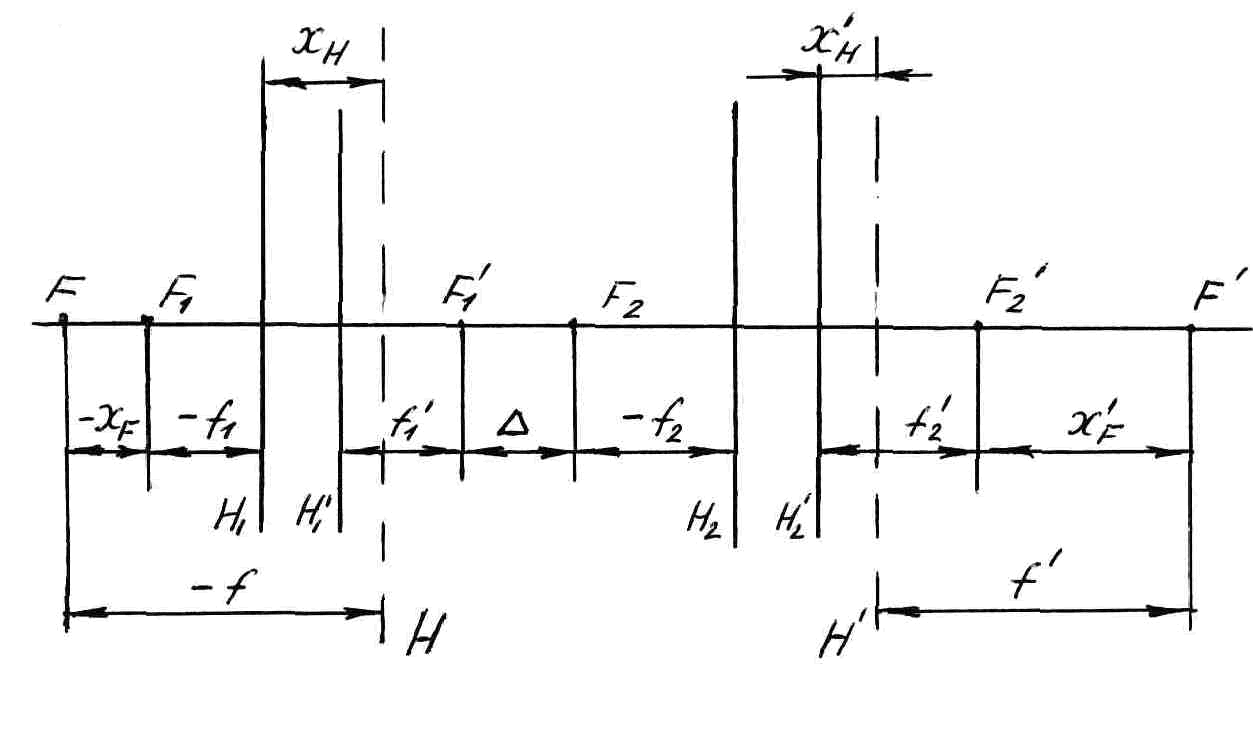
Главные фокусные расстояния системы:

; ;

где  - оптический промежуток .

Из рис.3 находим :

f₁ +  - f₂ = - X_1H + l + X_2H

откуда определить  ; величины подставлять со своими знаками.

Положение главных плоскостей системы:

Х_Н = ;

X_H = ;

X_H - отсчитывается от первой главной плоскости системы I ( от Н₁ );

Х_H – отсчитывается от второй главной плоскости системы II ( от Н₂).

Главные фокусные расстояния f и f откладываются от главных плоскостей системы Н и Н`, положение фокусов определяется по формулам:

Х_F = (расстояние F₁F )

X_F = - (расстояние F₂ F ).

Все построения изобразить на чертеже.

3. Проверить расчет с помощью матричного метода .

Описание матричного метода:

Преобразование параметров у и V = n  при переходе от одной опорной плоскости к другой

( ОП₁ ОП₂ ) в параксиальном приближении имеют вид :

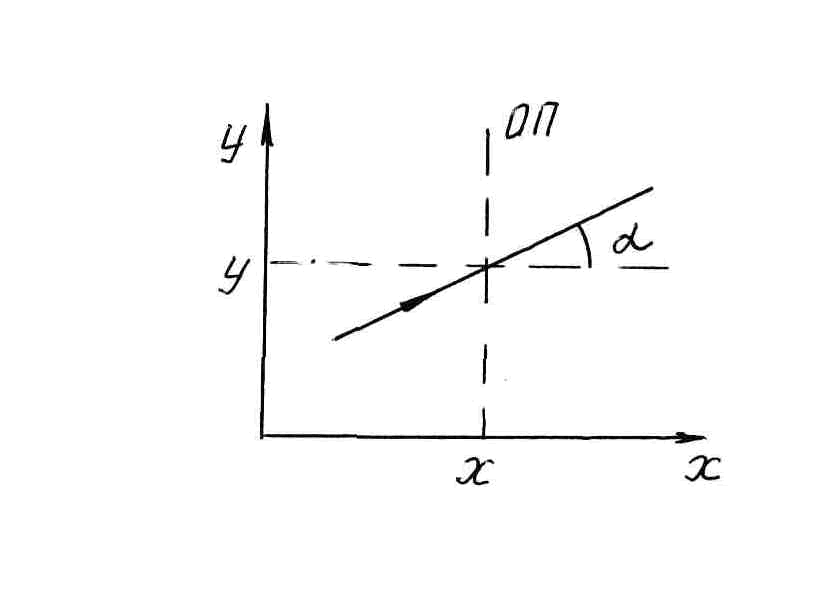
у₂ = Ау₁ + ВV₁

V₂ = Cy₁ + DV₁

или в матричном виде

Рис. 5

ОП – опорная плоскость ( х= const )

Матрица преобразования луча в сложной системе равна произведению матриц для отдельных элементов, взятых в обратном порядке.

Для исчерпывающего исследования поведения параксиального луча в центрированной оптической системе достаточно знать матрицы преобразования трех основных элементов : оптического промежутка ( т.е. участка однородной среды ), преломляющей и отражающей поверхностей.

3.1. Оптический промежуток .

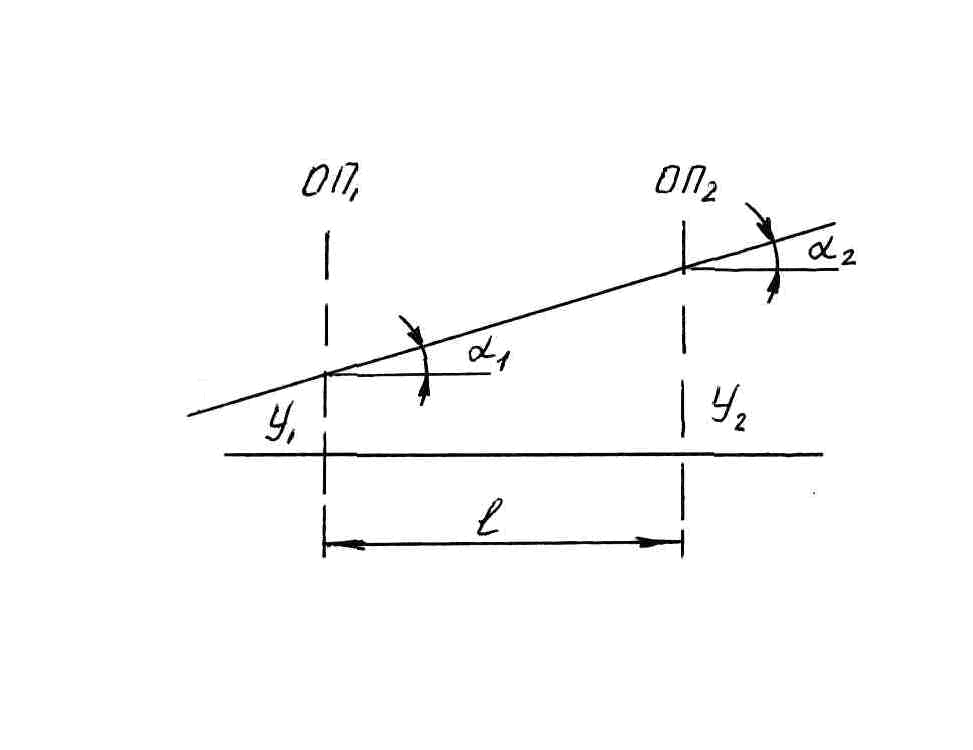
Рис.6

ОП₁ и ОП₂ – опорные плоскости.

Параметры преобразования – у и V= n .

- приведенная толщина оптического промежутка.

Формулы преобразования :

где

ℱ = - матрица оптического промежутка .

2. Сферическая поверхность .

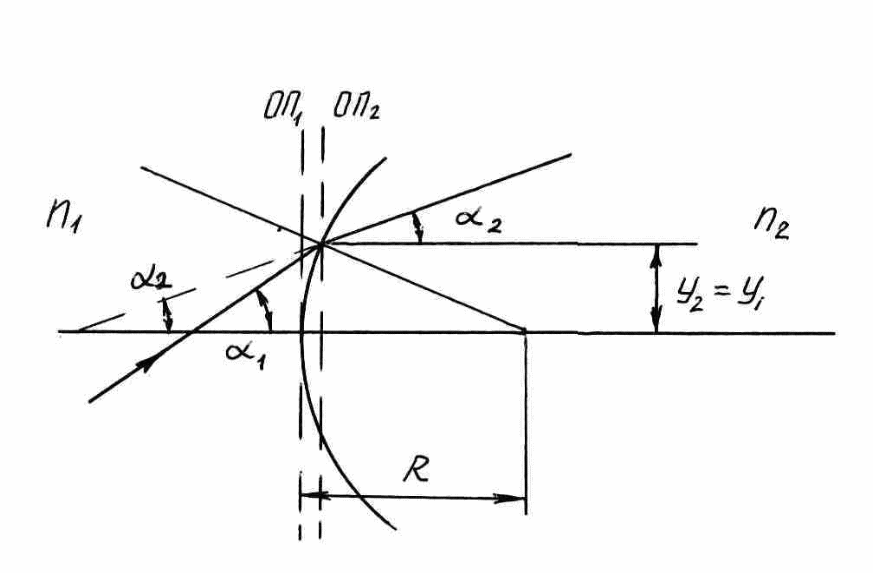
Рис. 7

Матрица преломления :

ℛ

где Ф = - оптическая сила сферической поверхности.

Формулы преобразования параметров :

2. Отражающая поверхность.

Матрица отражения :

ℛ_отр =

где Ф = - Ф < 0 R > 0 - выпуклое зеркало

Ф > 0 R < 0 - вогнутое зеркало .

Пример : Матрица преобразования для толстой линзы .

ℳ = ℛ₂ℱℛ₁

ℳ =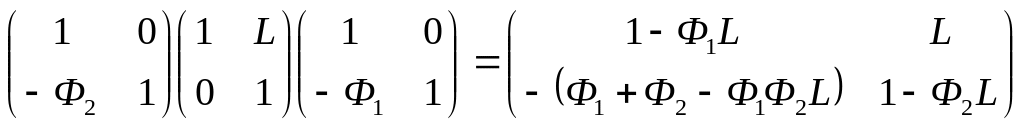

ℳ – матрица преобразования между передней (ОП₁ ) и задней ( ОП₂ ) преломляющими поверхностями оптической системы .

Этим способом можно найти полную матрицу ℳ преобразования параметров параксиального луча для произвольной центрированной оптической системы , если известны кривизна и взаимное расположение ее преломляющих и отражающих поверхностей и значения показателей преломления . Введем обозначения A , B , C и D для ее элементов :

ℳ =

При этом должно выполняется det ℳ = AD – BC=1.

В табл. 1 приведены формулы для нахождения кардинальных точек по известным элементам матрицы ℳ ( рис.8)

Табл.1.

Расстояния при n1=n2= 1
ОП1 – F	n1 D/C	D/C
H- F	f = n1/C	f= 1/C
ОП1- H	n1(D-1)/C	(D-1)/C
ОП2- F	- n2A/C	-A/C
H-F	f`= -n2/C	f =-1/C
ОП2- Н	n2 (1-A)/C	(1-A)/C

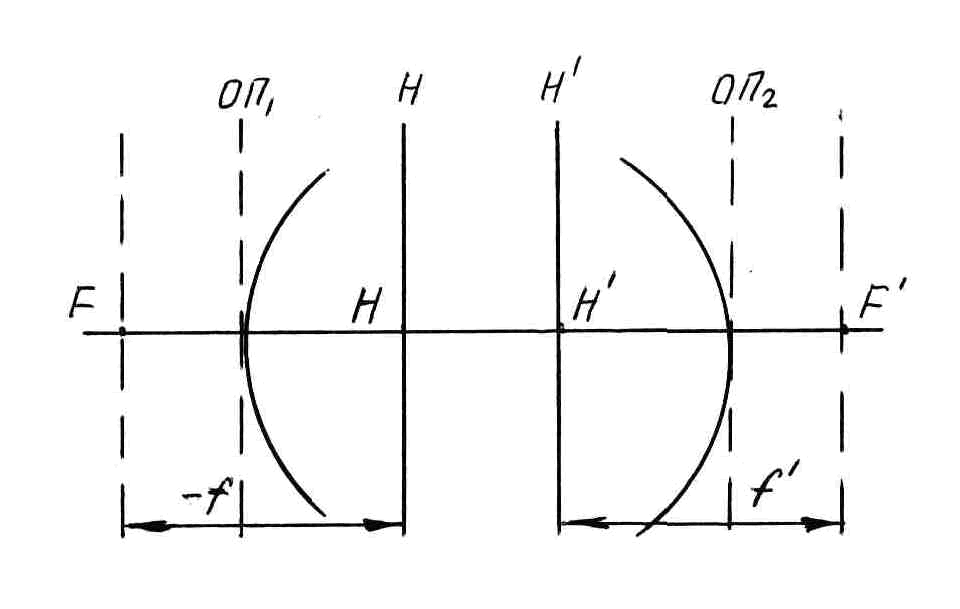
Рис. 8

Полученные значения сравнить с результатами, выполненными в п. 2.

Сделать вывод.

Пример расчета .

Задание: Линза А R₁=0.1м; R₂=-0.15 м; n₁=1; n₁ = n₂=1.5

n₂ =1 ; d= 0,03 м;

Линза Б R₁=-0.1 м; R₂= 0.1 м;

n₁=1; n₁ = n₂=1,5; n₂’=1 ; d= 0.03 м;

Расстояние между линзами l= 0.05 м.

1. Расчет линзы А :

Сферическая поверхность 1 :

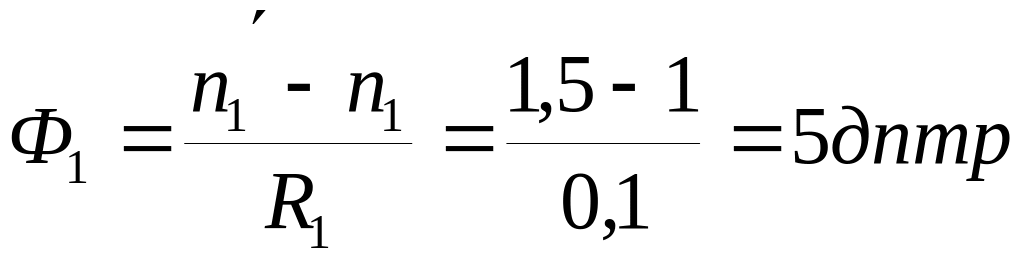
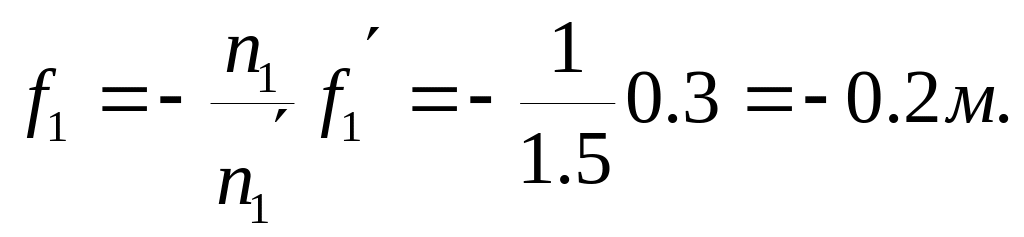
Сферическая поверхность 2:

; ;

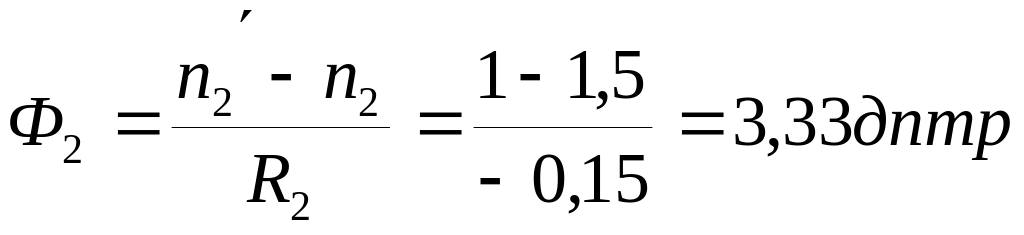
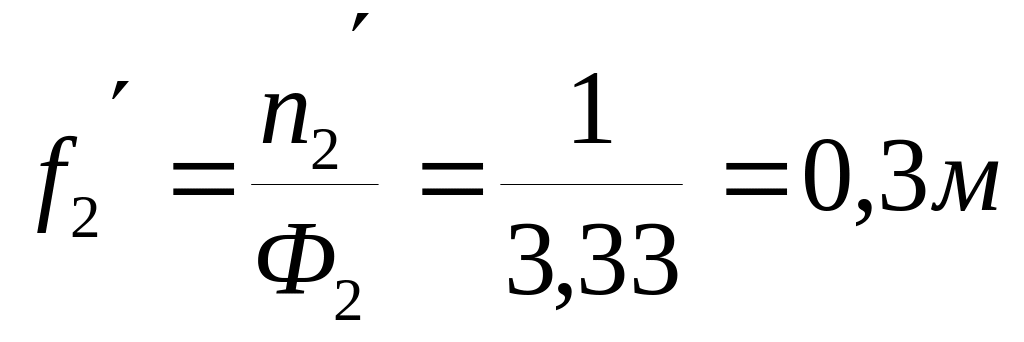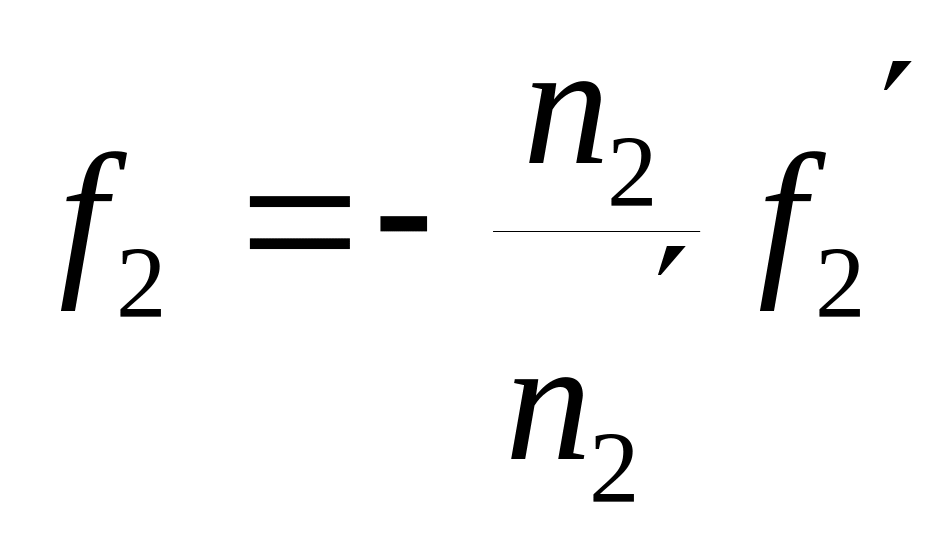
Оптическая сила линзы:

Положение главных плоскостей:

Оптический промежуток:

Главные фокусные расстояния линзы:

2. Расчет линзы Б :

Сферическая поверхность 1:

Сферическая поверхность 2:

Оптическая сила линзы:

Положение главных плоскостей:

Оптический промежуток:

Главные фокусные расстояния линзы:

3. Расчет системы :

Оптический промежуток системы:

Исходные данные для системы:

Главные фокусные расстояния системы:

Положение главных плоскостей системы:

(отсчет от Н_1А)

(отсчет от Н_Б)

(F_Б F’)

(F_A F )

4. Матричный метод:

Линза А:

ℳ

ℳ _A

ℳ _A А=0,9; В=0,02;

С=-8; D=0.9334;

Проверка: det ℳ

Расстояния:

Линза Б:

ℳ _Б

А=1,1; В=0,02; С=10,5; D=1,1;

Det ℳ = ;

Расстояния:

Расчет системы:

Матрица преобразования линзы А:

ℳ _A

Матрица преобразования оптического промежутка:

ℳ где

Матрица преобразования линзы Б:

ℳ

Для всей системы:

ℳ =ℳ _Бℳ _прℳ _А

А=0,39; В=0,092; С=-3,55; D=1,7267

Проверка:

detℳ =AD-BC=

Расстояния для системы:

Проверка:

Должно выполняться:

;

.