Замечание.

1)      Всякая точка глобального минимума является и точкой локального минимума этой функции. Обратное, вообще говоря, неверно.

2)      Аналогичные определения глобального максимума и локального максимума можно получить путем замены знака неравенства на противоположный.

3)      Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом.

4)      Если функция не является унимодальной, то возможно наличие нескольких локальных оптимумов, при этом глобальный минимум можно определить путем нахождения всех локальных оптимумов и выбора наименьшего из них.

3.6. Идентификация оптимумов

 

Теорема 1. Необходимые условия того, что х* является точкой локального минимума (максимума) дважды дифференцируемой функции f на открытом интервале (a,b), выражаются следующими соотношениями:

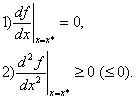
Эти условия необходимы, но не достаточны для того, чтобы точка х* была точкой локального минимума (максимума).

Определение. Стационарной точкой называется точка х*, в которой

 ,

если стационарная точка не соответствует локальному оптимуму (минимуму или максимуму), то она является точкой перегиба или седловой точкой.

Теорема 2. Пусть в точке х* первые (n-1) производные функции обращаются в нуль, а производная порядка n отлична от нуля. Тогда:

1)        если n – нечетное, то х* - точка перегиба;

2)        если n – четное, то х* - точка локального оптимума.

Кроме того,

a)    если эта производная положительная, то х* - точка локального минимума;

б)  если эта производная отрицательная, то х* - точка локального максимума.

З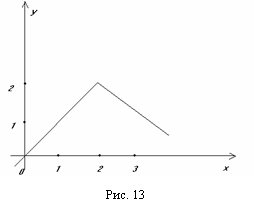 амечание. Выше предполагалось, что рассматриваемая функция дифференцируема или, что её первая производная существует и непрерывна. Однако если функция не является дифференцируемой, во всех точках области определения, то даже необходимое условие наличия оптимума, позволяющее идентифицировать стационарные точки, может не выполняться в точке оптимума.

Пример 8.

Рассмотрим функцию

 

 

Эта функция непрерывна во всех точках действительной оси, но недифференцируема при х=2. Функция достигает максимума в точке х=2, которая не является стационарной в соответствии с данным выше определением. Это подтверждает тот факт, что теорема 1 является необходимым, но не достаточным условием оптимума.

Пример 9. Найти и идентифицировать оптимумы функции

Решение. Найдем первую производную функции:

Найдем стационарные точки. Для этого решим уравнение  Следовательно,  получили единственную стационарную точку х=0. Найдем вторую производную  

Для идентификации точки оптимума, вычислим значение второй производной в стационарной точке.

х	f(x)
0	-8	2

 

Значит, х=0 – точка  минимума.

Пример 10. Найти и идентифицировать оптимумы функции

Решение. Сначала найдем первую производную функции:

.

Найдем стационарные точки. Для этого решим уравнение:

Следовательно, стационарные точки:  

Найдем вторую производную

Для идентификации точек оптимума, вычислим значение второй производной в стационарных точках.

 

x	f(x)
0	36	0
1	27.5	60
2	44	-120
3	5.5	540

 

Значит, х=1 х=3 – точки локальных минимумов, х=2 – точка локального максимума.

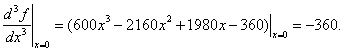
Чтобы идентифицировать точку х=0, найдем и вычислим третью производную:

Так как  и n=3 – нечетное, то (по теореме 2) х*=0 – точка перегиба.