3.4. Выпуклость, вогнутость функции

 

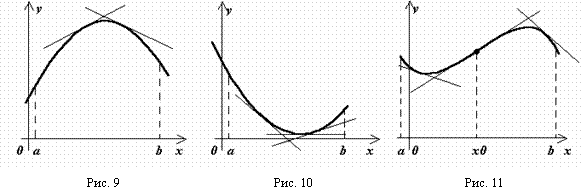
Определение. График функции f(x) называется выпуклым (рис. 9) на интервале (a, b) (вогнутым (рис. 10) на интервале (b, с)), если все точки графика расположены ниже (выше) любой его касательной на этом интервале.

Теорема 1. Если функция f(x) дважды дифференцируема на интервале и во всех его точках , то ее график вогнут (выпуклый) на этом интервале.

Определение. Точкой перегиба графика функции называется точка этого графика, которая отделяет выпуклую его часть от вогнутой (рис. 11).

Теорема 2. Пусть функция f(x) определена в некоторой окрестности точки b и дважды дифференцируема в ней всюду, кроме, быть может самой точки b. Тогда, если при переходе через точку b вторая производная меняет знак, то точка b есть точка перегиба графика функции.

 

Теорема 3. Если вторая производная функции  в точке b равна нулю ,то точка b – точка перегиба графика функции.

Алгоритм определения точек перегиба:

Шаг 1. Найти и точки х, в которых  или не существует, а  график функции f(x) непрерывен и которые лежат внутри области его расположения.

Шаг 2. Определить знак слева и справа от каждой из этих точек. Исследуемая точка х будет абсциссой точки перегиба, если по разные стороны от неё имеет разные знаки.

 

Пример 6. Определить направление выпуклости и точки перегиба кривой

Решение. Ищем точки х, в которых  или не существует, а кривая непрерывна и которые лежат внутри области расположения кривой:

в точках х = 0, х = 1. Эти точки являются искомыми, так как область расположения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как  существует всюду.

Исследуем найденные точки, определяя знак второй производной слева и справа от каждой из них. Запишем это исследование в табл. 2:

                                                                                                 Таблица 2

х	-1	0	1/2	1	10
	-	0	-	0	+
у	выпукла	нет перегиба	выпукла	перегиб	вогнута

Из табл. 2 следует, что х = 1 есть абсцисса точки перегиба кривой: у(1) = 2. Поскольку эта кривая непрерывная, то во всем интервале (-, 1) она выпукла, а во всем интервале (1, +) – вогнута.

Исходя, из определения унимодальной функции и направления выпуклости функции можно утверждать, что:

1)        если унимодальная функция выпукла, то она имеет глобальный максимум;

2)        если унимодальная функция вогнута, то она имеет глобальный минимум.

 

3.4. Критерий оптимальности

 

При анализе задач возникают два общих вопроса:

1)      Вопрос анализа в «статике». Как определить, представляет ли данная точка х* оптимальное решение задачи?

2)      Вопрос анализа в «динамике». Если х* не является точкой оптимума, то какая последовательность действий приводит к получению оптимального решения?

В этом разделе основное внимание уделяется решению вопроса анализа «в статике», а именно построению множества критериев оптимальности, позволяющих определить, является ли данное решение оптимальным.

Определение. Функция f(x), определенная на множестве S, достигает своего глобального минимума в точке х**S в том и только в том случае, если

f(x**)  f(x) для всех х  S.

Определение. Функция f(x), определенная на множестве S, имеет локальный минимум в точке х*  S в том и только в том случае, если f(x*)  f(x) для всех х, удаленных от х*

на расстояние, меньшее , то есть если существует >0 такое, что для любых х, удовлетворяющих условию /х-х*/<, выполняется неравенство f(x*)  f(x).

 

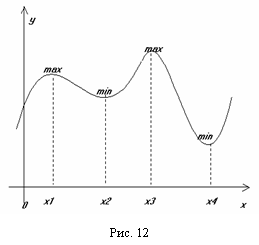
Пример 7. Рассмотрим график некоторой функции y = f(x) (рис. 12). Тогда имеем:

х₁ – точка локального максимума;

х₂ – точка локального минимума;

х₃ – точка глобального максимума;

х₄ – точка глобального минимума.