2 Этап. Безусловная оптимизация.

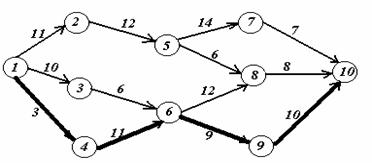
На этапе условной оптимизации получено, что минимальные затраты на перевозку груза из пункта 1 в пункт 10 составляют F₄(1)=33. Данный результат достигается при движении груза из 1-го пункта в 4-й. По данным таблицы четвертого шага необходимо двигаться в пункт 6, затем – в пункт 9 (см. таблицу второго шага) и из него – в конечный пункт (см. таблицу первого шага). Таким образом, оптимальный маршрут доставки груза: 1 4  6  9  10. На графе жирными стрелками показан оптимальный путь.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1.      Васильков Ю.В. Компьютерные технологии вычислений в математическом моделировании/ Ю.В. Васильков, Н.Н. Василькова – М.: Финансы и статистика, 2002.

2.      Геминтерн В. И., Каган Б. М. Методы оптимального проектирования. – М.: Энергия, 1980.

3.      Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Ч. 1. – М.: Высш. шк., 1999.

4.      Сборник задач по математике для втузов. Методы оптимизации/ Под ред.            А.В. Ефимова – М.: Наука, 1990.

5.      Зайцев М.Г., Зайцева Н.В. Методические материалы по курсу «Высшая математика» для факультетов менеджмента и экономики. – М.: Международный Университет Бизнеса и Управления «Братья Карич», 1997.

6.      Замков О.О. Математические методы в экономике/ О.О. Замков,                 Ю.А. Черемных, А.В. Толстопятенко– М.: Дело и Сервис, 1999.

7.      Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высш. шк., 1966.

8.      Интрилигатор М. Математические методы оптимизации и экономическая теория. – М.: Прогресс, 1975.

9.      Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. – М.: Высш. шк., 1979.

10.    Колесников А.Н. Краткий курс математики для экономистов: Учеб. пособие. – М.: ИНФРА-М, 1998.

11.    Красс М.С. Математика для экономических специальностей. – М.: ИНФРА-М, 1999.

12.    Ланкастер К. Математическая экономика. – М.: Советское радио, 1972.

13.    Малыхин В.И. Математика в экономике: Учеб. пособие. – М.: ИНФРА-М, 2001.

14.    Реклетис Г. Оптимизация в технике/ Г. Реклетис, А. Рейвиндран, К. Рэгсдел– М.: Мир, 1986.

15.    Шуп Т. Решение инженерных задач на ЭВМ. – М.: Мир, 1982.