2 Этап. Безусловная оптимизация.
Определяем компоненты оптимальной стратегии.
1-й шаг. По данным табл. 56 максимальный доход при распределении 5 млн. р. между четырьмя предприятиями составляет: с1 = 5, F1(5) = 12,5. При этом первому предприятию нужно выделить u1* = 0 млн. р.
2-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий.
с2 = с1 – u1* = 5 – 0 = 5 млн. р.
По данным табл. 55 находим, что оптимальный вариант распределения денежных средств размером 5 млн. руб. между третьим и четвертым предприятиями составляет: F2(5)=12,5 при выделении второму предприятию u2* = 2 млн. р.
3-й шаг. Определяем величину средств, приходящуюся на долю третьего и четвертого предприятий:
с3 = с2 – u2* = 5 – 2 = 3 млн. р.
По данным табл. 55 находим:
F3(3) = 7 и u3* = 2 млн. р., либо возможен второй вариант F3(3) = 7 и u3* = 1 млн. р.
4-й шаг. Определяем величину средств, приходящуюся на долю четвертого и пятого предприятий. Рассмотрим последовательно два возможных варианта.
Вариант 1: с4 = с3 – u3* = 3 – 2 = 1 млн. р., F4(1) = 2 и u4* = 1 млн. р.
Вариант 2: с4 = с3 – u3* = 3 – 1 = 2 млн. р., F4(2) = 3 и u4* = 2 млн. р.
Таким образом, оптимальный план инвестирования предприятий:
,
либо
,
который обеспечит максимальный доход,
равный
F1(5) = J1(0) + J2(2) + J3(2) + J4(1) = 0+4.5+5+2=11.5 млн. р.,
F2(5) = J1(0) + J2(2) + J3(1) + J4(2) = 0+4.5+4+3=11.5 млн. р.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 2
|
|
|
|
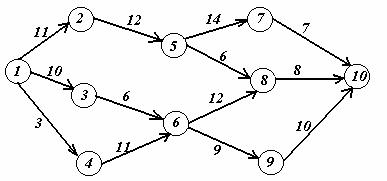
Задача. На заданной сети дорог имеется несколько маршрутов по доставке груза из пункта 1 в пункт 10. Стоимость перевозки единицы груза между отдельными пунктами сети проставлена у соответствующих ребер. Необходимо определить оптимальный маршрут доставки груза из пункта 1 в пункт 10, который обеспечил бы минимальные транспортные расходы.
Решение.1 этап. Условная оптимизация.
1-й шаг. k=1.
F1(i)=Ci10
На первом шаге в пункт 10 груз может быть доставлен из пунктов 7, 8 или 9.
Таблица 57
j i |
10 |
F1(i) |
j* |
7 |
7 |
7 |
10 |
8 |
8 |
8 |
10 |
9 |
10 |
10 |
10 |
2-й шаг. k=2.
Функциональное уравнение на втором шаге принимает вид
Все возможные перемещения груза на втором шаге и результаты расчета приведены в табл. 58.
Таблица 58
j i |
7 |
8 |
9 |
F2(i) |
j* |
5 |
14+7 |
6+8 |
- |
14 |
8 |
6 |
- |
12+8 |
9+10 |
19 |
9 |
3-й шаг. k=3.
Таблица 59
j i |
5 |
6 |
F3(i) |
j* |
2 |
12+14 |
- |
26 |
5 |
3 |
- |
6+19 |
25 |
6 |
4 |
- |
11+19 |
30 |
6 |
4-й шаг. k=4.
Таблица 60
j i |
2 |
3 |
4 |
F3(i) |
j* |
1 |
11+26 |
10+25 |
3+30 |
33 |
4 |