Пример выполнения задачи 4
Задача.
Минимизировать
при ограничении
Решение. Соответствующая задача безусловной оптимизации записывается в следующем виде:
минимизировать
Приравняв две компоненты градиента L к нулю, получим
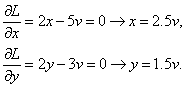
Для того чтобы проверить, соответствует ли стационарная точка x0 минимуму, вычислим элементы матрицы Гессе функции L(x; v), рассматриваемой как функция х,
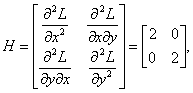
которая оказывается
положительно определенной. Это означает,
что L(x;
v)
– выпуклая функция х.
Следовательно, координаты
определяют
точку глобального
минимума.
Оптимальное значение v
находится путем подстановки значений
в
уравнение 5х
+ 3y
=9, откуда
52.5v
+31.5v
= 9 или v0
= 9/17. Таким
образом, условный минимум достигается
при x0
≈ 1,3235, y0
≈ 0,7941 и равен min
f(x)
= 2,3823.
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 3
Задача 1.
Вариант 1-8. Распределите оптимальным образом денежные средства величиной Х между N предприятиями. В результате выделения средств k-му предприятию в размере u оно дает доход Jk(u).
Вариант 1. X = 5 млн. р., N = 4. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(u), k = 1, …, 4, заданы табл. 38.
Таблица 38
u (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
J1(u) |
0 |
2 |
3 |
5,5 |
6,5 |
8 |
J2(u) |
0 |
4 |
5,5 |
7 |
9 |
10,5 |
J3(u) |
0 |
1 |
1,5 |
3 |
4 |
5 |
J4(u) |
0 |
4,5 |
5,5 |
7 |
8 |
9,5 |
Вариант 2. X = 5 млн. р., N = 5. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(u), k = 1, …, 4, заданы табл. 39.
Таблица 39
u (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
J1(u) |
0 |
1.5 |
2 |
3.5 |
5.5 |
9 |
J2(u) |
0 |
3 |
4.5 |
5.5 |
6.5 |
7.5 |
J3(u) |
0 |
4 |
5 |
5.5 |
6 |
9 |
J4(u) |
0 |
2 |
3 |
4 |
6.5 |
8 |
J5(u) |
0 |
3 |
4.5 |
6 |
7.5 |
3.5 |
Вариант 3. X = 100 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 25 тыс. р., но не могут превосходить 50 тыс. р. Функции Jk(u), k = 1, …, 4, заданы табл. 40.
Таблица 40
u (млн. р.) |
0 |
25 |
50 |
75 |
100 |
J1(u) |
0 |
12 |
14 |
20 |
28 |
J2(u) |
0 |
12 |
18 |
24 |
30 |
J3(u) |
0 |
12 |
16 |
24 |
30 |
J4(u) |
0 |
8 |
12 |
16 |
24 |
Вариант 4. X = 400 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 20 тыс. р., но не могут превосходить 200 тыс. р. Функции Jk(u), k = 1, …, 4, заданы табл. 41.
Таблица 41
u (млн. р.) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
J1(u) |
0 |
10 |
20 |
40 |
100 |
160 |
180 |
190 |
200 |
210 |
215 |
J2(u) |
0 |
20 |
40 |
60 |
80 |
95 |
101 |
102 |
103 |
104 |
105 |
J3(u) |
0 |
5 |
10 |
15 |
25 |
37 |
69 |
140 |
225 |
280 |
300 |
J4(u) |
0 |
30 |
68 |
95 |
140 |
160 |
170 |
175 |
176 |
177 |
178 |
Вариант 5. X = 5 млн. р., N = 4. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(u), k = 1, …, 4, заданы табл. 42.
Таблица 42
u (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
J1(u) |
0 |
3.5 |
4 |
5.5 |
7.5 |
11 |
J2(u) |
0 |
5 |
6.5 |
7.5 |
8.5 |
9.5 |
J3(u) |
0 |
6 |
7 |
7.5 |
8 |
11 |
J4(u) |
0 |
4 |
5 |
6 |
8.5 |
10 |
Вариант 6. X = 5 млн. р., N = 5. Средства предприятиям распределяются в количествах, кратных 1 млн. р. Функции Jk(u), k = 1, …, 4, заданы табл. 43.
Таблица 43
u (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
J1(u) |
0 |
4.5 |
6 |
7.5 |
9.5 |
13 |
J2(u) |
0 |
7 |
8.5 |
9.5 |
10.5 |
11.5 |
J3(u) |
0 |
4 |
9 |
9.5 |
10 |
13 |
J4(u) |
0 |
6 |
7 |
8 |
10.5 |
12 |
J5(u) |
0 |
7 |
8.5 |
10 |
11.5 |
7.5 |
Вариант 7. X = 100 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 25 тыс. р., но не могут превосходить 50 тыс. р. Функции Jk(u), k = 1, …, 4, заданы табл. 44.
Таблица 44
u (млн. р.) |
0 |
25 |
50 |
75 |
100 |
J1(u) |
0 |
18 |
20 |
26 |
34 |
J2(u) |
0 |
18 |
24 |
30 |
36 |
J3(u) |
0 |
18 |
22 |
30 |
36 |
J4(u) |
0 |
14 |
18 |
22 |
30 |
Вариант 8. X = 400 тыс. р., N = 4. Средства предприятиям распределяются в количествах, кратных 20 тыс. р., но не могут превосходить 200 тыс. р. Функции Jk(u), k = 1, …, 4, заданы табл. 45.
Таблица 45
u (млн. р.) |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
J1(u) |
0 |
20 |
30 |
50 |
110 |
170 |
190 |
200 |
210 |
220 |
225 |
J2(u) |
0 |
30 |
50 |
70 |
90 |
105 |
111 |
112 |
113 |
114 |
115 |
J3(u) |
0 |
15 |
20 |
25 |
35 |
47 |
79 |
150 |
235 |
290 |
310 |
J4(u) |
0 |
40 |
78 |
105 |
150 |
170 |
180 |
185 |
186 |
187 |
188 |
Вариант 9-11. Распределите оптимальным образом денежные средства инвестора величиной Х между четырьмя предприятиями. От выделенной суммы зависит прирост выпуска продукции на предприятиях, значения которых приведены в табл. 46, 47, 48.
Вариант 9.
Таблица 46
Денежные средства, Х |
Прирост выпуска продукции на предприятиях |
||||||||
1 |
2 |
3 |
4 |
||||||
20 |
9 |
11 |
13 |
12 |
|
||||
40 |
17 |
33 |
29 |
35 |
|
||||
60 |
28 |
45 |
38 |
40 |
|
||||
80 |
38 |
51 |
49 |
54 |
|
||||
100 |
46 |
68 |
61 |
73 |
|
||||
120 |
68 |
80 |
81 |
92 |
|
||||
Вариант 10.
Таблица 47
Денежные средства, Х |
Прирост выпуска продукции на предприятиях |
|||
1 |
2 |
3 |
4 |
|
20 |
13 |
15 |
17 |
16 |
40 |
21 |
37 |
33 |
39 |
60 |
32 |
49 |
42 |
44 |
80 |
42 |
55 |
53 |
58 |
100 |
50 |
72 |
65 |
77 |
120 |
72 |
84 |
85 |
96 |
Вариант 11.
Таблица 48
Денежные средства, Х |
Прирост выпуска продукции на предприятиях |
|||
1 |
2 |
3 |
4 |
|
40 |
8 |
6 |
3 |
4 |
80 |
10 |
9 |
4 |
6 |
120 |
11 |
11 |
7 |
8 |
160 |
12 |
13 |
11 |
13 |
200 |
18 |
15 |
18 |
16 |
Вариант 12-13. На развитие трех предприятий выделено 5 млн. р. Известна эффективность капитальных вложений в каждое предприятие, заданная значением нелинейной функции gi(xi) представленной в табл. 49. Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход. Распределение средств осуществляется в целых числах.
Вариант 12.
Таблица 49
-
х
g1
g2
g3
0
0
0
0
1
5.2
5
5.8
2
6
6.2
8.4
3
7.1
7.8
9.4
4
8.2
9.2
9.6
5
8.9
9.4
9.9
Вариант 13.
Таблица 50
-
х
g1
g2
g3
0
0
0
0
1
4.6
4.4
5.2
2
5.4
5.6
7.8
3
6.5
7.2
8.8
4
7.6
8.6
9
5
8.3
8.8
9.3
Вариант 14-20. Планируется деятельность двух предприятий в течение n лет. Начальные средства составляют s0. Средства х, вложенные в предприятие 1, приносят к концу года доход f1(x) и возвращаются в размере 1(х); аналогично, средства х, вложенные в предприятие 2, дают доход f2(x) и возвращаются в размере 2(х). По истечении года все оставшиеся средства заново перераспределяются между предприятиями 1 и 2, новых средств не поступает и доход в производство не вкладывается.
Требуется найти оптимальный способ распределения имеющихся средств.
Таблица 51
номер варианта |
s0 |
n |
f1(x) |
1(х) |
f2(x) |
2(х) |
14. |
300 |
4 |
0.6x |
0.4x |
0.3x |
0.7x |
15. |
300 |
3 |
0.7x |
0.8x |
0.2x |
0.3x |
16. |
200 |
4 |
0.3x |
0.8x |
0.4x |
0.5x |
17. |
10000 |
4 |
0.4x |
0.5x |
0.3x |
0.8x |
18. |
10000 |
4 |
0.5x |
0.8x |
0.6x |
0.7x |
19. |
600 |
3 |
0.4x |
0.5x |
0.3x |
0.8x |
20. |
600 |
4 |
0.6x |
0.4x |
0.3x |
0.7x |
Задача 2. На заданной сети дорог имеется несколько маршрутов по доставке груза из пункта 1 в пункт 10. Стоимость перевозки единицы груза между отдельными пунктами сети проставлена у соответствующих ребер. Необходимо определить оптимальный маршрут доставки груза из пункта 1 в пункт 10, который обеспечил бы минимальные транспортные расходы.
Вариант 1.
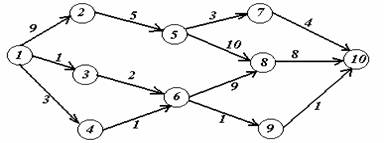
В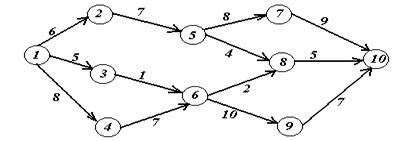
ариант
2.
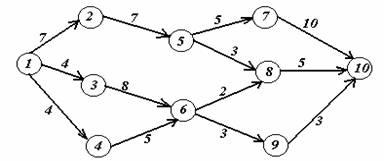
Вариант 3.
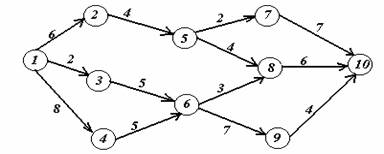
Вариант 4.
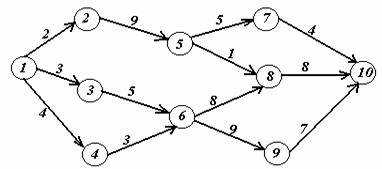
Вариант 5.
Вариант 6.
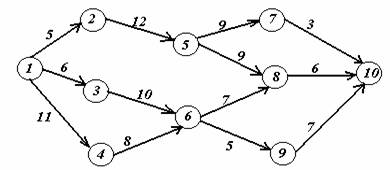
Вариант 7.
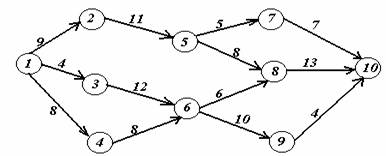
Вариант 8.
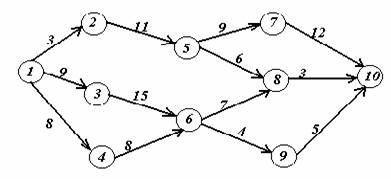
Вариант 9.
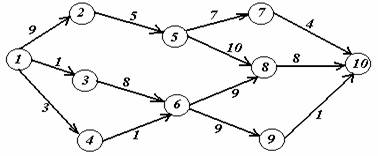
Вариант 10.
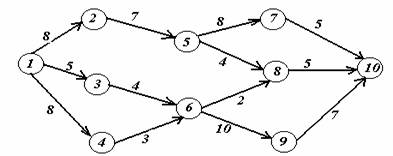
Вариант 11.
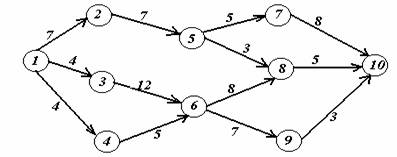
Вариант 12.
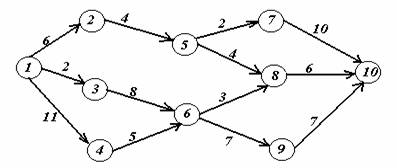
Вариант 13.
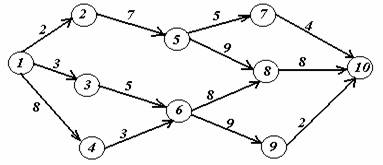
Вариант 14.
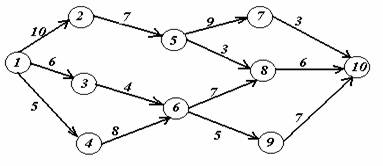
Вариант 15.
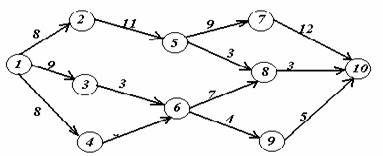
Вариант 16.
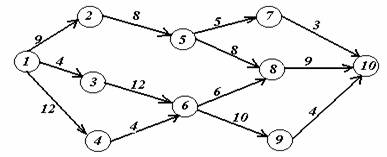
Вариант 17.
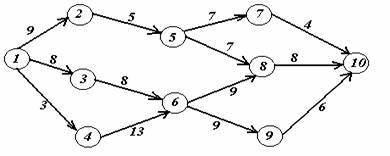
Вариант 18.
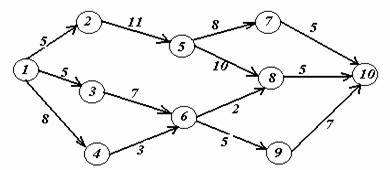
В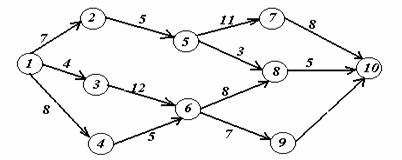
ариант
19.
Вариант 20.
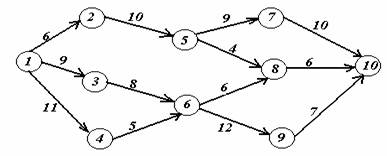
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 1
Задача 1.1. Планируется деятельность двух предприятий в течение 4 лет. Начальные средства составляют s0 = 700. Средства х, вложенные в предприятие 1, приносят к концу года доход f1(x)=0,7х и возвращаются в размере 1(х)=0,4х; аналогично, средства х, вложенные в предприятие 2, дают доход f2(x)=0,8х и возвращаются в размере 2(х)=0,5х. По истечении года все оставшиеся средства заново перераспределяются между предприятиями 1 и 2, новых средств не поступает и доход в производство не вкладывается.
Требуется найти оптимальный способ распределения имеющихся средств.
Решение. Уравнение состояний sk = 1(xk) + 2(sk-1 – xk) примет вид: sk = 0.4xk+0.5(sk-1-xk) или sk = 0.5sk-1-0.1xk.
Целевая функция k-го шага: 0.7xk+0.8(sk-1-xk)=-0.1xk+0.8sk-1.
Целевая функция
задачи:
Функциональные уравнения (уравнения Беллмана):
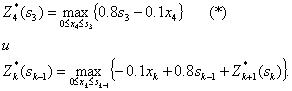
Далее проводим условную оптимизацию.
|
|
|
|
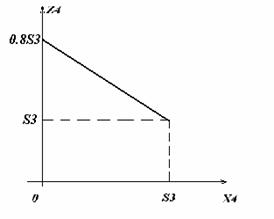
4-й шаг. Используем уравнение (*). Обозначим через Z4 функцию, стоящую в скобках, Z4 = -0.1x4+0.8s3; функция Z4 – линейная убывающая, так как угловой коэффициент -0,1 меньше нуля. Поэтому максимум достигается на конце интервала [0, s3] (см. рисунок).
Следовательно, Z4* = 0.8s3 при X4* =0.
3-й шаг. Уравнение
Находим s3 из уравнений состояний: s3 = 0.5s2-0.1x3 и, подставив его выражение в правую часть уравнения, получаем:
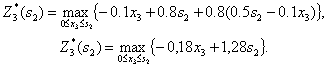
Как и в предыдущем случае, максимум достигается при x3 = 0; т. е. Z3*=1.2s2 при X3*=0.
2-й шаг. Из уравнения состояний: s2 = 0.5s1-0.1x2, поэтому первое функциональное уравнение при k=2 примет вид:
Линейная относительно x2 функция Z2* = 1.4s1-0.22x2 убывает на отрезке [0, s1], и поэтому ее максимум достигается при х2 = 0.
При этом: Z2* = 1.4s1, при X2* = 0.
1-й шаг. s1 = 0.5 s0-0.1x1. Первое функциональное уравнение при k=1 имеет вид:
Как и в предыдущем случае, максимум достигается в начале отрезка, т. е.: Z1*=1.5s0 при X1*=0.
На этом условная оптимизация заканчивается. Используя ее результат и исходные данные, получаем:
Zmax = Z1*(700), Zmax =1050.
Далее:
X1* = 0, Y1* = s0 = 700
(все средства выделяются второй отрасли)
s1* = 0.5700-0.10 = 350 X2* = 0, Y2* = s1 = 350
(все средства выделяются второй отрасли)
s2* = 0.5350-0.10 = 175 X3* =0 , Y3* = 175
(все средства выделяются второй отрасли)
s3* = 0.56400-0.10 = 87,5 X4* = 0, Y4* = 87,5
(все средства выделяются второй отрасли).
Оптимальная прибыль за 4 года, полученная от двух отраслей производства при начальных средствах 700 ед., равна 1050 ед. при условии, что первая отрасль получает по годам (0; 0; 0; 0), а вторая отрасль соответственно (700; 350; 175; 87,5).
Задача 1.2. Распределите оптимальным образом денежные средства величиной 5 млн. р. между 4 предприятиями. В результате выделения средств k-му предприятию в размере u оно дает доход Jk(u).
Таблица 52
u (млн. р.) |
0 |
1 |
2 |
3 |
4 |
5 |
J1(u) |
0 |
1.5 |
2 |
3.5 |
5.5 |
9 |
J2(u) |
0 |
3 |
4.5 |
5.5 |
6.5 |
7.5 |
J3(u) |
0 |
4 |
5 |
5.5 |
6 |
9 |
J4(u) |
0 |
2 |
3 |
4 |
6.5 |
8 |
Решение. Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах ui = {0, 1, 2, 3, 4, 5} млн. р.