Пример выполнения задачи 1

Задача. Найти минимальное значение f* и точку минимума х* функции  методом Пауэлла. Точку х* найти с точностью =0,1.

Решение. Пусть начальная точка x₁ =1 и длина шага x = 1. Для проверки на окончание поиска используем условие:

Итерация 1.

Шаг 1.

Шаг 2.

Шаг 3.

Шаг 4.

 

Шаг 5. Используя метод параболической аппроксимации, находим

 

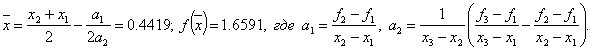
Шаг 6. Проверка на окончание поиска:

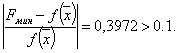
Продолжаем поиск.

 

Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки  в естественном порядке  Переходим к итерации 2, которая начинается с шага 4.

Итерация 2.

Шаг 4.

 

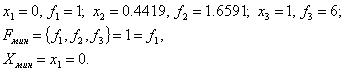
Шаг 5.

Шаг 6. Проверка на окончание поиска:

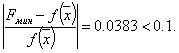
Условия окончания поиска выполняются, следовательно, вычисления заканчиваем.

Получили

 

Пример выполнения задачи 2

Задача. В предыдущей задаче выделить интервал, содержащий минимум функции так, чтобы концы интервала были целыми числами, и найти минимум той же функции с заданной точностью методом золотого сечения.

Решение. В предыдущей задаче функция  имеет минимум на интервале [0; 1]. Уточним его методом золотого сечения с точностью =0,1.

Первоначальные значения х₁ и х₂ находим по формулам

погрешность вычисляется по формуле   

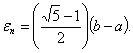
Вычисления представим в табл. 37.

Таблица 37

n	n	an	бn	х1(n)	x2(n)	f(x1(n))	f(x2(n))	Примечание
1	0,618	0	1	0,382	0,618	1,4965	2,3262
2	0,3819	0	0,618	0,2361	0,382	1,1988	1,4965
3	0,2361	0	0,382	0,1459	0,2361	1,0791	1,1988
4	0,1459	0	0,236	0,0901	0,1459	1,0311	1,0791
5	0,0902	0	0,146		0,0902		1,0311

 

Следовательно, х* 0,0902, и  f*  1,0311.

 

Пример выполнения задачи 3

Задача. Минимизировать функцию  методом наискорейшего спуска, заканчивая вычисления при

Решение. Найдем частные производные:

1-й шаг. Положим х⁽⁰⁾ = (0, 0), тогда

Для нахождения точки минимума функции Ф₀(h) используем метод Пауэлла. Поскольку шаг h изменяется в пределах 0 < h < 1, то за первоначальное значение примем      h = 0,  а h = 0.5. Таким образом, находим h₀ = 0.2.

Значит, х⁽¹⁾ =(0, 0) – 0.2(1, -1) = (-0.2, 0.2).

Вычислим значение производных: f(-0.2, 0.2) = (0.4, 0.4). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

2-й шаг. Составим функцию:

Снова используем метод Пауэлла, полагая h = 0 и h = 0.5, находим h₁ = 0.3.

Значит, х⁽²⁾ =(-0.2,0.2) – 0.3(0.4,-0.4) = (-0.32, 0.08).

Вычислим значение производных: f(-0.32, 0.08) = (0.28, -0.2). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

3-й шаг. Составим функцию:

Используем метод Пауэлла, полагая h = 0 и h = 0.5, находим h₂ = 0.2327.

Значит, х⁽³⁾ =(-0.32-0,23270,28; 0.08+0.23270.2)=(-0.3852; 0.1265). Вычислим значение производных: f(х⁽³⁾) = (0.1031, 0.1442). Условия завершения поиска не выполняются, поэтому переходим к следующему шагу.

4-й шаг. Составим функцию:

Используем метод Пауэлла, полагая h = 0 и h = 0.5, находим h₂ = 0.27.

Значит, х⁽⁴⁾ =(-0.3852-0,270,1031; 0.1265-0.270.1442)=(-0.413; 0.0876). Вычислим значение производных: f(х⁽⁴⁾) = (0.0864, -0.0614). Условия завершения поиска  выполняются,  поэтому требуемая точность достигнута и