Вопросы к главе 2

 

1.        Что такое параметры плана?

2.        Приведите пример параметров плана.

3.        Дайте определение целевой функции.

4.        Как изображается целевая функция?

 

Глава 3. Функция одной переменной

 

Задача оптимизации, в которой характеристическая мера задана функцией одной переменной, относится к наиболее простому типу оптимизационных задач. Тем не менее, анализ задач такого типа занимает центральное место в оптимизационных исследованиях как теоретической, так и практической направленности. Обычно решаются именно такие задачи или они используются для анализа подзадач, ориентированных на решение многомерных задач оптимизации. Важность теоретических и прикладных оптимизационных задач с одной управляемой переменной обусловила разработку большого числа алгоритмов их решения. Вспомним некоторые определения и свойства, связанные с понятием функции одной переменной.

 

3.1. Определение функции одной переменной и её свойства

 

Повторим понятия функции и её свойства, которые нам потребуются для дальнейшего изложения материала.

Определение. Функция f(x) представляет собой правило, которое позволяет каждому значению хХ поставить в соответствие единственное значение y = f(x)У, где х – независимая переменная (аргумент), y – зависимая переменная (значение функции). Говорят, что функция f имеет область определения D(f)=X и область значений R(f)Y.

Определение. Множество пар {(x, f(x)): xD(f)} называется графиком функции f.

Существует три основных способа задания функции:

      при аналитическом способе задания функции зависимость между переменными определяется формулой;

      при табличном способе задания функции выписываются в определенном порядке значения аргумента и соответствующие значения функции;

      при графическом способе задания функции зависимость между переменными отражается с помощью графика.

Рассмотрим некоторые функциональные зависимости, используемые в экономике:

      функция спроса – зависимость спроса D на некоторый товар от его цены p;

      функция предложения – зависимость предложения S некоторого товара от его цены p;

      функция полезности – субъективная числовая оценка данным индивидом полезности и и количества х товара для него;

      функция издержек – зависимость издержек I на производство х единиц продукции;

      налоговая ставка – зависимость налоговой ставки N в процентах от величины годового дохода Q.

Все эти функции, кроме последней, весьма трудно выразить аналитически. При необходимости их находят путем кропотливого анализа. Последняя же функция, напротив, обычно довольно хорошо известна всему обществу и законодательно утверждена.

Определение. Функция f(x) имеет предел b, когда х стремится к а, если значения f(x) сколь угодно близко приближаются к числу b, когда значения переменной х сколь угодно близко приближаются к числу а.

Обозначение. .

Следует отметить, что в этом определении рассматриваются значения х, сколь угодно близкие к числу а, но не совпадающие с а.

Определение. Если функция f(x) определена в точке а и выполняется равенство , то f(x) называется непрерывной функцией в точке а.

Определение. Функция, непрерывная в каждой точке своей области определения, называется непрерывной функцией. В противном случае функцию называют разрывной.

График непрерывной функции можно начертить без отрыва руки.

Непрерывные функции обладают следующими свойствами:

      сумма или произведение непрерывных функций является непрерывной функцией;

      отношение двух непрерывных функций является функцией непрерывной во всех точках, в которых знаменатель отношения не обращается в нуль.

Замечание. Метод, эффективный при анализе непрерывных функций, может оказаться неэффективным при исследовании разрывных функций, хотя обратное не исключается.

Определение. Функция f(x) называется возрастающей (убывающей) на множестве X, если из того, что x₁<x₂ вытекает, что f(x₁)<f(x₂) (f(x₁)>f(x₂)). Функция f(x) называется неубывающей (невозрастающей) на множестве X, если из того, что x₁ x₂, x₁, x₂ X вытекает, что f(x₁) f(x₂) ( f(x₁) f(x₂)).

Теорема. Пусть функция f(x) дифференцируема на интервале (a, b). Тогда:

      если первая производная функции всюду на этом интервале, то функция возрастает на нем;

      если первая производная  всюду на этом интервале, то функция убывает;

      первая производная всюду на этом интервале, то функция постоянна на этом интервале.

Определение. Возрастающие, убывающие, неубывающие, невозрастающие функции называются монотонными.

Замечание. Монотонная функция не обязательно должна быть непрерывной.

Пример 1. Найти интервалы монотонности функции  f(x)=(1-x²)³.

Решение. Находим производную:  Решим уравнение . Получим х₁=0, х₂=1, х₃=-1. Функция f(x) определена и непрерывна на всей числовой оси. Поэтому точки х₁, х₂, х₃ являются критическими точками. Других критических точек нет, так как  существует всюду.

Исследуем критические точки, определяя знак  слева и справа от каждой этой точки. Для сокращения вычислений и для наглядности это исследование удобно записать в виде табл. 1:

   Таблица 1

х	-2	-1	-1/2	0	1/2	1	2
	+	0	+	0	-	0	-
f(x)	возр.		возр.		убыв.		убыв.

 

В первой строке помещены все критические точки в порядке расположения их на числовой оси; между ними вставлены промежуточные точки, расположенные слева и справа от критических точек. Во второй строке помещены знаки производной в указанных промежуточных точках. В третьей строке – заключение о поведении функции на исследуемых интервалах. На интервале (-; 0) функция возрастает, на интервале           (0; +) функция убывает.

Определение. Функция f(x) является унимодальной на отрезке [a, b] в том и только в том случае, если она монотонна по обе стороны от единственной на рассматриваемом интервале оптимальной точки х*.

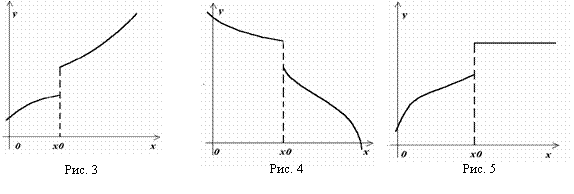
Пример 2. Приведем примеры графиков унимодальных функций:

      на рис. 6 непрерывная функция;

      на рис. 7 – разрывная функция;

      на рис. 8 – дискретная функция.

Множество функций, унимодальных на отрезке [a; b], будем обозначать Q[a; b].

Для проверки унимодальности функции f(x) на практике обычно используют следующие критерии:

1)        если функция f(x) дифференцируема на отрезке [a; b]  и производная не убывает на этом отрезке, то f(x)Q[a; b];

2)        если функция f(x) дважды дифференцируема на отрезке [a; b] и при х[a; b], то f(x)Q[a; b].

Пример 3. Показать, что функция унимодальна на отрезке [3; 5].

Решение. Найдем последовательно первую и вторую производные функции:

Решим уравнение . Корни полученного квадратного трехчлена х₁=2 и х₂=3. Следовательно, и, в частности, при х [3; 5]. Используя второй критерий унимодальности, получаем, что f(x)Q[3; 5].

Пример 4. Выяснить, является ли функция f(x)=x²-3x+xlnx на отрезке [1;2] унимодальной.

Решение. Найдем первую и вторую производные функции:

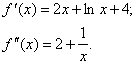
Решим уравнение . Полученное уравнение имеет единственный корень х=-0,5. Следовательно, если х-0,5 и, в частности, при х[1; 2]. Используя второй критерий унимодальности, получаем, что f(x)Q[1; 2].

Определение. Рассмотрим множество SR. Мы можем определить соответствие, с помощью которого каждой точке xS приписывается единственное числовой значение. Такое соответствие называется скалярной функцией f, определенной на множестве S.

Определение. В теории оптимизации f называется целевой функцией, а S – допустимой областью, множеством точек, удовлетворяющих ограничениям, или областью допустимых значений х.