Пример выполнения задачи 4

Задача. Найти градиент функции в точке М(1; -3) и найти производную в той же точке по направлению MN, если N(0; -5).

Решение. а) Находим частные производные:  и их значения в точке М(1; -3):

б) Найдем единичный вектор l, имеющий данное направление:

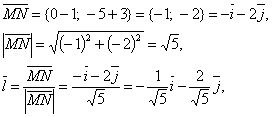
откуда

Вычислим частные производные функции в точке М(1; -3):

Получаем,

 

Пример выполнения задачи 5

Задача. Исследовать функцию  на локальный экстремум.

Решение. Найдем частные производные функции z и приравняем их к нулю:

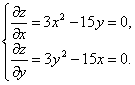
Её решением являются пары (0; 0) и , т.е. на экстремум надо проверить точки М₀(0; 0) и М₁ . Частные производные второго порядка имеют вид:

Вычислим D в точках М₀ и М₁:

 значит экстремума в точке М₀ нет;

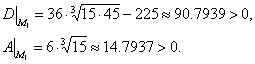
Так как в точке М₁ коэффициенты D>0 и A>0, то точка М₁ является точкой минимума.

Расчетно-графическое задание 2

 

Задача 1. Методом Пауэлла найти точку минимума х* функции f(x) с точностью  и минимум f*.

1.        

2.        

3.        

4.        

5.        

6.        

7.        

8.        

9.        

10.    

11.    

12.    

13.    

14.    

15.    

16.    

17.    

18.    

19.    

20.    

 

Задача 2. В предыдущей задаче выделить интервал, содержащий минимум функции, так, чтобы концы интервала были целыми числами, и найти минимум той же функции с заданной точностью методом золотого сечения.

 

Задача 3. Минимизировать функцию методом наискорейшего спуска, заканчивая вычисления при

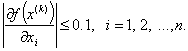
1.     

2.     

3.     

4.     

5.     

6.     

7.     

8.     

1.     

2.     

3.     

4.     

5.     

6.     

7.     

8.     

9.     

10. 

11. 

12. 

 

Задача 4. Найти глобальное решение задачи методом Лагранжа:

Таблица 36

номер варианта	a	б	c
	2	3	7
	1	5	8
	3	1	6
	2	4	9
	4	1	6
	2	5	6
	1	4	8
	3	5	7
	4	3	6
	1	6	9
	3	1	10
	1	5	10
	2	7	10
	4	4	8
	4	2	12
	6	2	4
	6	2	8
	8	2	5
	8	2	10
	8	3	11