Пример выполнения задачи 1

Задача. Найти точки локального экстремума функции и значения функции в них:

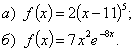
Решение. а) Находим производную:

Решим уравнение х=11.

Функция f(x) определена и непрерывна на всей числовой оси. Поэтому точка х=11 является критической точкой. Других критических точек нет, так как существует всюду.

Исследуем критическую точку, определяя знак первой производной, слева и справа от неё.

Таблица 33

x	0	11	20
	+	0	+
f(x)	возрастает		возрастает

Так как на всей числовой оси функция возрастает, то она не имеет экстремумов.

б) Находим производную:

Решим уравнение

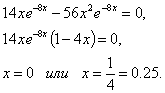
Функция f(x) определена и непрерывна на всей числовой оси. Поэтому точки х₁=0 и х₂=0,25 являются критическими точками. Других критических точек нет, так как f(x) существует всюду. Исследуем критические точки, определяя знак первой производной, слева и справа от каждой точки.

Таблица 34

x	-1	0	0.1	0.25	1
	-	0	+	0	-
f (x)	убывает		возрастает		убывает

На интервале (0; 0,25) функция возрастает, а на интервалах (-; 0) и (0,25; +) – убывает.

Значит, х₁=0 – точка минимума, f(0)=0; х₂=0,25 – точка максимума, f(0.25)0.0596.

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 2

Задача. Найти наибольшее и наименьшее значения функции на интервале [-0.9; 2.2].

Решение. Найдем критические точки функции f(x), лежащие внутри заданного отрезка: , при х₁=0 и х₂=-1/3. Эти точки лежат внутри рассматриваемого отрезка и являются критическими. Вычислим значения функции на концах отрезка и в критических точках:

f(-0.9)=9.732; f(-1/3) 12.1296; f(0)=12; f(2.2) 103.476.

Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции f(x) на отрезке [-0.9; 2.2] равно 103,476 и достигается на правой границе отрезка х=2,2, а её наименьшее значение равно 9,732 и достигается на левой границе отрезка х=-0,9.

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 3

Задача. Найти точки перегиба, промежутки выпуклости и вогнутости функции