Вопросы к главе 1
1. Почему необходимо использование математики в экономике?
2. Что такое математическая модель?
3. Как строится математическая модель экономического явления и объекта? Приведите пример построения модели.
4. Что такое оптимизация?
5. Какие существуют методы оптимизации?
6. Какие экономические задачи решаются методами оптимизации?
Глава 2. Основы теории оптимизации
Термином «оптимизация» обозначают процесс, позволяющий получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего, или «оптимального», решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. Поэтому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.
Рассматривая некоторую произвольную систему, описываемую m уравнениями с n неизвестными, можно выделить три основных типа задач:
если m = n, то задачу называют алгебраической. Такая задача обычно имеет единственное решение;
если m > n, то задача переопределена, как правило, не имеет решений;
если m < n, то задача недоопределена, имеет бесконечно много решений.
В практике чаще всего приходится иметь дело с задачами третьего типа.
Введем ряд определений.
2.1. Параметры плана
Определение. Параметры плана – это независимые переменные параметры, которые полностью и однозначно определяют решаемую задачу.
Это неизвестные величины, значения которых вычисляются в процессе оптимизации. В качестве проектных параметров могут служить любые основные или производные величины, служащие для количественного описания системы.
Например, в качестве параметров могут рассматриваться значения длины, массы, времени, температуры.
Число проектных параметров характеризует степень сложности данной задачи проектирования.
Обозначения. Обычно число проектных параметров обозначают через n, х – сами проектные параметры с соответствующими индексами
х1, х2, …, хn – n проектных параметров задачи.
2.2. Целевая функция (план)
Определение. Целевая функция – выражение, значение которого стремимся сделать максимальным или минимальным.
Целевая функция позволяет количественно сравнить два альтернативных решения. С математической точки зрения целевая функция описывает некоторую (n+1)-мерную поверхность.
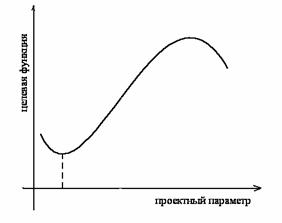
1) Если имеется только один проектный параметр, то целевую функцию можно представить кривой на плоскости (рис. 1).
2) Если проектных параметров два, то целевая функция будет изображаться поверхностью в пространстве трех измерений (рис. 2).
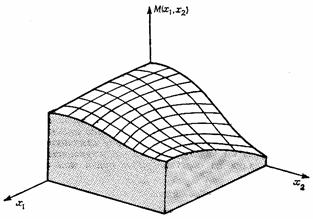
Определение. При трех и более проектных параметрах поверхности, задаваемые целевой функцией, называются гиперповерхностями и не поддаются изображению обычными средствами.
Целевая функция в ряде случаев может быть представлена:
кусочно-гладкой функцией;
таблицей;
только целыми значениями;
двумя значениями – да или нет (дискретная функция).
В каком бы виде ни была представлена целевая функция, она должна быть однозначной функцией проектных параметров.
В ряде задач оптимизации требуется введение более одной целевой функции. Иногда одна из них может оказаться несовместимой с другой. Примером служит проектирование самолетов, когда одновременно требуется обеспечить максимальную прочность, минимальный вес и минимальную стоимость. В таких случаях конструктор должен ввести систему приоритетов. В результате получается «функция компромисса», позволяющая в процессе оптимизации пользоваться одной составной целевой функцией.