6.3. Метод наискорейшего спуска

 

Основным недостатком градиентного метода является необходимость частого вычисления производных от функции f(х). Этого недостатка лишен метод наискорейшего спуска, который заключается в следующем.

В текущей точке вычисляется  grad f(x), и затем в направлении градиента ищется min f(x). Практически это может быть осуществлено любым методом одномерной оптимизации (поиск по одному направлению – направление градиента), наиболее часто используется сканирование до первого локального минимума по направлению grad f(x).

В результате вдали от оптимума эффективность метода повышается, мы быстрее попадем в район оптимума, в окрестности которого эффективность метода снижается из-за частой смены направления поиска и приближается к эффективности метода градиента.

В ряде случаев можно повысить скорость выхода в район оптимума предъявлением невысоких требований к точности поиска min по направлению (задается величиной h – шагом поиска по направлению). Условием окончания может являться малость модуля градиента  функции f(x): |grad f(x)| < . Можно также использовать и малость приращений по переменным в результате шага, но только в том случае, если на данном шаге мы «проскочили» оптимум, иначе может оказаться, что малость шага обусловлена не близостью к оптимуму, а малостью коэффициента пропорциональности шага h.

В ряде случаев используют уменьшение шага поиска оптимума по направлению после каждой смены направления. Условием окончания поиска в этом случае является достижение заданной малой величины шага.

Метод наискорейшего спуска отличается от градиентного спуска способом определения величины h_k, которая находится из условия:

                               (*)

Такой выбор h_k обеспечивает максимально возможное уменьшение функции f(x) вдоль направления ее антиградиента  в точке х^(k).

Таким образом, для определения h_k на каждом шаге метода наискорейшего спуска решается одномерная задача минимизации функции Ф_k(h), для чего можно использовать рассмотренные выше методы одномерной оптимизации.

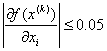Пример 64. Минимизировать функцию  методом наискорейшего спуска, завершив вычисления при , i = 1, 2.

Решение. Найдем частные производные:

1-й шаг. Положим х⁽⁰⁾ = (0, 0), тогда

Функцию Ф₀(h) находим, используя соотношение (*). Для нахождения точки минимума функции Ф₀(h) используем метод Пауэлла. Поскольку шаг h изменяется в пределах 0 < h < 1, то за первоначальное значение примем h = 0,  а h = 0.5. Таким образом находим h₀ = 0.22.

Значит, х⁽¹⁾ =(0, 0) – 0.22(1, 1) = (-0.22, -0.22).

Вычислим значение производных: f(-0.22, -0.22) = (0.204, -0.236). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

2-й шаг. Составим функцию:

Снова используем метод Пауэлла, полагая h = 0 и h = 0.5, находим h₁ = 0.32.

Значит, х⁽²⁾ =(-0.22,-0.22) – 0.32(0.204, -0.236) = (-0.2853, -0.1445).

Вычислим значение производных: f(-0.2853, -0.1445) = (0.08, 0.0726). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

3-й шаг. Составим функцию:

Используем метод Пауэлла, полагая h = 0 и h = 0.5, находим h₂ = 0.24.

Значит, х⁽³⁾ =(-0.2853-0.240.08, -0.1445-0.240.0726) = (-0.3045, -0.1619).

Вычислим значение производных: f(х⁽³⁾) = (0.0182, -0.0205). Условия завершения поиска выполняются, поэтому требуемая точность достигнута и

Пример 65. Минимизировать функцию f(x, y) = x³+2y²-3x-4y, методом градиентного спуска с дроблением шага, завершив вычисления при

Решение. Найдем частные производные:

1-й шаг. Положим х⁽⁰⁾ = (0, 0), тогда

Функцию Ф₀(h) находим, используя соотношение (*). Для нахождения точки минимума функции Ф₀(h) используем метод Пауэлла. Поскольку шаг h изменяется в пределах 0 < h < 1, то за первоначальное значение примем h = 0,  а h = 0.5. Таким образом находим h₀ = 0.281.

Значит, х⁽¹⁾ =(0, 0) – 0.281(-3, -4) = (0.843, 1.124).

Вычислим значение производных: f(х⁽¹⁾) = (-0.8681, 0.496). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

2-й шаг. Составим функцию:

Снова используем метод Пауэлла, полагая h = 0 и h = 0.5, находим h₁ = 0.2121.

Значит, х⁽²⁾ =(0.833+0.21210.8681, 1.124-0.21210.496) = (1.0171, 1.0188).

Вычислим значение производных: f( х⁽²⁾) = (0.1035, 0.0752). Условия завершения поиска не выполняются, следовательно, переходим к следующему шагу.

3-й шаг. Составим функцию:

Используем метод Пауэлла, полагая h = 0 и h = 0.5, находим h₂ = 0.2196.

Значит, х⁽³⁾ =(1.0171-0.21960.1035, 1.0188-0.21960.0752) = (0.9944, 1.002).

Вычислим значение производных: f(х⁽³⁾) = (-0.0335, 0.008). Условия завершения поиска выполняются, поэтому требуемая точность достигнута и