6.2. Метод градиентного спуска

Метод градиента в чистом виде формирует шаг по перемен­ным как функцию от градиента f(х) в текущей точке поиска. Про­стейший алгоритм поиска min f(x) записывается в векторной форме следующим образом:

или в скалярном виде:

Величина рабочего шага в направлении градиента h grad f(х) зависит от величины градиента, который заранее учесть трудно, и от коэффициента пропорциональности шага h, с помощью кото­рого можно управлять эффективностью метода.

Поиск каждой новой точки состоит из двух этапов:

1) оценка градиента f(x) путем вычисления частных произ­водных от f(х) по каждой переменной х_j;

2) рабочий шаг по всем переменным одновременно.

Величина h сильно влияет на эффективность метода. Большей эффективностью обладает вариант метода, когда шаг по каждой переменной определяется направляющими косинусами градиента

где

В этом случае величина рабочего шага не зависит от величи­ны модуля градиента, и ею легче управлять изменением h. В рай­оне оптимума может возникать значительное "рыскание", поэто­му используют различные алгоритмы коррекции h.

Наибольшее распространение получили следующие алгоритмы:

1)              (без коррекции);

2)            

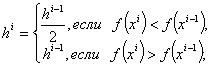
3)            

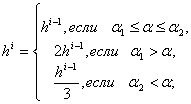
где  - угол между градиентами на предыдущем и текущем шаге; ₁ и ₂ – заданные пороговые значения выбираются субъективно (например, ₁=/6, ₂=/3).

Вдали от оптимума направление градиента меняется мало, поэтому шаг можно увеличить (второе выражение), вблизи от оптимума направление резко меняется (угол между градиентами f(x) большой), поэтому h сокращается (третье выражение).

Для оценки частных производных используются разностные методы:

          алгоритм с центральной пробой

          алгоритм с парными пробами

где g_i – пробный шаг по i-й переменной, выбираемый достаточно малым для разностной оценки производной.

Первый алгоритм требует меньших затрат по сравнению со вторым (обычно затраты выражаются количеством вычислений критерия оптимальности), но позволяет получить решение менее точно, чем второй, и эта погрешность зависит от величины проб­ного шага.

Условием окончания поиска может являться малость модуля градиента f(x), т. е. |gradf(x)| < .

Пример 60. Требуется найти минимум функции f(x, y) = x³+2y²-3x-4y, завершив вычисления при погрешности  = 0,01,  выбрав начальное приближение х⁽⁰⁾ = - 0,5  и у⁽⁰⁾ = -1,  коэффициент шага h = 0.1.

Решение. Необходимые начальные данные приведены в условии задачи. Для вычислений выберем работу с шагом без коррекции  (h = const).

Найдем частные производные функции:

Следовательно,

Значит,

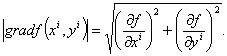
Переменные определяются по формулам:

Результаты вычислений занесем в табл. 17

Таблица 17

п	x	y	f(x, y)	df/dx	df/dy	|grad f|
1	2	3	4	5	6	7
1	-0,500	-1,000	7,3750	-2,2500	-8,0000	8,3104
2	-0,275	-0,200	1,6842	-2,7731	-4,8000	5,5435
3	0,002	0,280	-0,9701	-3,0000	-2,8800	4,1586
4	0,302	0,568	-2,5061	-2,7258	-1,7280	3,2274
5	0,575	0,741	-3,4003	-2,0085	-1,0368	2,2603

   Продолжение табл. 17

1	2	3	4	5	6	7
6	0,776	0,844	-3,8120	-1,1947	-0,6221	1,3469
7	0,895	0,907	-3,9508	-0,5958	-0,3732	0,7031
8	0,955	0,944	-3,9877	-0,2651	-0,2239	0,3471
9	0,981	0,966	-3,9967	-0,1111	-0,1344	0,1744
10	0,992	0,980	-3,9990	-0,0453	-0,0806	0,0925
11	0,997	0,988	-3,9997	-0,0183	-0,0484	0,0517
12	0,999	0,993	-3,9999	-0,0073	-0,0290	0,0299
13	1,000	0,996	-4,0000	-0,0029	-0,0174	0,0177
14	1,000	0,997	-4,0000	-0,0012	-0,0104	0,0105
15	1,000	0,998	-4,0000	-0,0005	-0,0063	0,0063

 

В последней точке модуль градиента меньше заданной погрешности

(0,0063 < 0.01), поэтому поиск прекращается.

Итак, и

Пример 61. Требуется найти минимум функции  завершив вычисления при погрешности  = 0,5,  выбрав начальное приближение х⁽⁰⁾ = 0  и у⁽⁰⁾ = 0,  коэффициент шага h = 0.1.

Решение. Необходимые начальные данные приведены в условии задачи. Для вычислений выберем работу с шагом без коррекции  (h = const).

Результаты вычислений занесем в табл. 18.

    Таблица 18

п	x1	x2	f(x1, x2)	df/d x1	df/d x2	|grad f|
1	0,0000	0,0000	1,0000	1,0000	1,0000	1,4142
2	-0,1000	-0,1000	0,8487	0,6187	0,4187	0,7471
3	-0,1619	-0,1419	0,8045	0,4143	0,1706	0,4480
4	-0,2033	-0,1589	0,7880	0,2895	0,0604	0,2957
5	-0,2323	-0,1650	0,7806	0,2077	0,0123	0,2080
6	-0,2530	-0,1662	0,7768	0,1515	-0,0072	0,1517
7	-0,2682	-0,1655	0,7748	0,1118	-0,0138	0,1126
8	-0,2794	-0,1641	0,7737	0,0831	-0,0146	0,0844
9	-0,2877	-0,1626	0,7731	0,0621	-0,0131	0,0635
10	-0,2939	-0,1613	0,7727	0,0466	-0,0110	0,0479

 

В последней точке модуль градиента меньше заданной погрешности, поэтому поиск прекращается.

Итак, и

Рассмотрим градиентный метод минимизации функции с дроблением шага.

Пусть f(x) выпуклая дифференцируемая во всем n-мерном пространстве функция и требуется найти её точку минимума х*. Выбрав произвольное начальное приближение , построим последовательность

                                                (9)

где величины h_k (параметрические шаги) выбираются достаточно малыми для того, чтобы выполнялось условие

                                                    (10)

В качестве условия окончания вычислений обычно используется близость к нулю градиента , т. е. выполнение неравенств

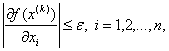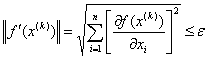или                        (11)

( - заданное достаточно малое число), после чего полагают

Если при некотором k условие (10) нарушается, то шаг h_k уменьшают (дробят) в заданное число раз до выполнения неравенства (10) и продолжают вычисления.

Пример 62. Минимизировать функцию методом градиентного спуска с дроблением шага, завершив вычисления при

Решение. Выбрав начальное приближение х⁽⁰⁾ = (0, 0) и h₀ = 1, построим последовательность (9), записывая результаты вычислений в табл. 19

Таблица 19

k			f(x(k))			hk		Примечание
0	0	0	1	1	1	1		Условие (10) нарушено. Уменьшаем h0 в 2 раза.
	-1	-1	3,1353	-	-
	0	0	1	1	1	0,5		Условие (10) нарушено. Уменьшаем h0 в 2 раза.
	-0,5	-0,5	1,118	-	-
1	0	0	1	1	1	0,25		Условие (10) выполнено
	-0,25	-0,25	0,794	0,1065	-0,3935	0,25	0,4077
2	-0,2766	-0,1516	0,7741	0,0984	0,0451	0,25	0,1082	Условие (10) выполнено
3	-0,3012	-0,1629	0,7725	0,0262	-0,023	0,25	0,0349	Точность достигнута(11)

 

Итак,

Пример 63. Минимизировать функцию f(x, y) = x³+2y²-3x-4y, методом градиентного спуска с дроблением шага, завершив вычисления при

Решение. Выбрав начальное приближение х⁽⁰⁾ = (-0.5, -1) и h₀ = 0.1, построим последовательность (9), записывая результаты вычислений в табл. 20.

Таблица 20

k	x	y	f(x, y)			hk		Примечание
1	2	3	4	5	6	7	8	9
1	-0,5000	-1,0000	7,3750	-2,2500	-8,0000	0,1
	-0,2750	-0,2000	1,6842	-2,7731	-4,8000	0,1	5,5435	Условие (10) выполнено
2	0,0023	0,2800	-0,9701	-3,0000	-2,8800	0,1	4,1586	Условие (10) выполнено

Продолжение табл. 20

1	2	3	4	5	6	7	8	9
3	0,3023	0,5680	-2,5061	-2,7258	-1,7280	0,1	3,2274	Условие (10) выполнено
4	0,5749	0,7408	-3,4003	-2,0085	-1,0368	0,1	2,2603	Условие (10) выполнено
5	0,7757	0,8445	-3,8120	-1,1947	-0,6221	0,1	1,3469	Условие (10) выполнено
6	0,8952	0,9067	-3,9508	-0,5958	-0,3732	0,1	0,7031	Условие (10) выполнено
7	0,9548	0,9440	-3,9877	-0,2651	-0,2239	0,1	0,3471	Условие (10) выполнено
8	0,9813	0,9664	-3,9967	-0,1111	-0,1344	0,1	0,1744	Условие (10) выполнено
9	0,9924	0,9798	-3,9990	-0,0453	-0,0806	0,1	0,0925	Условие (10) выполнено
10	0,9969	0,9879	-3,9997	-0,0183	-0,0484	0,1	0,0517	Условие (10) выполнено
11	0,9988	0,9927	-3,9999	-0,0073	-0,0290	0,1	0,0299	Точность достигнута(11)

 

Итак,