Вопросы к главе 5

 

1.    Дайте определение функции многих переменных.

2.    Приведите примеры функций многих переменных, используемых в экономике.

3.    Что называется графиком функции двух переменных? Приведите примеры.

4.    Сформулируйте определение множества (линии) уровня функции двух переменных. Может ли множество уровня функции двух переменных не быть линией?

5.    Опишите взаимосвязь между градиентом функции двух переменных и ее линией уровня.

6.    Перечислите основные свойства градиента функции.

7.    Дайте определение возрастающей (убывающей) функции многих переменных.

8.    В каком случае функция является вогнутой?

9.    Всегда ли локальный экстремум выпуклой функции является глобальным?

10.         Дайте определение экстремума функции двух переменных.

11.         Сформулируйте достаточные условия максимума и минимума функции двух переменных.

Глава 6. Многомерная безусловная градиентная оптимизация

 

6.1. Концепция методов

 

В данном разделе рассматриваются методы построения улучшающих последовательностей при отыскании экстремума функции R(x) без активных ограничений.

Определение. Активными называют ограничения, на границе которых находится решение.

Если известно, что решение лежит строго внутри допустимой области, например, в случае ограничений типа неравенств, то такие ограничения лучше выводить из задачи на этапе её постановки.

Замечание. Ограничения типа равенств всегда активные.

Величина шага х в рекуррентном соотношении

вычисляется с использованием градиента целевой функции R(x), т. е.

,

при этом шаг может определяться с использованием градиента в одной (текущей) или в двух (текущей и предыдущей) точках. На­правление градиента, как известно, показывает направления наискорейшего возрас­тания функции, а его модуль — скорость это­го возрастания.

Для решения задачи безусловной минимизации функции многих переменных наиболее часто применяют приближенные методы, в основе которых лежит вычисление производных функций первого порядка. Такие методы обычно называют градиентными.

Рассмотрим простой пример. Представим себе, что альпинисту завязали глаза и сказали, что он должен добраться до вершины «унимодальной» горы. Даже ничего не видя, он может это сделать, если все время будет двигаться вверх. Хотя любая ведущая вверх тропа, в конечном счете, приведет его к вершине, кратчайшей из  них будет самая крутая, если, правда, альпинист не натолкнется на вертикальный обрыв, который придется обходить. (Математическим эквивалентом обрыва на поверхности, образуемой целевой функцией, являются те ее места, где поставлены условные ограничения). Предположим пока, что задача оптимизации не содержит ограничений. Позднее мы включим их в схему поиска.

В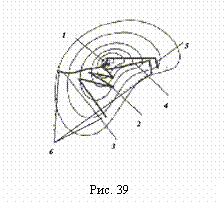 отличие от других рассмотренных выше вычислительных мето­дов поисковые методы оптимизации содержат неформально (т.е. субъ­ективно) задаваемые па­раметры, которые су­щественно влияют на эффективность поиска, вследствие чего один и тот же метод может дать совершенно различные траектории поиска. По­этому для всех методов, рассматриваемых далее, на рис. 39  приводится лишь одна из возможных траекторий: 1 – оптимум; 2 – траектория метода градиента; 3 – траектория метода тяжелого шарика; 4 – траектория метода наискорейшего спуска; 5 – траектория метода сопряженных градиентов; 6 – начальные точки траектории. Кроме того, для всех приве­денных траекторий выбраны различные начальные условия, с тем, чтобы не загромождать построения. На этом и последующих ри­сунках зависимость R(х_1, х₂) приведена в виде линий уровня на плоскости в координатах х₁ - х₂.