5.8. Экстремум функции многих переменных

Рассмотрим вопрос анализа «в статике» с использованием положений линейной алгебры и дифференциального исчисления, а также условий, которые позволяют идентифицировать точки оптимума. Такие условия используются для проверки выбранных точек и дают возможность выяснить, являются ли точки точками минимума, максимума или седловыми точками.

Определение. Экстремумом функции двух переменных называется её максимальное или минимальное значение на заданном множестве изменения переменных.

Экстремумы и методы их нахождения имеют широкое применение в экономических исследованиях, при выборе наилучших вариантов инвестиций, производственных программ, вложения денег в покупки и т. п.

Определение. Значение функции f(M) в точке М₀ называется максимумом (минимумом), если оно является набольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках:

.

Пример 53. На рис. 37 представлен график функции двух переменных, точка М₀(5, 8), в которой достигается максимум функции, окрестность точки М₀(5, 8), максимальное значение функции f(x, y), равное f(5, 8); на рис. 38 – график функции точка  М₀(4, 9), в которой достигается минимум функции, окрестность точки М₀(4, 9), минимальное значение функции f(4, 9).

Из определения экстремума функции видно, что понятие экстремума является локальным. Другими словами, можно сказать, что приведенное определение экстремума является определением локального экстремума, функция может иметь несколько локальных максимумов или минимумов. Ясно, что при нахождении лучшего решения следует ориентироваться на наибольший из локальных максимумов, если ищется наибольшее значение функции, и на наименьший из локальных минимумов, если ищется наименьшее значение функции.

Определение. Наибольшая величина из локальных максимумов называется глобальным максимумом, наименьший из локальных минимумов – глобальным минимумом.

Задача нахождения локальных экстремумов, а тем более глобальных, для функции нескольких переменных является достаточно трудной, в общем случае для произвольного числа переменных практически неразрешимой. Для выпуклых функций разработаны специальные методы нахождения экстремумов.

Замечание. Любой локальный экстремум выпуклой функции является глобальным.

Определение. Функция многих переменных может иметь максимум или минимум (экстремум) только в точках, лежащих внутри области определения функции, в которых все ее частные производные первого порядка равны нулю или не существуют. Такие точки называются критическими.

Замечание. Это необходимые условия экстремума, но недостаточные, они могут выполняться и в точках, где нет экстремума.

Это определение дает схему нахождения экстремальных точек. Составляется система уравнений относительно переменных х и у:

Решение системы представляет собой пары (х₀, у₀), (х₁, у₁) и т.д., которые называются точками «подозрительными» на экстремум, т. е., если функция имеет экстремумы, то они могут достигаться только в этих точках. Для определения, достигается ли в каждой из найденных точек максимальное (минимальное) значение или в рассматриваемой точке нет экстремума, требуется проведение дополнительных исследований.

Пример 54. Найти экстремум функции z = x² + (y – 1)².

Найдя частные производные и приравняв их к нулю, получаем систему уравнений:

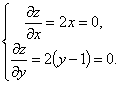
Решение этой системы очевидно: х = 0, у = 1. Поскольку z  0 при всех х, у, то ясно, что найденная точка (0, 1) есть точка минимума.

Пример 55. Определить, имеет ли функция z = x³ + y³ экстремумы.

Решение. Найдем частные производные и приравняем их к нулю:

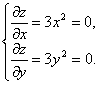
Точка (0, 0) является «подозрительной». Однако экстремума функция в этой точке не имеет, так как в любой окрестности этой точки она принимает значения разных знаков, а в самой точке (0, 0) значение функции равно нулю.

Рассмотрим достаточные условия экстремума для функции двух переменных.

Пусть функция z = f(x, y) непрерывна со своими частными производными первого и второго порядка в некоторой окрестности точки М(х₀, у₀). Пусть в этой точке выполнены необходимые условия экстремума:

В этой точке пусть вычислены частные производные второго порядка.

Введем обозначения:

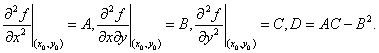
Тогда достаточные условия максимума и минимума имеют вид:

1)        если D>0, то в точке М функция f(x, y) имеет экстремум, а именно, максимум при A<0 и минимум при A>0;

2)        если D<0, то в точке М функция f(x, y) экстремума не имеет;

3)        если D = 0, то требуются дополнительные исследования.

Пример 56. Исследовать на экстремум функцию: z = f(x, y) = x³ + y³ – 3xy.

Решение. Составим систему уравнений:

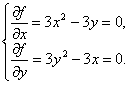
Её решением являются пары (0, 0) и (1, 1), т. е. на экстремум надо проверить точки М₀(0, 0) и М₁(1, 1). Частные производные второго порядка имеют вид:

Вычислим D в точках М₀ и  М₁ :  < 0, значит экстремума в этой точке нет; > 0, при этом А = 6 > 0 и, следовательно, в точке М₁ – минимум.

Пример 57. Исследовать на экстремум функцию

Решение. Ищем критические точки:

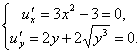
Находим М₀(1, 0) и М₁(-1, 0). Эти точки принадлежат области определения исследуемой функции: - < x < +, 0  y < + (которая представляет половину плоскости хОу, лежащую выше оси Ох, включая и ось Ох), но они расположены не внутри этой области, а на её границе у = 0. Поэтому точки М₀ и М₁ не являются критическими. Частные производные по х и по у существуют во всей области определения функции u. Поэтому данная функция, как не имеющая критических точек, не имеет экстремума.

Пример 58. Исследовать на экстремум функцию

Решение. Ищем критические точки:

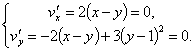
Решая систему, найдем единственную критическую точку функции М(1; 1).

Далее, чтобы установить, будет ли экстремум в точке М, вычисляем

Здесь оказалось, что D = 0. Чтобы установить, имеет ли экстремум функция v в критической точке М, исследуем знак её приращения

 вблизи точки М.

Пусть М₁ лежит на биссектрисе у = х. Тогда  Если М₁ будет ниже М, т.е. если у_М1 < 1, то < 0, а если М₁ будет выше М, т.е. если у_М1 > 1, то > 0. Здесь оказалось, что вблизи точки М разность не сохраняет знака, вследствие чего в точке М нет экстремума.

Замечание. Для функций с числом переменных больше двух достаточные условия экстремума имеют сложный вид и требуют глубоких знаний по математическому анализу

Пример 59. Исследовать на экстремум функцию

Решение. Ищем критические точки:

Эти частные производные не обращаются в нуль ни при каких значениях x, y, z; они не существуют (обращаются в бесконечность) в точке М(0, 0, 0). Эта точка лежит внутри области определения функции w, которая представляет совокупность всех точек (x, y, z) пространства. Поэтому М(0, 0, 0) критическая точка.

Исследуя знак разности вблизи точки М, убеждаемся, что при любых отличных от нуля значениях х, y, z она сохраняет положительный знак. Поэтому М есть точка минимума,