5.3. Экономический смысл частных производных

 

Рассмотрим в качестве примера производственную функцию Кобба—Дугласа:

у = АК^L^,

 где А,   — неотрицательные кон­станты и   1; а К — объем фондов либо в стоимостном выра­жении, либо в натуральном количестве, скажем число станков; L - объем трудовых ресурсов, например число рабочих; у — выпуск про­дукции в стоимостном выражении.

Величину l = у/L естественно назвать средней производитель­ностью труда — ведь это количество продукции (в стоимостном вы­ражении), произведенное одним рабочим.

Величину k = у/К естественно назвать средней фондоотдачей — ведь это количество продукции (в стоимостном выражении), прихо­дящееся на один станок (на одну единицу фондов).

Величину f = К/L естественно назвать средней фондовооруженностью или просто фондовооруженностью — ведь это стоимость фон­дов, приходящаяся в среднем на единицу трудовых ресурсов, напри­мер на одного рабочего.

С другой стороны, зафиксируем текущее состояние предприя­тия, т.е. объем фондов К и число рабочих L. Им соответствует выпуск продукции у = у(К, L). Если нанять еще одного рабочего, то прира­щение выпуска составит y=y(K, L+1)-y(K, L). Это частное приращение и потому , а так как L=1, то .

Вывод: Частная производная от производственной функции по объему трудовых ресурсов (кратко: производная выпуска по тру­ду) приблизительно равна добавочной стоимости продукции, производная   называется предельной произво­дительностью произ­веденной еще одним дополнительным рабочим. По этой причине эта частная  труда.

Если же увеличить фонды еще на единицу — купить еще один cтанок, то добавочная стоимость продукции, произведенной на нем, окажется приблизительно равной частной производной от производ­ственной функции по объему фондов (кратко: производной выпуска по фондам). Эта частная производная  называется пре­дельной фондоотдачей.

И предельная производительность труда, и предельная фондоотдача — это абсолютные величины. Но в экономике чрезвычайно удобно задавать такие вопросы: на сколько процентов изменится вы­пуск продукции, если число рабочих увеличится на 1%, или если фонды возрастут на 1%? и т.д. В таких вопросах и ответах на них ис­пользуется  понятие «эластичность функции по аргументу» или «отно­сительная производная».

 

5.3. Частные производные высших порядков

 

Функцию многих аргументов u=f(x₁, …, х_n) можно дифференцировать по каждому аргументу. Полученные частные производные (первого порядка) обычно зависят от тех же аргументов и каждую из них также можно дифференцировать по каждому аргументу.

Определение. Частные производные от частных производных первого порядка называются частными производными второго порядка.

О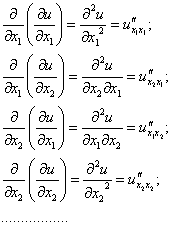 бозначение.

 

 

 

 

 

 

 

 

 

Определение. Частные производные от частных производных второго порядка называются частными производными третьего порядка.

Аналогично определяются и обозначаются частные производные четвертого, пятого и других высших порядков.

Замечание. Частные производные высших порядков, отличающиеся только последовательностью дифференцирования, равны, если они непрерывны.

Частные производные высших порядков находятся путем последовательного нахождения одной производной вслед за другой по правилам дифференцирования функции одной переменной.

Пример 40. Найти частные производные второго порядка функции

Решение. Сначала находим частные производные первого порядка, затем искомые частные производные второго порядка: