5.3. Частные производные функции многих переменных

 

Возрастание (убывание) функции показывает тенденцию изменения функции: функция возрастает (убывает), если с ростом переменной значения функции увеличиваются (уменьшаются). Количественное измерение этих изменений происходит путем вычислений приращений абсолютных, относительных, предельных.

Определение. Абсолютным приращением функции f(x, y) по переменной х называется разность:

Ясно, что если , то функция на этом промежутке возрастает по х, если , то убывает.

Определение. Абсолютным приращением функции f(x, y) по переменной у называется разность:

Определение. Под приращением функции понимают разность:

где точки (х₁, у₁) и (х₂, у₂) из области определения функции.

Определение. Относительное приращение определяется как приращение в расчете на единицу изменения переменной х или переменной у.

Относительное изменение по переменной х рассчитывается как отношение:

по переменной у:

Пример 35. Пусть дана линейная функция z=f(x, y)= - 2x – 2y + 20.

Рассчитаем прирост функции по х при переходе из точки (2; 1) в точку (4; 1), т. е. в случае, когда приращение по х равно 2:

Итак, приращение функции равно –4, т. е. функция х на интервале изменения переменной х(2, 4) убывает.

Относительное приращение равно:

Пример 36. Пусть дана функция: z=f(x, y)=2x²y+4y².

Прирост функции в точке (2, 3) по переменной у при у=0,5 составляет:

т. е. по переменной у функция возрастает.

Относительное приращение равно:

Рассмотрим прирост функции по переменной у в точке (2, 4) при у=0,5:

Таким образом, можно заметить, что величина приращения разная для разных у, хотя переменная х и у одинаковы.

По аналогии с функцией одной переменной определяется непрерывность функции двух переменных.

Определение. Функция f(x, y) называется непрерывной в точке (х, у), если приращение функции f стремится к нулю при х0 и у0, т. е., если выполняется условие:

.

Для функций многих переменных, как и в случае функции одной переменной, изучаются предельные значения относительных приращений по отдельным переменным. Так, по переменной х рассматривается:

 или  при х0.

 

Определение. Если существует предел отношения  при х0, то он называется частной производной первого порядка функции f(x, y) по х.

Частная производная по х (у) показывает предельное приращение функции в данной точке (х, у) при  фиксированном у (х).

Анализ предельных изменений функций имеет широкое применение в экономических исследованиях. Например, равенства предельных доходов и предельных затрат, равенства

удельных предельных полезностей по товарам являются достаточными условиями эффективности принимаемых решений и др.

Функцию u=f(x₁, …, х_n) можно дифференцировать по каждому из ее аргументов, считая при этом все остальные аргументы постоянными.

Рассмотрим еще одно определение частной производной.

Определение. Производная от функции u=f(x₁, …, х_n) по х₁, взятая в предположении, что все остальные аргументы x₂, …, х_n являются постоянными, называется частной производной от u  по x₁ и обозначается   или .

Аналогично определяются и обозначаются частные производные от функции u по каждому из остальных ее аргументов.

Частные производные функции многих переменных находятся по известным правилам дифференцирования функции одной независимой переменной.

Пример 37. Найти частные производные от функции

Решение. Считая z функцией только одного аргумента х, находим

Аналогично, считая z функцией только у, получим

Пример 38. Найти частные производные от функции u(x₁, x₂, x₃)=sin²(3x₁+2x₂-x₃).

Решение. Считая х₂ и х₃ постоянными, рассмотрим функцию u как функцию одной переменной х₁:

Аналогично находим производные по х₂ и по х₃:

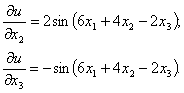
Пример 39. Найти частные производные функции

Решение.