4.2.1. Метод параболической аппроксимации

 

Метод заключается в замене нелинейной функции f(x) квадратичной параболой f₂(x), построенной по трем точкам, принадлежащим f(x), с последующим нахождением максимума (минимума) параболической функции, используя аналитические условия оптимальности:

На первом этапе в качестве исходных трех точек используется

В этих точках вычисляется f(x) и по полученным точкам f(x₁), f(x₂), f(x₃) строится парабола

коэффициенты которой находятся из решения соответствующей системы уравнений:

Условие оптимальности приводит к уравнению

где х₄ – точка максимума (минимума) параболы f₂(x). Далее выбирается новый отрезок, внутри которого находится точка х₄, и, используя х₃, х₄, строится новая парабола, по которой уточняется положение максимума (минимума) f(x) и т. д. До тех пор, пока величина отрезка, внутри которого находится оптимум, не будет меньше заданной погрешности . Таким образом, метод имеет итерационный характер.

К достоинству метода относится высокая скорость сходимости, хотя метод может не всегда сходится.

На рис. 19 рассмотрена ситуация, когда метод параболической аппроксимации сходится к решению уже на третьем этапе. Парабола, построенная по точкам х₃, х₄, х₅, практически совпадает с исходной функцией. На рис. 20 парабола не имеет максимума уже на втором этапе. В первом случае решение найти можно, во втором – нельзя.

Пример 19. Дана функция f(x) = sin (x + 1). Найти максимум на интервале  [-1; 2], точность  = 0,01.

Решение. Для построения аппроксимирующей параболы находим точки  В первом случае система уравнений для нахождения коэффициентов параболы примет вид:

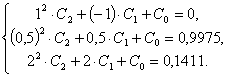
Решение системы можно найти любым из известных способов, например, по формулам Крамера. На первом шаге получаем = 0,5571, f( ) = 0.9999. По этой точке, а также по второй и третьей исходным точкам, лежащим по обе стороны от точки максимума параболы, аналогично строится вторая парабола.

                                                                                                            Таблица 14

п	x1	x2	x3	f(х1)	f(x2)	f(x3)	C2	C1	C0
1	-1	0.5	2	0	0.9975	0.1411	-0.412	0.459	0.871	0.5571	0.9999
2	0.5	0.5571	2	0.9975	0.9999	0.1411	-0.4249	0.4914	0.858	0.5782	1
3	0.5571	0.5782	2	0.9999	1	0,1411	-0,4208	0.4809	0.8626	0.5714	1
4	0,5571	0,5714	0,5782	0,9999	1	1	-0,5	0,5708	0,8371	0,5708	1

 

Поскольку уже на третьем шаге разница между двумя точками максимума менее заданной погрешности, то поиск можно заканчивать (четвертый шаг присутствует для наглядности вычислений). Поэтому х* 0,5708, и  f*  f (0,5708) = 1.

Для реализации данного метода существует ещё один подход.

Если задана последовательность точек х₁, х₂, х₃ и известны соответствующие этим точкам значения функции f₁, f₂, f₃, то можно определить постоянные величины  а₀, а₁, а₂ таким образом, что значения квадратичной функции

совпадут со значениями f(x) в трех указанных точках. Перейдем к вычислению q(x) в каждой из трех заданных точек. Прежде всего, так как

Поскольку

Наконец, при   х = х₃

Разрешая последнее уравнение относительно а₂, получаем

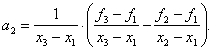
Таким образом, по трем заданным точкам и соответствующим значениям функции можно оценить параметры аппроксимирующего квадратичного полинома достаточно высоко, значит, в соответствии с предложенной стратегией поиска построенный полином можно использовать для оценивания координаты точки оптимума. Напомним, что стационарные точки функции одной переменной определяются путем приравнивания к нулю ее первой производной и последующего нахождения корней полученного таким образом уравнения. В данном случае из уравнения

можно получить

Поскольку функция f(x) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина  окажется приемлемой оценкой координаты точки истинного оптимума х*.

Видно, что оба подхода отличаются друг от друга только способом вычисления коэффициентов (в первом случае - C₀, C₁, C₂; во втором - а₀, а₁, а₂) квадратичного полинома. Результаты при этом нисколько ни отличаются. Легко убедиться, что для практических вычислений удобнее использовать формулы

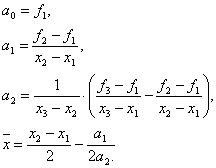
Пример 20. Найти минимальное значение f* и точку минимума х* функции на отрезке [1.5; 2]. Точку х* найти с точностью =0,05.

Решение. Значения  х₁, х₂, х₃ находим также как и в предыдущем примере.

                                                                                                                                                                Таблица 15

п	x1	x2	x3	f1	f2	f3	а0	а1	а2
1	1,5	1,75	2	-89,4375	-92,1211	-88	-89,4375	-10,7344	54,4375	1,7236	-92,1346
2	1,5	1,7236	1,75	-89,4375	-92,1346	-92,1211	-89,4375	-12,0623	50,2988	1,7317	-92,1384

Уже после второго шага можно закончить вычисления, так как заданная точность достигнута (1,7317-1,7236 = 0,0081 <  = 0,05).

Значит, х* 1,7317, и  f*  f (1,7317) = -92,1384.

Пример 21. Найти точку минимума х* функции  на отрезке [0.5; 1] с точностью =0,05.

Решение. Вычисления представим в виде табл. 16:

                                                                                                            Таблица 16

 

п	x1	x2	x3	f1	f2	f3	а0	а1	а2
1	0,5	0,75	1	-3,5907	-2,4389	-0,5	-3,5907	4,6075	6,296	0,2591	-3,5328
2	0,2591	0,5	1	-3,5328	-3,5907	-0,5	-3,5328	-0,2404	8,6677	0,3934	-3,7475
3	0,3934	0,5	1	-3,7475	-3,5907	-0,5	-3,7475	1,4708	7,7657	0,352	-3,7373

 

Точность достигнута (0,3934 – 0,352 = 0,414 <  = 0,05).

Значит, х* 0,352, и  f*  f (0,352) = -3,7373.